Misfit Dislocations in Heterojunctions

Calculating the critical thickness of a layer with lattice constant a₁ on top of a substrate with lattice constant a₂ can become rather involved, if all components contributing to the elastic energy are taken into account.

In particular, you may want to consider the anisotropy of the situation, the effect of a finite thickness of the top layer, the real geometry with respect to the dislocations (their line energy depends on this and that, and they may be split into partial dislocations).

Then, after arriving at a formula, you may chose to make all kinds of approximations.

In the backbone part of the script we had a simple formula (taken from a paper of the very well known scientist Sir Peter Hirsch) which you can find in the link (together with some comments):

d_crit =	=	b 8 · p · f · (1 + n)	· ln	e · d_crit r₀

With b = Burgers vector of the dislocations; usually somewhat smaller than a lattice constant, f = misfit parameter = (a₁ - a₂)/a₁, n = Poisson ration » 0,4, e = really e = base of natural logarithms r₀ = inner core radius of the dislocation; again in the order of lattice constant.

Lets look at some other approaches

A formula taking into account most everything going back to J. W. Matthews and A.E. Blakeslee (1974) , who pioneered this field of research, is

d_crit	=	b · (1 – n ) · cos²Q 8 · p · (1 + n) · f · cosl	·	æ ç è	ln	æ è	d_crit b	ö ø	+ 1	ö ÷ ø

with Q = angle between the dislocation line and its Burgers vector, l = angle between the slip direction and that line in the interface plane that is normal to the line of intersection between the slip plane and the interface.

For simple systems (Q = 90^o and l = 0^o), we have

d_crit	=	b 8 · p · f · (1 + n)	·	æ ç è	ln	æ è	d_crit r₀	ö ø	+ 1	ö ÷ ø

And that is Sir Peters equation if you insert ln(e) for the 1 in the ln term.

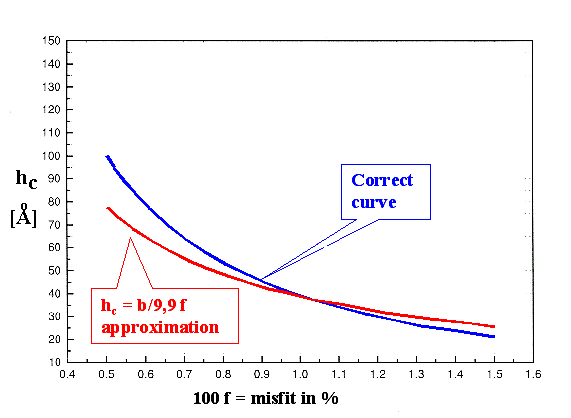
While Sir Peter used the simple approximation

d_crit	»	b 6f

the comparison with the (computer-generated) correct functional dependence suggests

d_crit	»	b 9f

which is a bit different!

A plot of the full formula and the approximation looks like this:

Critical thickness fOr misfit dislOcatiOn free interfaces

Similar curves are contained in the books of Mayer and Lau or Tu, Mayer and Feldmann; they supposedly use the same equation but show rather different results.

Well, somewhere should be a mistake (maybe I made one?). In any case, it nicely demonstrates the point made in the backbone section: Do not blindly believe a theory. In case of doubt, try it out.

With frame

5.3.3 Real Heterojunctions