|
Let's first look at an ideal single quantum well
(SQW), rectangular and with an extension dz and infinite walls (the index "z"
serves to remind us that we always have a three-dimensional system with the one-dimensional quantum structures along the
z-axis). |
|
 |
We have already solved the Schrödinger equation for this problem: It is
nothing else but the one-dimensional free electron gas with dz instead of the length L
of the crystal used before. |
|
 |
We thus can take over the solutions for the energy levels; but being much wiser now, we use
the effective mass instead of the real mass for the electrons
and obtain |
| |
| E | = |
(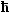 · kz)2 · kz)2
2mz* |
|
|
|
 |
With kz = ± nz · 2 p/dz,
and n = ± (0,1,2,3,...). |
|
 |
We have used periodic boundary conditions for this case,
which is physically sensible for large crystals. The wave functions are propagating plane waves in this case. It is, however,
more common and sensible to use fixed boundary conditions, especially for small dimensions. The wave functions then are
standing waves. Both boundary conditions produce identical results for energies, density of states and so on, but the set
of wave vectors and quantum numbers are different; we have |
|
 |
kz = jz· p/dz,
and j = 1,2,3,.. (we use j as quantum number to indicate a change in the system). For the energy
levels in a single quantum well we now have the somewhat modified formula |
| |
| E | = |
 2 · p 2 2 · p 2
2mz* |
· | j 2
dz2 |
|
|
 |
The absolute value of the energy levels and the spacing in between increases with
decreasing width of the SQW, i.e. with decreasing thickness dz of the small
band gap semiconductor sandwiched between the two large band gap semiconductors. |
|
 |
Large differences in energy levels might be useful for producing light with interesting wave
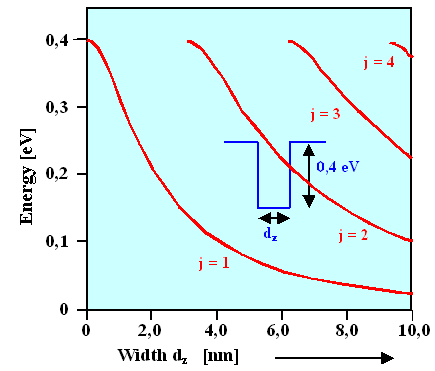
lengths. In infinitely deep ideal SQWs this is not a problem, but what do we get for real SQWs with a depth
below 1 eV? This needs more involved calculations, the result is shown in the following figure. |
| |
|
|
 |
The SQW has a depth of 0.4 eV; if it disappears for dz
= 0, we simply have a constant energy of 0.4 eV for the ground state; all excited states stop at that level. |
 |
For layer thicknesses in the nm region (which is technically accessible)
energy differences of 0.2 . . . 0.3 eV are possible, which are certainly interesting, but not so much for direct
technical use. |
|
 |
While SQWs are relatively easy to produce and provide a wealth of properties for research
(and applications), we will now turn to multiple quantum wells obtainable by periodic
stacking of different semiconductors as shown before. |
| | |
|
Energy Bands in Multiple Quantum Wells |
| | |
 |
Since single atoms may also be described as SQWs (for one electron you
just have the hydrogen atom type with a Coulomb potential), we must expect that the wave function of the electrons start
to overlap as soon as the single SQWs in the MQW structure are close enough. |
|
 |
The situation is completely analogous to the qualitative formation of a crystal
with a periodic potential from atoms. The discrete energy levels must split into many level, organized in bands. |
|
 |
This is exactly what happened; it was Leo Esaki
who first did the calculations (and more) for this case for which he was awarded the Nobel prize. |
|
 |
Her is the result for the same system shown above. |
| |
|
|
 |
Energy bands with respectable band gaps develop indeed, and we now should redraw the band
diagram from before to include this fact: |
| |
|
|
 |
We have "mini-bands" in the quantum wells (for symmetry reasons also for the holes
in the quantum well along the valence band); green denotes occupied levels; blue empty levels. |
 |
What do we gain by this (besides a Nobel prize)? |
|
 |
A structure that is used in commercially sold LASER diodes!
In other words, quite crucial parts of the information technology rely on MQWs. |
|
 |
We will come back to this issue in the context of semiconductor lasers. |
| | |
|
© H. Föll (Semiconductors - Script)