 |
The free electron gas model works with
a constant potential. This is, of course, a doubtful approximation; essentially
only justified because it works – up to a point. |
|
 |
Approximations:
Constant potential U = U0 = 0 within a crystal with length L in all directions;
only one electron is considered. |
|
 |
The true potential outside the crystal will turn out to be irrelevant
due to periodic boundary conditions (see below). |
 |
The major formulas and interpretations needed are: |
 |
Time independent one-dimensional Schrödinger equation :
|
| |
| – |
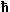 2 2
2me |
æ
ç
è |
¶2y(x,y,z)
¶ x2 | + |
¶ 2y(x,y,z)
¶ y2 | + |
¶
2y (x,y,z)
¶
z2 | ö
÷
ø |
+ U(r) · y(x,y,z
) | = |
E · y(x,y,z) | | |
| | |
| | |
| | = 0 |
| |
|
|
|
 |
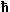 = h "bar" =
h/2p = Plancks constant/2p = h "bar" =
h/2p = Plancks constant/2p
me
= electron mass
y = wave function
E = total energy = kinetic energy + potential energy. Here it is identical to the kinetic energy because the potential energy is zero. |
 |
Potential
U( x) as defined above; i.e. U(x) = U0 = const = 0 for 0 £ x £ L. (Remember that L
is the macroscopic size of the crystal.) |
|
 |
For the (potential) energy, there is always a free choice of zero point; here it is convenient
to put the bottom of the potential well at zero potential energy. We will, however, change that later on. |
 |
Boundary conditions: Several
choices are possible! Here, we use periodic conditions
(also called Born–von
Karman conditions), leading to a so-called supercell: |
|
|
 |
Solution (for 3-dimensional case)
|
| |
|
|
| y | = |
æ
ç
è |
1
L |
ö
÷
ø | 3/2 |
· | exp (i · k · r) |
|
| |
| r | = |
position vector |
| | = | (x, y, z) | | |
| |
| k |
= |
wavevector |
| | = |
(kx, ky, kz) | | |
| | | kx | = |
±
nx · 2 p/L | | ky |
= | ±
ny · 2p /L | | kz |
= | ±
nz · 2p/L | | | |
| | nx , ny, nz |
= | quantum numbers | | | = |
0, 1, 2, 3, ... | | | | |
| i | = | (–1)1/2 |
|
|
|
 |
A somewhat more general form for crystals
with unequal sides can be found in the link. |
 |
There are infinitely many solutions, and every individual solution is selected
or described by a set of the three quantum numbers nx , ny, nz
. The solution y describes a plane
wave with amplitude (1/L)3/2
moving in the direction of the wave vector
k . |
 |
Next, we extract related quantities of interest in connection with moving particles or waves: |
|
 |
The wavelength
l
of the "electron wave" is given by |
| |
|
|
 |
The momentum p of the electron is given by |
| |
| p | = |
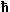 · k · k |
|
|
|
 |
From this and with m = electron mass we obtain the velocity
v of the electron to be |
| |
| v | = |
p
me | = |
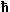 · k · k
me |
|
|
 |
The numbers nx, ny, n z are
quantum numbers ; their values (together with the value
of the spin) are characteristic
for one particular solution of the Schrödinger equation of the system. A unique set of quantum numbers (alway plus
one of the two possibilities for the spin) describes a state of the electron |
|
 |
Since these quantum numbers only appear in the wave vector k,
one often denotes a particular wave function by indexing it with k instead of nx,
y, z
because a given k vector denotes a particular solution or state
just as well as the set of the three quantum numbers. |
| |
| ynx, ny, nz(x,y,z) |
= |
yk(x,y,z) = yk(r)
|
|
|
|
 |
In other words, in a formal, more abstract sense we can regard the wave vector
as a kind of vector quantum number designating a special solution of the Schrödinger equation for the given problem. |
 |
Since in the present case the total energy E is identical to
the kinetic energy Ekin = ½mev 2 = ½p2/me,
we have |
| |
| E = |
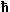 2 · k2 2 · k2
2me |
|
|
 |
We now have expressed the total energy as a function of
the wave vector. Any relation of this kind is called a dispersion
function. Spelt out we have |
| |
| E | = |
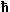 2 2
2me |
· |
æ
ç
è |
2 p
L |
ö
÷
ø | 2 |
· | æ
è
|
nx2 + ny2 + nz2
| ö
ø |
|
|
 |
This is the first important result: There are only discrete
energy levels for the electron in a box with constant potential that represents the crystal. |
|  |
This result (as you simply must believe at this point) will still
be true if we use the correct potentials, and if we consider many
electrons. The formula, however, i.e. the relation between energy and wave vectors may become much
more complicated. |
 |
The boundary conditions chosen and the length L of the box are somewhat arbitrary.
We will see, however, that they do not matter for the relevant quantities to be derived from this model. |
| | |
|
Density of States |
| | |
 |
Knowing the energy levels, we can count how many energy levels
are contained in an interval DE
at the energy E . This is best done in k-space or phase space. |
| |
| |
|
 |
For the free electron gas, in phase space a surface of constant energy is a sphere,
as schematically shown in the picture. |
|
|
 |
Any "state", i.e. solution of the Schroedinger equation with a specific k,
occupies the volume given by one of the little cubes in phase space, corresponding to the discrete states just discussed. |
| |
 |
The number of little cubes fitting inside the sphere at energy E thus is the
number of all
electronic states y up to E. |
| |
 |
Since every state (characterized by its set of quantum numbers nx, ny,
nz ) can accommodate 2 electrons (one with spin
up, one with spin down), the total number of electrons that can occupy states up to E
is twice the number of little cubes; let this number (that includes the spin degeneracy) be Ns
(E). |
| | |
|  |
Looking just at the energy, it is clear that at higher energies there are more states available.
Counting the number of little cubes just in an energy interval E, E + DE
corresponds to taking the difference of the numbers of cubes contained in a sphere with "radius" E + D E and E. |
|
 |
We thus obtain the density of states
D(E)
as |
| |
| D(E) | = | 1
V |
· | Ns(E + D
E) – Ns(E)
DE | = | 1
V |
· | dNs
dE | = |
| 1
L3 | · |
dNs
dE |
|
|
|
 |
Note that D(E) is a density both with respect to E and
to V = L3 (= volume of the crystal). |
 |
The final formula is |
| |
| D(E) = |
1
L3 |
· |
dNs
dE | = |
1
2p 2 |
æ
ç
è |
2me
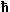 2 2 | ö
÷
ø |
3/2 | · | E
1/2 |
|
|
|
 |
The derivation of this formula and more
to densities of states (including generating some numbers) can be found in the link. |
 |
Some important points are: |
|
 |
- D(E) is proportional to E1/2.
- For different (but physically meaningful) boundary conditions we obtain the same D (see the exercise 2.1
below).
- The artificial length L disappears because we are only considering specific quantities, i.e. volume densities.
- D is kind of a twofold
density: It is first the density of energy states in an energy interval and second
the (trivial) density of that number in space .
|
|  |
If we fill the available states with the available electrons at a temperature of
0 K (since we consider the free electrons of a material this number will be about 1 [or a few]
per atom and thus is principally known) starting from E = 0, we find a special energy called Fermi
energy
EF
at the value where the last electron finds its place. |
| |
|
 |
In order to get (re)acquainted with the formalism, we do two simple exercises: |
| |
| Exercise
2.1-1 |
| Solution of the free electron gas problem with fixed boundary conditions |
|
|
| | |
|
Carrier Statistics |
| | |
 |
We have the number of energy states for a given energy interval and want to know
how many (charge) carriers
we will find in the same energy interval in thermal equilibrium . Since we want
to look at particles other than electrons too, but only at charged particles, we use the term "carrier" here.
|
 |
In other words, we want the distribution of carriers on the available energy levels
satisfying three conditions: |
|
 |
The Pauli
exclusion principle: There may be at most 2 carries per energy state
(one with spin "up", one with spin "down"), not more. |
|
 |
The equilibrium condition: Minimum of the appropriate
thermodynamic potential, here always the free Enthalpy
G (also called
Gibbs energy). |
|
 |
The conservation of particles (or charge)
condition; i.e.constant number of carriers regardless of the distribution. |
 |
The mathematical procedure involves a variation principle of G. The result is
the well-known Fermi
–Dirac distribution f(E,T): |
|
 |
f(E,T) = probability for occupation of (one!) state at E for the temperature
T |
| |
f(E, T) =
|
1
|
| exp |
æ
è |
E – EF
kT |
ö
ø |
+ 1 |
|
|
|
 |
If you are not very familiar with the distributions in general or the Fermi
distribution in particular, read up on it in the (German) link. |
 |
This is the "popular" version with the Fermi energy
EF as a parameter. In the "correct" version, we would have the chemical potential
m
instead of EF. |
|
 |
Since the Fermi energy is a quantity defined independently of the equilibrium considerations above, equating
EF with m is only correct at T = 0 K. Most textbooks
emphasize that small differences may occur at larger temperatures, but do not explain what those differences are. We, like
everybody else, will ignore these fine points and use the term "Fermi Energy"
without reservations. |
|
 |
In all experience, many students (and faculty) of physics or materials science have problems
with the concept of the "chemical potential". This is in part psychological
(we want to do semiconductor physics and not chemistry), but mostly just due to little acquaintance with the subject. The
link provides some explanations and examples which might help. |
 |
The Fermi-Dirac distribution has some general properties which are best explained in a graphic
representation. |
| |
|
|
 |
It contains a convenient definition of the Fermi energy: The energy where exactly half of the available
levels are occupied (or would be occupied if there would be any!) is the Fermi energy: |
| |
|
|
 |
The width of "soft zone" is » 4 kT
= 1 meV at 3 K, and 103 meV at 300K. |
|
 |
For E – EF >> kT the Boltzmann approximation can be used: |
|
|
| fB(E,T) » exp |
æ
è |
– |
E – EF
kT |
ö
ø |
|
|
|
 |
In this case the exclusion principle is not important because there are always plenty of free states around –
the electrons behave akin to classical particles. |
 |
This leads to the final formula for the incremental number or density
of electrons, dn, in the energy interval E, E + DE
(and, of course, in thermodynamic equilibrium). |
|
|
| In words: | Formula |
Density of electrons in the energy interval E, E + DE
=
density of states times probability for occupancy
times energy interval |
|
|
 |
This is an extremely important formula, which is easily generalized for almost everything.
The number (or density) of something is given by the density of available places times the probability of occupation. |
|
 |
This applies to the number of people found in a given church or stadium, the number of photons inside a "black box", the number of phonons in a crystal,
and so on. |
|
 |
The tricky part, of course, is to know the probabilities or the distribution
function in each case. However, if we do not consider church goers or soccer fans, but only physical particles (including
electrons and holes, but also "quasi-particles" like phonons,
excitons, ...), there are only two distribution functions (and the Boltzmann distribution
as an approximation): The Fermi-Dirac distribution for Fermions, and the Bose-Einstein distribution for Bosons. Mother nature
here made life real easy for physicists. |
 |
Since all available electrons must be somewhere on the energy scale, we always have a normalization
condition for the total electron density n: |
|
|
| n | = |
¥
ó
õ
0 | D(E) · f(E,T) · dE |
|
|
| | |
|
© H. Föll (Semiconductors - Script)