Density of States

Derivation of D(E ) for the three-dimensional free electron gas

	We start from the number of states inside a sphere with radius k in phase space.
		The volume V of the sphere is V = (4/3) · p · k3; the volume V k of one unit cell (containing two states: spin up and spin down) is
		Vk  =  æ ç è 2p L ö ÷ ø 3
		This gives the total number of states, Ns, to be
		Ns   =  2 · V  Vk  = 2 ·  4 · p · k3 · L3 3 · 8 ·p3  =  k3 · L3 3p2
		For reasons that will become clear very soon, we will keep track of the dimension of what we get. The wave vector k has a dimension of [k] = m–1; Ns thus is a dimensionless quantity - as it should be.
	The density of states D is primarily a density on the energy scale, and only secondarily a density in space. The definition was
		D  =  1  V · dNs dE  =  1  L3 · dNs dE
	We thus must express the wave vector in terms of energy which we can do using the appopriate dispersion relation. For the free electron gas model we have
		E  =   ( · k)2 2m k  =  ±  æ ç è 2 · E · m 2 ö ÷ ø 1/2
		Insertion in the formula for Ns yields
		Ns  =   L3 3p2  ·   æ ç è 2 E · m 2 ö ÷ ø 3/2   =  L3 3p 2 · (2m)3/2 3  ·  E 3/2
	Dividing by L3 and differentiating with respect to E gives the density of states D
		D  =   1 L3   ·  dNs dE   =   1  2p2  ·  æ ç è 2m 2 ö ÷ ø 3/2  ·  E 1/2
		The dimension now is somewhat odd, we have (with Plancks constant = h/2p = 6.5820 · 10–19 eV·s)
		[D]  =  kg3/2 · eV1/2 · eV–3 · s– 3  =  kg3/2 · eV– 5/2 · s– 3
		while we would need [D] = m–3 · eV–1 .

	If we want to calculate numbers, we have to find the proper conversion. The problem came from the dispersion relation which gave the dimension of the energy as
		[E] = eV2 · s2 · m–2 · kg–1 ; which tells us that eV · s2 · m–2 · kg–1 = 1 must hold.
		This is indeed the case, of course, because the basic unit of energy, the Joule, is defined as 1 J = 1 kg ·m2 · s–2 = 6.24 · 1018 eV.
		Substituting the kg in the dimension of D gives
		1 kg  =  6.24 · 1018 eV · m– 2 · s2       1 kg3/2  =  1.559 · 1028 eV3/2 · m– 3 · s3
	Insertion into the dimensions for D gives the right dimension and yields for masses given in kg, length in m and energies in eV:
		D  =   1.559 · 1028 æ ç è 2m ö ÷ ø 3/2  ·  E 1/2    [eV–1 · m–3 ] 2p 2 2                          =   7.90 · 1026  ·  æ ç è 2m ö ÷ ø 3/2 · E 1/2   [eV–1 · m–3]   2

Effective Density of States

	In all practical calculations, the effective density of state Neff is used instead of D(E). Neff is just a number, lets see how we can this from the free electron gas model.
		Lets just look at electrons in the conduction band; for holes everything is symmetrical as usual. We want to get an idea about the distribution of the electrons in the conduction band on the available energy states (given by D(E)).
	We have in fulll generality for ne = density of electrons in the conduction band
		ne  =  E* ó õ EC D(E') · f(E',T ) · dE'
		With f(E', EF, T) = Fermi-Dirac distribution, and the integration running from the bottom of the conduction band to the top of the band at E*, (or to infinity in practice). The dash at the symbol for the energy, E', just clarifies that the zero point of the energy scale is not yet the bottom of the conduction band.
		Of course we use the Boltzmann approximation for the tail end of the Fermi distribution and obtain
		ne  =  ¥ ó õ EC D(E') · exp æ è – E' – EF kT ö ø   · dE
	If we now take the bottom of the conduction band as the zero point of the energy scale for D(E) , we have E = E' – EC with EC = energy of the conduction band. Insertion in the formula above gives
		ne  =  exp æ è – EC – EF kT ö ø   ·   ¥ ó õ 0 D(E) · exp æ è – E kT ö ø   · dE
	Inserting the density of states from above with the abbreviation
		N0  =   1 2p 2 æ ç è 2m 2 ö ÷ ø 3/2
		gives a final formula for computing
		ne  =  exp æ è – EC – EF kT ö ø   · N0 ·   ¥ ó õ 0 E1/2 · exp æ è – E kT ö ø · dE
		The definite integral 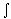[E1/2 · exp(–E/kT)]dE can be found in integral tables; its value is (1/2) · (p1/2) · (kT)3/2 .
	Insertion, switiching from to h, and some juggling of the terms gives the final result defining the effective density of states Neff
		ne  =  2· æ ç è 2p · m · kT ö ÷ ø 3/2  · exp æ è – EC – EF ö ø    =:  Neff · exp æ è – EC – EF ö ø h2 kT kT
	We now have the final result
		Neff  =  2 · æ ç è 2p · m · kT ö ÷ ø 3/2 h2
		And this is the formula we used in the backbone.
	What about numbers and the dimension? We have
		[Neff]  =  kg3/2 · eV3/2 · eV–3 · s–3  =  kg3/2 · eV–3/2 · s–3
		From before we have 1 kg3/2 = 1.559 · 1028 eV3/2 · m–3 · s3. Inserting this finally gives (for masses given in kg, length in m and energies in eV):
		Neff   =    4.59 · 1015 · T3/2 cm–3         =    2.384 · 1019 cm–3     (T = 300 K)     =    2.384 · 1025   m–3
		And those are very useful numbers – in particular, becasue they are quite close to the "real" (i.e. measured) values for Si.

With frame

2.1.1 Essentials of the Free Electron Gas

2.2.1 Intrinsic Properties in Equilibrium

Solution to 3.1.1

© H. Föll (Semiconductors - Script)