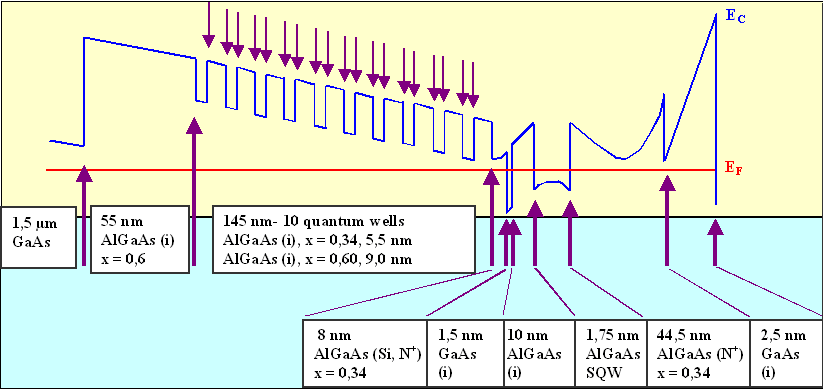
|
In this sub-chapter we will look at some major properties of heterojunctions.
First of all: How do we construct a band diagram? |
|
 |
Let's first look at the basic cases that we may encounter when considering heterojunctions.
Naturally, the bandgaps are always different, but only specifying Eg(1) and Eg(2)
[and of course the Fermi energy in (1)
and (2)] is not sufficient to describe the heterosystem before the contact
of the materials (1) and (2). |
|
 |
We also must specify the exact position on the
energy scale of one of the band edges. This then gives rise to three distinct
cases for heterojunctions as illustrated below together with the necessary definitions of the various energies needed. |
|
 |
You may want to consult a special
module (in German) dealing with some of the questions that may come up. |
| |
|
 |
Looking at the left hand case (Type I), we first discuss the various energies
encountered: |
|
 |
In contrast to "simple" band diagrams in Si, the vacuum energy level is now
included (and defines the zero point of the energy axis). We also have the energy of the band edges, EC
and EV, and from their difference the bandgap energy Eg. |
|
 |
By convention, the difference between the conduction band edge and the vacuum energy is defined
as a potential called "electron affinity
c"; q · c is thus the work needed
to move a charge from the (lower) conduction band edge to infinity.
|
|
 |
Note that this is not exactly the same as the electron
affinity in more chemical oriented lingo, where it is the energy gained by the reaction X + e– =
X– and thus only defined by atoms that form stable negatively charged ions. |
|
 |
The difference between the Fermi energy and the vacuum energy is given by charge times the
workfunction
Q
of the material, q · Q is thus the energy needed to move a fictitious
electron (because in semiconductors usually there is none at the Fermi energy) from the Fermi energy to infinity.
|
|
 |
Note that while c is a material
constant, Q
is not – it changes with the position of the Fermi energy. |
|
 |
We may also define the differences of the band edges between the two materials, DE
C and DEV, although they are implicitly given by the prime
material parameters c and E
g = EC – EV. |
 |
The three types of heterojunctions possible are: |
|
 |
Type I (straddling): The bandgap of one semiconductor is completely contained in the
bandgap of the other one; i.e. EC(2)
> EV(1) and EV(2) < EV(1). The discontinuities
of the bands are such that both types of carriers, electrons and holes, need energy (DEC
and DEV, resp.) to change from the material with the smaller band gap
to the one with the larger gap – the carriers from the other side loose this energy when they cross the junction.
Type I heterojunctions are quite common, the important GaAs/AlGaAs system belongs to this kind. |
|
 |
Type II (staggered): The bandgaps overlap, but one DEC
or V changes sign. The situation with respect to moving carriers from (1) to (2) or vice verse is
no longer symmetrical. One kind of carrier gains energy (in the example if electrons move from right to left), the other
one needs energy (the holes). The InP/InSb system provides an example. |
|
 |
Type III (broken-gap): The bandgaps do not overlap at all. The situation for carrier
transfer is like type II, just more pronounced. The system GaSb/InAs belongs to this type. |
| |
|
|
Construction of Band Diagrams |
| | |
 |
What happens if we join the two materials? Exactly
the same thing as for differently doped Si: |
|
 |
Carriers will flow across the junction, building space charges (and now possibly also interface
charges) until the Fermi energy is the same everywhere in the material. Far away from the junction, everything is unchanged. |
|
 |
However, there are pronounced differences to the case of a p–n junction in Si.
Let's imagine symmetrical junctions, i.e. the majority carrier density is identical in the p- and n-part.
For homojunctions , the number of electrons flowing into the p-type part is
then the same as the number of electrons flowing into the n-part. However, at least in the type I case, only
one kind of carrier will flow as is obvious and shown below. The space charge regions
to the left and right of the junction thus might not be symmetric. |
|
|
|
|
 |
Still, some kind of carrier transfer will happen and the electrostatic potential far away
from the junction will rise from a constant level on one side to a different, but constant level on the other side. The
difference will be equal to the difference in Fermi energy before the contact divided by the elementary charge. To the left
and the right of the junction the bands are bend accordingly, and so is the vacuum energy. |
 |
Let's see how far this recipe takes us with a simple GaAs–AlGaAs
type I junction: |
| |
|
|
 |
First, we align the Fermi energies. Then, we bend the bands – in a smaller region on
the more heavily doped side, but always identical for both band edges! After all, the vacuum potential at some position
x is fixed and so are the band edges relative to the vacuum potential. |
 |
This leaves us with something new: We
cannot join the bands of the two materials! If we adjust the band bending on both sides so that the conduction
bands match, the valence band won't match and vice verse. We must introduce a discontinuity
right at the interface at one of the bands – or at both. |
|
 |
The next picture shows how to do that for type I heterojunctions for both possible
doping cases. |
| |
|
|
 |
Some kind of cusp or notch must form in the conduction or valence band, depending on the details
of the system. Exactly what happens and what the cusps look like depends on many details, you must solve the Poisson equation
properly for a specific case. |
|
 |
Again, a discontinuity like this must happen, even at
"ideal" interfaces. We don't know exactly what it looks like, but we can now take this potential and plug it into
a one-dimensional Poisson equations and see what it means for the charge distribution. |
|
 |
Unavoidably, there must be a dipole layer right at the
interface (look at this basic module if you have problems figuring that
out). The distance between the charges of this dipole layer is so small, however (atomic size) that it does not influence
the carrier movement (there is an acceleration/de-acceleration process with equal magnitudes at a very small scale in classical
terms or effortless tunneling in quantum-mechanical terms). |
|
 |
This dipole layer with its sharp wiggle in the charge distribution is therefore usually not
included in drawings of the heterojunction. |
 |
In reality, the matching of two lattice types with different atoms on both sides
may well introduce some interface states in the bandgap, as discussed
for the free Si surface. |
|
 |
Depending on the Fermi energy (which is of course influenced by the interface states, too),
these interface states may be charged and introduce some band bending of their own. |
 |
To make things even more complicated (for pessimists),
or to add more possibilities for engineering with heterojunction (for optimists), we
now can produce junctions with specific properties between materials of the same doping
type – even for identical carrier densities. |
|
 |
This type of heterojunction is sometimes called an isotype
junction , the p–n type a diode-type junction. Some
people use abbreviations, with upper case letters indicating the doping type of the material with the wider bandgap and
lower case letters the other one. We then have Pn, pN, Np, and nP junctions of the diode type, and Nn, nN, Pp, and pP junctions of the isotype.
If we look ahead, we can now easily denote multi-junctions like PnP, and so on. |
|
 |
Also isotype junctions have band discontinuities at the interface, and also here the cusp
is where the Fermi energy is; the next picture shows examples. |
|
|
|
|
 |
You may already wonder what properties to expect from this kind of junction and what it is
good for; we will discuss that later. |
 |
We now have a degree of freedom for all heterojunctions, which did not occur for
homojunctions: How do we distribute the discontinuity? |
|
 |
In the left hand diagrams above, e.g., we could decrease DEC
and increase DEV by an identical amount, making the cusp more pronounced;
or we do it the other way around. How can we find the real case? |
|
 |
The answer is: Nobody knows how to do that in some kind of comprehensive theory. The simplest
model (called the Anderson model) assumes that DEC
is equal to the difference in the electron affinities c: |
| |
|
|
 |
But that is only a rough estimate that may be quite wrong – not to mention that bulk electron affinities cannot be calculated with any precision, and measurements always
obtain the (systematically different) surface electron affinities. |
 |
There is, however, one feature of the discontinuities that makes life somewhat
easier: Whatever its value, it is determined by the interaction of the atoms at the interface and interatomic forces are
responsible for its value. |
|
 |
This simply means that its value does not change much if we change properties of the materials
on a scale much larger than the atomic scale. In other words: |
|
 |
The band bending necessary for adjusting the potentials
on both sides of the junction, so that the Fermi energy is identical, may be seen as independent of the value of the discontinuities.
If we construct a band diagram, we simply always keep the same value for the discontinuities (as determined from using the
vacuum level as reference for the separate bulk materials), no matter what else we do with the bands. |
| | |
|
Properties of Heterojunctions |
| | |
 |
How do we measure the values of the discontinuities? The answer is: Make the heterojunction
and measure the junction properties. |
|
 |
In order to do that, we need to know how the discontinuities influence measurable quantities.
How, for example, does the precise nature of the discontinuities influence the current–voltage characteristic of a
heterojunction? Or, if there is some radiative recombination, the quantum- or current
efficiencies? |
|
 |
We are now entering deep water. Or
are we? After all, the equations for I–V characteristics of a junction (without the space charge
layer part) in the simple or more complex
form did not contain anything about the shape of the band bending – only the potential difference and bulk properties
of materials to the left and right of the junction. |
|
 |
This tells us that the basic
diode characteristics (assuming that nothing happens in the space charge region) must still be valid in its general
form, but with one big difference that transfers into a decisive property of heterojunctions:
|
|
 |
The hole and electron part of the total current now are different
even for a perfectly symmetric junction! |
 |
This is most easily seen if we look at the relation between the two partial currents
je and jh, called the injection ratio k = je / jh
. Taking the expressions from the simple diode equation given
before, we obtain |
|
|
| k | = |
je
jh |
= |
e · nep · De / Le
e · nhn · Dh / Lh |
|
|
|
 |
Rewriting this in terms of the carrier mobilities and the doping densities (assuming fully
ionized dopants) with the relations given before, we obtain |
| |
| k = |
[me · ni
2 / (Le · NA)] p-side
[mh · ni2
/ (Lh · ND)] n-side |
|
|
|
 |
For homojunctions, the intrinsic carrier density ni
is the same on both sides, but not for heterojunctions! For the intrinsic carrier
densities of any semiconductor we have the basic equations: |
| |
| nei | = |
Neeff · exp |
æ
ç
è |
– | EC – EFi
kT | ö
÷
ø
| | |
| | | |
| | |
| nhi | = |
Nheff · exp |
æ
ç
è |
– | EFi – EV
kT | ö
÷
ø
| = | nei |
|
|
|
 |
With EFi = Fermi energy for the intrinsic case. |
 |
Only for the case that N
e eff = N
heff would the Fermi energy be in the middle of the band gap; and while we always used
that approximation for Si, we must be more careful with compound semiconductors. |
|
 |
But independent of the exact position of the Fermi energy, for total equilibrium we always
have |
| |
| ni 2 | = |
ne i · nhi = N
eeff · Nheff · exp |
æ
ç
è |
– | EC – EV
kT | ö
÷
ø
|
|
|
|
 |
Inserting this relation into the equation for the injection ratio k
from above, introducing the difference of the band gaps of material 1 and material 2 as DEg
= Eg(1) – Eg(2), and substituting "1" and "2"
for "n-side" and "p-side" (because this relation is valid for any
heterojunction of the diode type), we obtain for k: |
| |
| k = |
[ me · Neff
e · Neffh / (Le · NA )]1
[ mh · Neffe
· Neffh / (Lh · ND)]2 |
· exp |
æ
ç
è |
– |
DEg
kT |
ö
÷
ø |
|
|
 |
This is a very important equation for optoelectronics. Let's
see why: |
|
 |
If DEg is sufficiently large – and
since it is in an exponential term, it does not have to be very large – it will
always overwhelm the possible asymmetries in the pre-exponential term, e.g. because of different doping levels, or effective
density of states between the two materials, and this means k = je
/ jh is very different from 1. Getting all signs right, we have the following situation: |
| |
| Junction type | DEg |
exp [–D Eg/(kT)] |
k | | Pn | >0 | small | small |
| pN | <0 | large | large |
|
|
 |
In other words: In heterojunctions of the diode
type, injection of the majority carriers from the material with the larger band gap (almost) always far surpasses the reverse
process. |
|
 |
To give a relevant example: For a GaAs/Ga0.7Al0.3 As junction
with DEg = 0.3 eV and for doping densities of 1018 cm–3
or 2 · 1017 cm–3, respectively, we have k
» 106. |
 |
Why is a large value of k
so important? |
|
 |
Because if we sandwich a small gap semiconductor between
two large gap semiconductors, we should be able to inject a lot of electrons from one
side and a lot of holes from the other side – with no means of escape. The injected carriers must
recombine in the small gap part, which thus is our recombination zone – we have a large
current efficiency hcu. |
|
 |
If you think about that a minute and try to come up with some structure,
you will realize that there is a problem: You cannot have injection via two
p–n junctions – one junction must be an isotype junction.
But luckily, isotype junctions have similar properties: it is easy to inject majority carriers from the wide band gap side
and not so easy from the other side. |
|
| |
© H. Föll (Semiconductors - Script)