5.2.2 Absorption and Emission of Light

Absorption of Light in Semiconductors

The optical efficiency h_opt is easy to understand by looking a the mechanisms that prevent photons from leaving the device. We have two basic mechanisms:

1. The photon is absorbed before arriving at a (possibly internal) surface of the device.

2. The photon makes it to the (internal) surface of the device, but is reflected back into the interior and then absorbed.

We thus have to worry about absorption of light in semiconductors in general and about reflections at surfaces.

The first topic is a science in itself. Here we only note a few of the major points:

In direct analogy to the various modes of radiative recombination, we have the reverse process, too: A photon creates an electron hole pair occupying some levels (including, e.g. exciton levels).

All the conservation laws must be obeyed; phonons or other third particles (in the general sense; some defects might come in handy here) may have to assist the process.

The dominating absorption process usually is the direct band–band process, i.e., straight up in a (reduced) band diagram from an (occupied) position in the valence band to an (unoccupied) position in the conduction band. (For indirect semiconductors this requires a larger energy than the band gap!)

The band–band absorption process is also called the fundamental absorption process, it is described phenomenologically by Beer's law:

The intensity I of the light at a depth z in the semiconductor, I ( z ), is given by

I ( z )	= I₀ · exp (– a · z)

With I₀ = intensity at z = 0 and a = absorption coefficient of the material.

It is clear that a = a(hn) is a strong function of the energy hn of the photons:

For hn < E_g(direct), no electron–hole pairs can be created, the material is transparent and a is small.

For hn ³ E_g(direct), absorption should be strong.

All mechanisms other than the fundamental absorption may add complications (e.g. "sub band gap absorption" through excitons), but usually are not very pronounced.

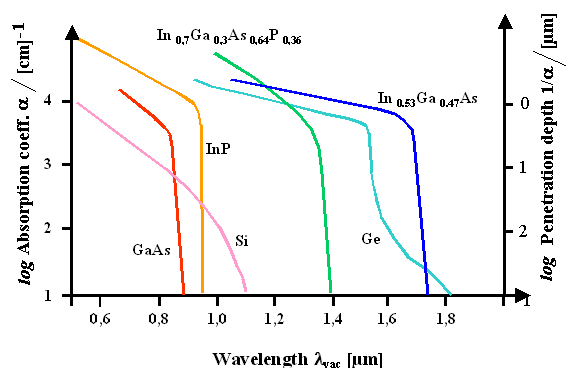
The absorption coefficients of major semiconductors indeed follow this predictions as can be seen in the following diagram:

Absorption cOefficient Of variOus semicOnductors

As expected, the absorption coefficient changes by 4 ... 5 orders of magnitude around the band edge energy, and in direct semiconductors this change is "harder" than in indirect semiconductors.

Note that the absorption edge of Ge shows the features of both an indirect and a direct transition, the latter one occurring only slightly higher in energy than the former. This is fully consistent with the band structure of germanium (cf., e.g., here).

There are many more points to the absorption of light in semiconductors, but we will not pursue the issue further at this point.

The optical efficiency h_opt

If we now look at an LED, we notice that light with wavelengths corresponding to the absorption edge thus will be absorbed within a few µm of the material – and that automatically applies to the light emitted by radiative recombination .

If we look at a naive cross section of a light emitting diode (on the left), we see that only light from the edges of the p–n junction has a chance to make it to the surface of the device. Obviously, this is not a good solution for a large optical efficiency.

If we make a junction more like in an integrated Si circuit (above right), the situation is somewhat improved, but it might be difficult to drive high currents in the central region of the device, far away from the contacts.

We might be better off in choosing an n-type material with a larger bandgap than the p-type material and see to it that light is generated in the p-type material. Its photon energy then would be too small for absorption in the large bandgap material and it could escape without absorption. In other words: We utilize a heterojunction (see below for details).

This sequence demonstrates several important points about the realization of LEDs:

1. A large optical efficiency is not easy to achieve. Generally, much of the light produced will never leave the device.

2. The typical structures from Si integrated circuit technology may or may not be useful for optoelectronic applications. In general, we have to develop new approaches.

3. We always should try to produce the light close to the (possibly internal) surface of the active material. In other words, we need a defined recombination zone that is not deep in the bulk of the active material.

4. Heterostructures – meaning the combination of different semiconductors – come up quickly in optoelectronics (while virtually unknown in Si technology – except for high-efficiency solar cells).

Next, let's assume that the photons make it to the surface of the device. The question now is if they are reflected back into the interior or if they can escape to the outside world.

This is a question that can be answered by basic optics. The relevant quantities are shown in the next picture.

For the light beams coming from the interior of the semiconductor to the interface (air in the picture; more generally a medium with a refractive index n₂), Snellius' law is valid:

n₁ · sin Q₁	=	n₂ · sin Q₂

With n₁ = index of refraction of the semiconductor, n₂ = index of refraction of the outside (= 1 if it is air).

Since relevant semiconductors have rather large refractive indexes (simply given by the square root of the dielectric constant), refraction is quite severe.

As soon as Q₂ reaches 90°, light will be reflected back into the semiconductor; this happen for all angles Q₁ larger than Q_crit, the critical angle for total reflection, which is obviously given by

Q_crit	=	arcsin	n₂ n₁

For typical refractive indices of 3.5 (or dielectric constants e_r = 12.25), we have Q_crit = 17°. This is a severe limitation of h_opt: Assuming that radiation is produced isotropically, a cone of 17° contains only about 2% of the radiation!

But the situation is even worse because photons within the critical angle may still become reflected – the probability is < 1, but not zero.

For the transmissivity T, the fraction of light that does not get reflected, the following relation (a variant of the general Fresnel laws of optics) holds:

T = 1 –	æ ç è	n₁ · cosQ ₁ – n₂ · cosQ₂ n₁ · cosQ₁ + n₂ · cosQ₂	ö ÷ ø	²	= 1 – R

With R = reflectivity = {intensity of reflected beam} / {intensity of incoming beam}.

This can be simplified to an expression for the total fraction of light leaving the semiconductor:

T_total	»	4 · n₁ · n₂ (n₁ + n₂)²

For n₁ » 3.5 and n₂ = 1 (air) we have T_total = 0.69, so only about 2/3 of the radiation contained within the critical angle leaves the semiconductor.

The total optical efficiency of LEDs with isotropic generation of radiation thus is in the 1% region – something we must worry about!

The simplest solution is to "grade " the refractive index, i.e. to lower it in steps. This is most easily achieved with a "drop" of epoxy or some other polymer. How this method of index grading works becomes clear from the drawing:

Two light rays at the edge of some aperture have been traced; the relevant angles are shown as pink triangles for the red light beam. The critical angle for total reflection at both interfaces is now considerably larger. Note that the angle in the lower index medium is always larger and that this leads to a certain, not necessarily isotropic radiation characteristics of the system.

The polymer layer, in other words, acts as an optical system – and by giving it specific shapes we can influence the radiation characteristics to some extent.

In total, we see that getting the light out of the device (and having it more or less focussed or otherwise influenced in its directional characteristics), is a major part of optoelectronic technology.

In fact, a totally new field of research with some bearing to these problems has recently be opened by the (first theoretical, and then experimental) "discovery" of so-called photonic crystals – activate the link for some details.