8. Leitfähigkeit und Bändermodell

8.1 Leitfähigkeit, Ladungsträgerdichte und Beweglichkeit

8.1.1 Ein neuer Blick aufs Ohmsche Gesetz

Das Ohmsche Gesetz

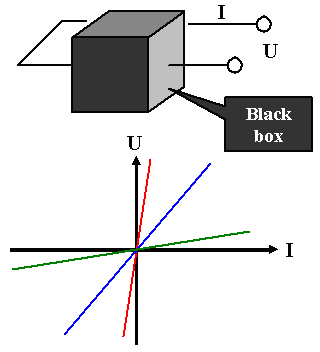
	Das Ohmsche Gesetz sagt bezüglich einer "Black Box", aus der zwei Drähte hängen, angeschlossen an eine Spannung U:
		R  =  U I
		In anderen Worten: der fließende Strom I ist proportional zur angelegten Spannung U. Der Widerstand R ist die Proportionalitätskonstante und beschreibt elektrisch gesehen vollständig, was auch immer in der Black Box im Detail abläuft.
	Das ist natürlich Kindergartenniveau. In der elektrischen Materialwissenschaft drehen wir das Ganze um: Sage mir, was für ein Material / Materialkombination in der Black Box drin ist, und ich sage dir:
		Ob das "Ohmsche Gesetz" überhaupt gilt. Wie groß – genau in Ohm – dann der Widerstand R sein wird, inklusive seiner T-Abhängigkeit usw. Was ansonsten passieren wird, wenn man eine Spannung anlegt.
	Wir nähern uns diesem sehr anspruchsvollem Programm in 3 Schritten:
		1. Wir schreiben das "Ohmsche Gesetz" um auf spezifische Größen.
		2. Wir rechnen mal aus, wie das zu den freien Elektronen in Metallen paßt, und erarbeiten uns dabei die Grundformel für alle Leitfähigkeiten.
		3. Wir realisieren, daß eine klassischen Betrachtung früher oder später direkt in den Abgrund führt, und retten das Ganze mit Quantentheorie und der uns bereits bekannten Fermiverteilung. Das bringt uns dann zwanglos auf Halbleiter.

	1. Schritt: Spezifische Größen
	Wie schon früher ausführlich begründet, sind Strom I und Spannung U aus Materialsicht inhaltslose Größen. Wir nehmen stattdessen Stromdichte j und Feldstärke E. Damit wird man nicht nur frei von Größe und Gestalt des Materials, sondern bekommt sogar sehr viel mächtigere Vektor beziehungen.
		Damit lautet das Ohmsche Gesetz:
		j  =  s  · E
		Daß die Gleichung stimmt, leiten wir uns schnell selbst her:
		Fragebogen Einfache Fragen zu 8.1
	Für einen Quader der Länge l, der Querschnittsfläche F und dem ohmschen Widerstand R gilt dabei für die spezifische Leitfähigkeit s = 1/r; mit r = spezifischer Widerstand
		s  =  1 r  =  l F · R
		Wir werden selbstredend den spez. Widerstand r nie mit der Ladungsdichte r oder allgemeinen Dichten von irgendetwas, gerne auch r genannt, verwechseln.
	Die (spezifische, aber das lassen wir in Zukunft weg) Leitfähigkeit hat die Dimension [s] = W–1 cm–1; der spez. Widerstand damit [r] = Wcm. Eigentlich sollte man [s ] = W–1m–1 nehmen, das ist aber eher ungebräuchlich. Hier muß man aber aufpassen!
		Ein paar Zahlen dazu, die man wissen sollte:
		r (Metall)  »  1 µ Wcm       r (Halbleiter)  »  1 W cm       r (Isolator)   »  1 GW cm

	2. Schritt: Die Grundformel für die Leitfähigkeit
	Bechränken wir uns erstmal auf Metalle und halten fest:
		Der elektrische Strom wird von freien Elektronen getragen. Sie "fließen" unter dem Einfluss eines elektrischen Feldes und transportieren dadurch Ladung.
	Definieren wir mal die durch die gedache Querschnittsfläche des Leiters im Bild unten fließenden Ladungen ganz allgemein:
		1. Der extern fließende elektrische Strom ist die Nettozahl der Ladungen die pro Sekunde durch die Querschnittsfläche fließen. Ausgedrückt in Stromdichten haben wir
		jnetto  =  jrot – jgrün
	Wieso ist der extern fließende Strom eine Differenz von Partialströmen ? Weil schon ohne angelegtes elektrisches Feld gewaltige "Ströme" durch unsere Bezugsebene fließen!
		Die Elektronen sitzen ja nicht still, sondern rennen im Kristall herum. Deswegen redet man auch gerne vom "Elektronengas" im Metall. In anderen Worten: Die freien Elektronen im Metallkristall verhalten sich so wie die Luftmoleküle im Raum. Sie haben (thermische) Energie und rennen wild durch die Gegend. So haben wir das schon mal gezeichnet.
		Wir wissen sogar, mit welchen mittleren Geschwindigkeiten sie das als klassische Teilchen (die sie nicht sind) tun würden. Wir rechnen das trotzdem aber schnell nochmals aus:
		Die Elektronen rennen also auch ohne elektrisches Feld mit ziemlich hoher Geschwindigkeit wild durcheinander. Sie stoßen dabei mit allem möglichen zusammen und ändern nach einer durchschnittlichen Stoßzeit t ihre Geschwindigkeit nach Betrag und Richtung – aber so, daß sich die Mittelwerte nicht ändern, denn es gilt Energie- und Impulserhaltung.
		Zwangsweise werden eine ganze Menge pro Sekunde auch von links nach rechts durch die Bezugsebene laufen, und ebenso zwangsweise werden genauso viele von rechts nach links laufen, falls auf beiden Seiten der Bezugsebene exakt dieselben Verhältnisse vorliegen.
	Genauso ist es. Ohne zusätzliches Feld sind die beiden Partialströme entgegegesetzt gleich groß – und individuell gigantisch viel größer als alles, was wir als "echten" Strom jemals herausbekommen können.
		Wenn wir jetzt ein Feld in z. B. –x Richtung (von rechts nach links) einschalten, werden alle Elektronen etwas gegen die Feldrichtung beschleunigt (nach rechts) und bekommen zu ihrer jeweiligen thermischen Geschwindigkeit noch ein Dvx überlagert.
		Nur dieses D vx sorgt jetzt für einen Nettostrom, denn es macht den Partialstrom von links nach rechts jetzt etwas größer als den rückfließenden Strom von rechts nach links.
		Wir nennen Dvx ab jetzt die Driftgeschwindigkeit vD der Elektronen; nur auf sie kommt es an. Die Driftgeschwindigkeit ist im Vergleich zur mittleren thermischen Geschwndigkeit sehr, sehr klein.
	Da die Driftgeschwindigkeit aber den Nettoeffekt direkt beschreibt, können wir sie nehmen, um jetzt auszurechnen, wie groß die Stromdichte bei einer gegebenen Zahl von Elektronen und ihrer Driftgeschwindigkeit ist.

		Wir haben: Stromdichte j = Zahl N der Elektronen mit der Ladung q = –e, die während der Zeit t durch die Querschnittsfläche F fließen, oder
		j   =  –e · N F · t
	Die Zahl N ist blöd, wir nehmen lieber die Dichte n = N/V .
		Dazu müssen wir das passende Volumen V = F · l so definieren, daß es gerade die richtig Zahl N an Ladungsträgern enthält. Das heißt, die Länge l muß so gewählt werden, daß alle Elektronen, die maximal l von der Bezugsebene weg waren, während der Zeit t noch durchfließen können.
		Das ist nun leicht. Wir müssen nur ansetzen:
		l  =  vD · t
		Fertig: Einsetzen (und, zwecks größerer Allgemeinheit, Ersetzen von –e für Elektronen durch q = irgendeine Ladung) ergibt:
		j  =  q · N F · t  =  q · n · V F · t  =  q · n · F · l F · t  =  q · n · F · vD · t F · t
	Das ist in exzessivem Detail gezeigt, denn es ist wichtig! Was rauskommt, ist:
		j  =  q · n · v D
	Das ist eine sehr allgemeine, sehr einfache und sehr wichtige Gleichung. Sie koppelt eine elektrische Stromdichte mit einem aus welchen Gründen auch immer mechanisch fließenden Teilchenstrom.
		Alles, was wir jetzt noch tun müssen, ist, diese Gleichung mit dem Ohmschen Gesetz von oben zu vergleichen. Wir erhalten

		j  =  q · n · vD  =  s · E
	Als Konsequenz ergibt sich für die Leitfähigkeit s
		s  =  q · n · vD E  =  constant
	Falls das Ohmsche Gesetz gilt, ist s eine Konstante, und das bedeutet dann notwendigerweise, daß
		vD E  =  constant
		Das ist eine weitere sehr einfache, aber weitreichende Gleichung. Sie sagt etwas aus über Ursache (elektrisches Feld) und Wirkung (Driftgeschwindigkeit); insbesondere sagt sie, daß trotz konstanter Kraft (F = q · E ) auf die Teilchen, und damit konstanter Beschleunigung (a = F/m), die im Mittel erreichte Geschwindigkeit (= vD ) konstant sein muß. Sonst gibt es kein Ohmsches Gesetz!
		Sowas gibt es klassisch eigentlich nur, wenn Reibung vorliegt. Wir schauen uns das auch gleich noch genauer an.
	Die Bedingung vD/E = constant muß für alle Materialien, die ohmsches Verhalten zeigen, erfüllt sein. Das sind eine ganze Menge, deswegen geben wir dieser Größe einen eigenen Namen:
		vD E  =   µ   = Beweglichkeit  =  wichtige Materialkonstante
		Die Beweglichkeit µ der Ladungsträger hat die Einheit [µ] = (m/s)/(V/m) = m2/(V · s).
	Die Beweglichkeit ist ein sehr wichtiger Materialparameter! Die moderne Mikroelektronik, Optoelektronik, Solarik usw. dreht sich immer auch um die Beweglichkeit; oft ist es der überragende Materialparameter für moderne Anwendungen!
	Mit der Beweglichkeit können wir jetzt die allgemeinste Gleichung oder Grundgleichung für die Leitfähigkeit angeben:
		s  =  q · n · µ
	In Worten: Die spez. Leitfähigkeit eines beliebigen Materials ist einfach das Produkt aus der Dichte n der beweglichen Ladungsträger, ihrer Ladung q, und ihrer Beweglichkeit µ.
		Sollte in einem Material überall und zu jeder Zeit in Bezug auf das elektrische Feld gelten: n = const. und µ = const. – dann, und nur dann, gilt auch das Ohmsche Gesetz in der Form U = RI. Sonst wird's komplizierter.
		Insbesondere setzt µ = const. voraus, daß die Driftgeschwindigkeit linear mit der Feldstärke ansteigt. Das ist für kleine Felder der Fall; für große steigt sie nicht weiter an, sondern geht in Sättigung (wobei es vom jeweiligen Material abhängt, was "groß" in diesem Zusammenhang bedeutet).
	Um die Frage 2 von oben jetzt abzuhaken, müssen wir nur noch (haha) die Ladungsträgerdichten und die Beweglichkeit berechnen. Und das nur aus der Kenntnis der Kristallstruktur und der Defekte in dem Kristall.
		Das ist nicht so ganz einfach – aber es geht! Zu bedenken ist, daß s über einen extrem großen Bereich variiert – und das muß man erst mal in der Theorie nachvollziehen können!
	Um mit den neuen Begriffen aber erstmal etwas vertraut zu werden, machen wir eine Übungsaufgabe.
		Übung 8.1-1 Bestimme Zahlen für µ und vD	Fragebogen Schnelle Fragen zu 8.1.1

© H. Föll (MaWi für ET&IT - Script)