8.1.2 Mittlere freie Weglänge, Stoßzeit und Beweglichkeit

Elektronen und Stöße

	Wir wollen's kurz machen und schauen uns gleich mal das erste Bild an.
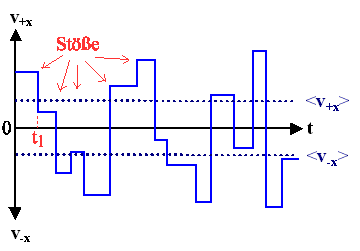
					Von links kommt ein (freies) Elektron in irgendeinem Metall geflogen, es hat irgendeine konstante Geschwindigkeit vx in +x-Richtung.
					Zur Zeit t1 ändert es abrupt seine Geschwindigkeit, es fliegt zwar weiterhin in +x Richtung, aber langsamer.
					Im Laufe der Zeit wiederholt sich das so im Mittel alle t Sekunden; manchmal läuft es jetzt auch rückwärts (–x-Richtung).
					Das ist schlicht das eindimensionale Bild eines statistisch herumirrenden Elektrons, also eines "random walk" Elektrons mit einer mittleren vektoriellen Geschwindigkeit <v> = 0, aber durchaus beträchtlicher mittlerer skalarer Geschwindigkeit |v| ¹ 0 – so im km/s-Bereich.
	Was passiert bei t1 und dann immer wieder nach rund und roh t Sekunden? Einfach: Das Elektron stößt mit "etwas" zusammen und fliegt danach mit geändertem Impuls und Energie weiter.
			Die Frage ist natürlich: Wer oder was kommt als Stoßpartner für Elektronen in Frage? Schau'n mer mal: Die Atome des Kristalls? Erstmal nein, denn sie haben die freien Elektronen abgegeben und sind nicht mehr an ihnen interessiert. (Eine tiefere Begründung dafür wird es im folgenden Unterkapitel geben.) Die anderen Elektronen? Erstmal nein, denn die Elektronen gehen sich gegenseitig aus dem Weg. Ein bißchen was geht zwar immer, aber Elektron-Elektron-Stöße sind nicht so wichtig. Defekte im Kristall, d. h. falsche Atome, Versetzungen, Korngrenzen usw.? Ja! Defekte sind in der Tat effiziente Stoßpartner! Die Temperatur? Ja – bloß: Wie stößt man sich mit der Temperatur? Nun ja – T ist ein Maß für die innere Energie, und die sitzt in den Schwingungen der Atome. Mit Atomen, die nicht still auf ihrem Gitterplatz sitzen, sondern durch ihre Bewegung die Symmetrie des Gitters stören, kann sich ein Elektron stoßen.
			In der Tat: Die thermischen Vibrationen der Atome (die man in "gequantelter" Form gerne auch Phononen nennt), streuen "per Stoß" die im Kristall herumflitzenden Elektronen. Das wird offenbar um so heftiger, je heißer der Kristall ist.
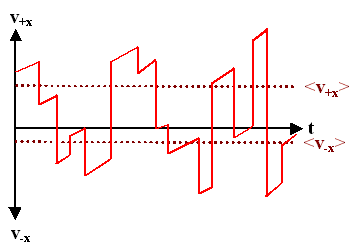
	OK – das obige Bild ist jetzt klar. Für den nächsten Schritt lassen wir erst mal alles, wie es ist, schalten aber jetzt noch ein elektrisches Feld ein, das die Elektronen nach rechts beschleunigt. Was wir dann erhalten werden, sieht so aus:
					Solange das Elektron friedlich vor sich hin fliegt, wird es jetzt beschleunigt, d. h. seine Geschwindigkeit in +x -Richtung steigt linear. Beim Stoß verliert es völlig "das Gedächtnis", und alles fängt wieder von vorne an.
					Die Durchschnittsgeschwindigkeit in +x -Richtung wird jetzt etwas größer sein als in –x-Richtung; wir haben <v> ¹ 0 = vDrift.
					Allerdings sind das in der Realität so kleine Effekte, daß sie auf einer maßstabsgetreuen Zeichnung gar nicht auffallen würden.
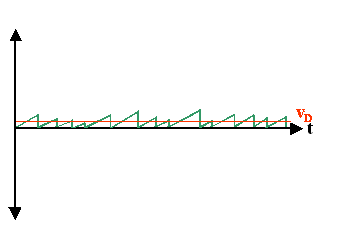
	Wir können die Zeichnung jetzt radikal vereinfachen, indem wir alles, was sich zu null mittelt, von vornherein weglassen. Das sieht dann so aus:
					Was bleibt, ist ein gewisser Geschwindigkeitszuwachs zwischen den Stößen mit dem vektoriellen Mittelwert vDrift oder vD = Driftgeschwindigkeit.
					Außerdem können wir, wie oben schon angedeutet, eine mittlere Stoßzeit t definieren, halt die mittlere Zeit zwischen zwei Stößen. (Genau genommen ist es die halbe Zeit zwischen den Stößen; mehr dazu weiter unten.)
					Damit verbunden ist dann automatisch noch eine mittlere freie Weglänge l = v · t; mit v = Gesamtgeschwindigkeit (skalarer Mittelwert) des Elektrons.
	Was hat das nun alles mit der Leitfähigkeit und der Beweglichkeit zu tun?

	Beweglichkeit und Stöße
	Wir schreiben einfach mal das Newtonsche Grundgesetz für ein friedlich seines Weges ziehenden Elektron hin:
		m · dv dt   =  m · Dv Dt   =  m ·  vD t    =  F  =  q · E Þ   vD   =   q · E · t m
		Das dv/dt haben wir einfach durch den mittleren Zugewinn an Geschwindigkeit = vD in der Zeitdifferenz t ausgedrückt (und das klappt nur, wenn t die mittlere halbe Zeit zwischen den Stößen ist). Das darf man, solange alles linear ist. Wir erhalten damit die angegebene Gleichung für die Driftgeschwindigkeit vD.
		Damit folgt unmittelbar:
		µ   =   vD E   =   q · t m
		Die Beweglichkeit µ ist also letztlich nichts anderes als die Stoßzeit t in Verkleidung. Da Stoßzeit und mittlere freie Weglänge l linear gekoppelt sind, können wir auch sagen, daß die Beweglichkeit direkt mit l skaliert.
	Das ist eine ganz schlechte Nachricht für ET&IT-Ingenieure!
		Bei Raumtemperatur gibt es selbst in einem perfekten Kristall noch die unvermeidbaren Stöße mit den "Phononen", den thermischen Gitterschwingungen. Damit kann die Beweglichkeit auch im perfekten Kristall (bei RT) nie beliebig groß werden. Die Ladungsträgerdichte ist schlicht durch das Material gegeben – rund und roh ein bis maximal einige wenige Elektronen pro (Metall-)Atom – und damit liegt s = q · n · µ für den perfekten Kristall erst mal fest.
		Ist dieser Wert für ein gegebenes Material nicht gut genug, versagt der übliche Trick der Materialwissenschaftler: Wirf noch dieses oder jenes rein (mach Legierungen). Denn was immer man tut, man erzeugt Defekte, und jeder Defekt wird die Beweglichkeit bestenfalls gar nicht ändern, aber im Zweifel immer nur kleiner machen! Damit geht die Leitfähigkeit relativ zum perfekten Kristall immer nur runter!
		Leider sind auch die besten Leitfähigkeiten von Materialien wie Cu oder Ag nicht gut genug für moderne ET&IT-Produkte wie Mikrochips oder Solarzellen. Um trotzdem erfolgreich zu sein, braucht's jede Menge Gehirnschmalz (und sehr viel Geld).
	Im Grunde können wir jetzt anfangen zu rechnen. Das tun wir auch mal – in einer Übungsaufgabe:
		Übungsaufgabe Aufgabe 8.1-2
		Es lohnt sich, die Aufgaben mal anzuschauen – insbesondere den Teil über die mittlere freie Weglänge, denn:
		Es kommt Unsinn raus!

	Der Zusammenbruch der klassischen Sichtweise
	Was haben wir falsch gemacht?
		Wir haben klassisch gerechnet und die mittlere Geschwindigkeit eines Elektrons aus dem Gleichverteilungssatz bestimmt. Das darf man nicht!
		Für ein typisches Metall mit einem spez. Widerstand im Bereich von mWcm erhält man klassisch mittlere freie Weglängen im Nanometer-Bereich – und das ist Unsinn!
	Die möglichen Stoßpartner für Elektronen (z. B. Defekte) müssen bei sehr guter Leitfähigkeit sehr viel weiter auseinanderliegen als wenige Gitterkonstanten; wir liegen mindestens um einen Faktor 100 daneben!
		Wir haben aber klassisch gesehen nichts falsch gemacht. Alle Formeln stimmen – auch dann noch, wenn mehrere Nobelpreisträger das beliebig verkomplizieren. Klassisch ist hier nichts zu retten.
		Quantenmechanisch schon! Wir haben nur zu berücksichtigen, daß Elektronen Fermionen sind und dem Pauli-Prinzip unterliegen! In anderen Worten:
		Der Gleichverteilungssatz gilt nicht für Fermionen!
		Das haben wir übrigens schon gelernt – unter diesem Link mal nachsehen.
	Im nächsten Modul schauen wir uns die Lage dann aber "richtig" an.
		Fragebogen Schnelle Fragen zu 8.1.2

© H. Föll (MaWi für ET&IT - Script)