|
Dichteste Kugelpackungen sind uns
schon mehrfach begegnet. Sie sollten automatisch
auftreten, falls Atome der gleichen Sorte ungerichtete Bindungen eingehen. Wir haben auch schon gesehen, dass
eine dichteste Kugelpackung in zwei Varianten vorkommt: |
|
 |
Hier schauen wir uns diese beiden Varianten schnell noch etwas genauer an. |
 |
Wir verwenden eine neue Methode, um einen dicht gepackten Kristall zu bilden:
Wir arrangieren seine Bausteine (die Basis) erst mal in einer
Ebene (hier also schlicht Atome derselben Sorte), und wir packen sie gleich noch so dicht als möglich. |
|
 |
Das sieht ohne Zweifel so aus wie unten links gezeigt. |
| |
 |
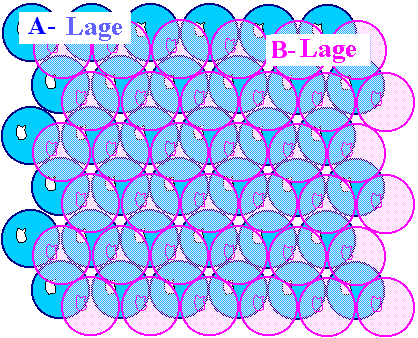 |
| Dicht gepackte Atomlage auf einer Ebene |
Die zweite dicht gepackte Atomlage |
|
|
 |
Danach legen wir einfach die nächste Atomlage auf die schon vorhandene erste Lage. Die
Atome wollen möglichst dicht zusammenhocken; damit sitzen die Atome der 2. Lage ganz natürlich in den Kuhlen
der 1. Lage; so wie oben rechts gezeigt. |
|
 |
Um die Lagen auseinanderhalten zu können, nennen wir die erste Lage die "A"-Lage,
die zweite Lage die "B"-Lage. |
 |
Und so weiter. Die 3. Lage kommt auch wieder "auf Kuhle". |
|
 |
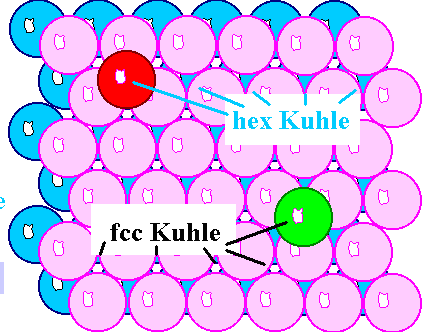
Ja, schon – aber auf welche? Wenn wir genau hinschauen, gibt es jetzt zwei
grundsätzlich verschiedene Kuhlensorten, wie unten links gezeigt. |
| |
 |
 |
| Die zwei Kuhlensorten der zweiten Lage |
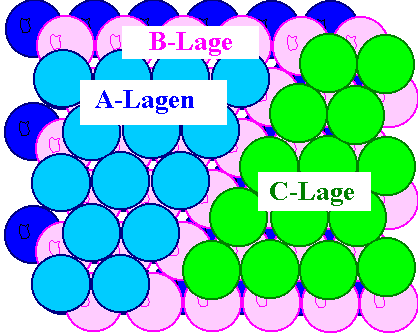
Die zwei möglichen Stapelfolgen |
|
|
 |
Unterhalb der "hex-Kuhlen" liegt ein Atom
der A-Lage, unterhalb der "fcc-Kuhlen" liegt eine Kuhle der
A-Lage. Wenn wir das nicht berücksichtigen, sondern einfach an verschiedenen Stellen mal ein Atom der dritten
Ebene draufpacken (wie oben rechts gezeigt) und dann weitermachen, wird es ein Problem geben – wie oben rechts gezeigt. |
 |
Falls wir Atomlagen, die exakt übereinandersitzen, den gleiche Buchstanben
geben, haben wir die Stapelfolgen ABA... und ABCAB... realisiert, denn im Bild oben links müssen wir
den grünen Atomen einen eigenen Buchstaben als Lagenkennzeichnung geben; sie liegen nicht
über den A- oder B-Lagenatomen. |
 |
Wie geht's weiter? In Prinzip könnte man jede Stapelfolge machen, die eine
Kopf-auf-Kopf-Situationen vermeidet, also zum Beispiel ABCABACBABCABAC...; nicht aber zum Beispiel ABCAABCCB....
Das ist dann aber möglicherweise kein Kristall mehr, falls es "nach oben" keine Periodizität mehr gibt.
(Mit unterschiedlich großen Perioden kommt sowas in der Natur aber durchaus vor, siehe z.B. die vielen Polytypen
des SiC [vgl. hier]!) |
|
 |
Mutter Natur hat es oft (aber nicht immer) einfach und ordentlich und macht deshalb (fast) nur diese Stapelfolgen:
- ABABABAB... = "Hexagonal close packed" (hcp): Kristall gebildet
aus dem hexagonalen Gitter mit zwei Atomen in der Basis
(bei (0,0,0) und bei (S,S,½ )).
- ABCABCABC... = fcc-Gitter mit einem Atom in der Basis.
|
|
 |
Es ist automatisch klar, dass die Packungsdichte (= durch
Kugeln besetztes Volumen der Elementarzelle in %) in beiden Fällen exakt gleich ist - es sind 74 %. Mehr
geht nicht – weniger schon. Ein bcc-Kristall mit einem Atom in der Basis liegt zum Beispiel bei 68 %. |
|
 |
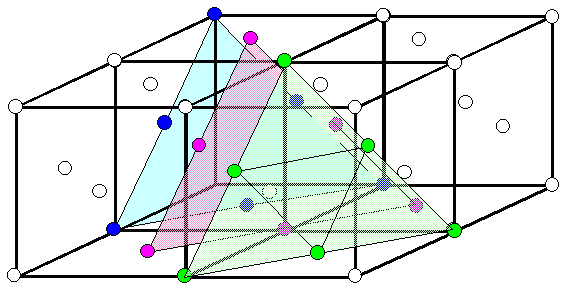
Wer die Übungsaufgabe schon gemacht
hat, weiß, warum das so ist. Wer die Aufgabe nicht gemacht hat, schaut sich das Bild unten an und kommt selbst zum
Schluss, dass die ABCABC...-Stapelfolge wie oben gezeichnet nichts anderes ist als ein Blick auf die {111}-Ebenenschar
des fcc-Kristalls. |
| |
|
 |
Mit einem Atom in der Basis des fcc-Gitters,
das dann auf den Ecken und Seitenmitten des Würfels sitzt, kristallieren z.B. Al, Ni, Cu, Pd,
Ag, Pt, Au sowie alle Edelgase. Das deckt etwas weniger al 30 % der Elemente ab. Etwa 35
% aller Elemente kristallisieren in einem hcp-Kristall, darunter beispielsweise Mg, Re, Co,
Zn, Cd, C (als Graphit), aber auch z.B. N bei tiefer Temperatur. |
|
 |
Das ist eigentlich klar, denn z.B. alle Metalle sollten wegen ihrer ungerichteten Metallbindung
automatisch in einer dichtesten Kugelpackung
kristallisieren. |
 |
Zwei Fragen dürfen sich jetzt aufdrängen:
- Warum tun das nicht alle? Was hindert die ca. 30 % der Elementmetalle im
Periodensystem (z. B. K, Rb, Cs, V, Nb, Ta, Cr, Mo und W)
daran, in einer dichtesten Kugelpackung zu kristallisieren?
- Nach welchen Kriterien wählt Mutter Natur zwischen den beiden dichtesten Kugelpackungen aus? Warum hat Nickel (Ni)
die fcc-Struktur, das sehr ähnliche Kobalt (Co) aber die hexagonale?
|
 |
Die Antwort ist nicht einfach – wir werden später darauf zurückkommen.
Es hat etwas mit Entropie zu tun, dem Grad der Unordnung, und damit auch etwas mit der
Temperatur. |
|
 |
Mutter Natur macht die Sache sogar noch spannender: Nicht ganz wenig Metalle ändern ihre
Kristallstruktur mit der Temperatur. Zwei Beispiele:
- Eisen (Fe): Schmelzpunkt (1535
oC) – 1402 oC: bcc;
1402 oC – 910 oC: fcc;
910 oC – 273 oC: bcc.
- Kobalt (Co): Schmelzpunkt (1495
oC) – 440 oC: fcc;
440 oC – 273 oC: hcp. |
|
 |
Das ist nicht nur "interessant", sondern hat gewaltige technische Konsequenzen für
die "metal bending industry"! Da uns die aber nicht so toll interessiert, gehen wir hier nicht darauf ein. |
| |
|
 |
Hier noch eine etwas anspruchsvollere Übung zur dichtesten Kugelpackung im
fcc-Gitter: |
| |
|
| |
|
© H. Föll (MaWi für ET&IT - Script)