 |
Kristall = Gitter + Basis |
|
Kristall = regelmäßige Anordnung
von identischen Bausteinen
|
| Kristall |
= |
Gitter |
+ |
Basis |
 |
= |
 |
+ |
 |
fcc (1 Atom in Basis) und hcp = dichteste Kugelpackungen
Packungsdichte ca. 74
%
Etwa 2/3 aller Elemente
Rest meist bcc
|
|
|
 |
Gitter: Periodische Punktfolge im Raum |
|
|
 |
Definiert durch drei Basisvektoren
a i und Translationsvektor
T = ua1
+ va2 + wa 3
; u, v, w = Integer | |
|
 |
Basis = Minimal 1 Atom bis zum komplexen Atomverbund |
|
 |
Wichtige Gitter: | |
| |
| |
| |
| |
|
| |
|
|
 |
Kubisch flächen- und raumzentriert (fcc und
bcc ; oben) und hexagonal (hex
, unten; links Grundgitter, rechts mit zusätzlichen Gitterpunkten für dichteste Kugelpackung, hcp) |
|
|
| |
| |
 |
Mit Miller-Indizes werden Richtungen und Ebenen definiert und beschrieben. |
|
Richtung: Kleinste Integers des Vektors,
<u, v, w> allgemeine Richtung
[u, v, w] spezifische Richtung
Ebene: Ganzzahlige reziproke Schnittpunkte mit Achsen,
{h, k, l} allgemeine Ebene
(h, k, l) spezifischen Ebene |
| dhkl = | a
(h2 + k2 + l2)1/2
|
|
|
| |
| |
| |
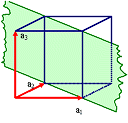 | Kubisches Gitter;
Schnittpunkte bei
1, 1, ¥
Indizes
(110) |
| |
|
| |
|
|
 |
Mit Miller-Indizes kann man rechnen. |
|
| |
| |
| |
 |
Einkristalleigenschaften sind anisotrop (außer
die kubischer Gitter). | |
| Polykristalle sind isotrop |
|
© H. Föll (MaWi für ET&IT - Script)


