|
Wir werden jetzt relativ zügig die in Kapitel 4 gewonnenen Erkenntnisse anwenden
und vor allem quantitative Betrachtungen anstellen. |
|
 |
Die entscheidende Größe für die Leitfähigkeit war die Dichte
an beweglichen Ladungsträgern im Valenz- und Leitungsband. Bei Halbleitern
ist sie bei T = 0 K gleich Null. |
|
 |
Bei endlichen Temperaturen wird die thermische Energie
ausreichen, um einige Elektronen vom Valenzband ins Leitungsband zu befördern,. Diese werden zwar nach nach Ablauf
der Lebensdauer wieder rekombinieren, aber die thermische
Generation erzeugt ja auch ständig wieder neue Elektron-Loch Paare. |
|
 |
Zwischen Generation und Rekombination wird sich ein thermisches Gleichgewicht
einstellen, mit (im Mittel) konstanter Konzentration an Elektron-Loch Paaren. Und für das thermische Gleichgewicht
in intrinsischen
Halbleitern haben wir fertige Formeln! |
 |
Der Terminus "intrinsisch" steht
hier wie zuvor für "ohne
Hilfe von außen". Damit ist schlicht und einfach gemeint, daß wir über ideale, perfekte
Kristalle sprechen, deren Eigenschaften "von innen" kommen, d.h. immer da sind.
|
 |
Wir ventilieren jetzt nämlich ganz offenbar die Frage, wieviele der Plätze
(= Zustände) im Leitungsband bei der Temperatur T besetzt sind. Die Antwort darauf gibt immer dieselbe
Fundamentalformel: |
|
 |
Die Zahl (oder Volumendichte) n(E,T)
der besetzten Plätze bei der Temperatur T und Energie E pro Energieintervall DE
ist gegeben durch: Zustandsdichte D(E) mal Fermiverteilung f(E,T). |
| |
| ne(E, T) = D(E)
· f(E, T) ·DE |
|
|
 |
Das "oder Dichte" bezieht sich immer darauf,
ob wir die Zustandsdichte als Zustände pro Energieintervall (entpricht Zahl), oder
pro Energieintervall und Volumenelement (entspricht Dichte) angeben. |
|
 |
Die Gesamtzahl (oder Dichte) nL(T)
aller Elektronen im Leitungsband ist dann |
| |
| neL(T) = |
¥
ó
õ
EL |
D(E) · f(E, T) · dE |
|
|
|
 |
Dabei ist EL die Energie der Leitungsbandkante. |
|
 |
Wir haben schon eine kleine Näherung eingebaut, weil wir bis ins Unendliche integrieren
statt bis an die obere Leitungsbandkante. Aber weiter oben im Leitungsband drückt die Fermiverteilung sowieso alles
auf Null, die obere Integrationsgrenze ist damit unerheblich. |
 |
Wir haben jetzt zwei Probleme |
|
 |
Wir kennen die wirkliche Zustandsdichte des jeweiligen Materials nicht, und falls wir sie
kennen würden, wäre das Integral nur noch numerisch zu knacken (man betrachte z.B die Zustandsdichte
von Ge). |
|
 |
Wir kennen die Fermienergie
EF (noch) nicht. |
 |
Aber das sind Scheinprobleme, die wir einfach lösen können: Wir nehmen
1. als Näherung für die Zustandsdichte die Zustandsdichte
des freien Elektronengases (normiert auf E – EL)
, und lassen 2. die Fermienergie als freien Parameter einfach erst mal stehen. |
|
 |
Damit erhalten wir |
|
|
| neL(T) = |
¥
ó
õ
EL |
æ
ç
è |
(2me)3/2
2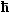 3p2 3p2 |
· (E – EL)1/2 |
ö
÷
ø | . |
æ
ç
è | exp
| æ
è |
E – EF
kT |
ö
ø | + 1 |
ö
÷
ø |
–1 | · dE |
|
|
 |
Das sieht auch noch nicht so prall aus, obwohl man dieses bestimmte
Integral vielleicht sogar exakt lösen könnte - wer weiß? Wir werden jetzt wird natürlich nähern: |
|
 |
Statt
f(E,T) nehmen wir die Boltzmann-Näherung,
d.h. wir setzen f(E,T) » exp–(E – EF)/kT.
Das können wir machen falls EL
– EF » kT. Dann erhalten wir |
| |
| neL(T ) = |
(2me)3/2
2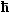 3p2 3p2 |
¥
ó
õ
EL |
(E – EL)1/2 . | exp –
| E – EF
kT |
· dE |
|
|
|
 |
Das sieht nicht nur lösbar aus, das ist auch lösbar - aber auch nur mit viel Mühe! |
 |
Helfen wird, daß es Nicht-Mathematikern nicht verboten
ist, bei der Lösung einer Matheaufgabe physikalisch zu denken. Hier überlegen wir erst mal, was die entscheidende
Variable für die Ladungsträgerkonzentration bei einer gegebenen Temperatur sein wird. |
|
 |
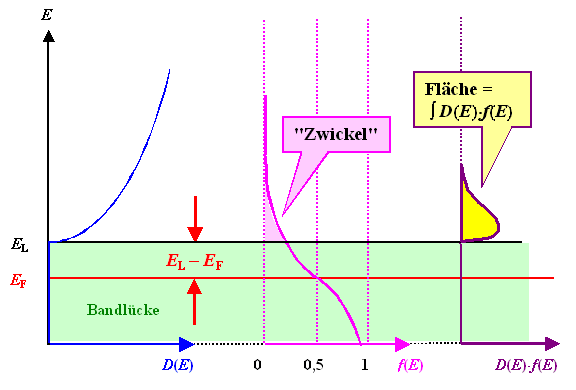
Dazu stellen wir die Integrationsaufgabe mal graphisch dar. |
| |
|
|
 |
Wir haben links die Zustandsdichte des freien Elektronengases, in der Mitte die Fermiverteilung,
und rechts das Produkt aus beiden. Die Fläche unter dieser Kurve gibt den Wert
des bestimmten Integrals. |
|
 |
Falls wir gedanklich die Zustandsdichte durch die wirkliche
Zustandsdichte ersetzen, wird das den Wert des Integrals etwas ändern. Die wirkliche
Zustandsdichte ist aber eine Art Materialkonstante, damit nicht variabel, und für den Wert des Integrals als Funktion
von z.B. der Temperatur nicht so wichtig. |
|
 |
Die entscheidende Größe, die den Wert des Integrals
massiv beinflussen kann, ist ganz klar die Größe des im Leitungsband liegenden
"Zwickels" der Fermiverteilung. Damit ist - immer bei gegebener Temperatur - der Abstand
der Fermienergie von der Leitungsbandkante die entscheidende Variable. |
 |
Man wird also jetzt und in künftigen Fällen gut daran tun, EL
– EF als neue Variable einzuführen. |
|
 |
Das ist einfach. Wir setzen E – EF = E – EL
– (EF – EL); außerdem erweitern wir den (E – EL)1/2 Term mit (kT)½/(kT)½ und ziehen ein
(kT)½ vor das Integral - damit haben alle Energieterme die gleiche Form. Dann machen wir noch
die naheliegende Substitution |
| |
E – EL
kT |
= x | |
dE = kT · dx |
|
|
|
 |
Alles zusammen eingesetzt in das Integral (und das zusätzliche kT aus dem
dx vorgezogen) ergibt |
|
|
| neL(T) = | |
(2me · kT)3/2
2p2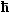 3 3 |
· | exp |
æ
ç
è |
– | EL – EF
kT | ö
÷
ø
| · |
¥
ó
õ
0 |
x½ | · |
e –x |
· dx |
|
|
|
 |
Das verbleibende bestimmte Integral ist (immer noch mit Mühe) lösbar, sein Wert
ist ½ · p½ - also wie
gehabt dicht bei 1. |
 |
Wir erhalten schlußendlich (wer's nicht glaubt, muß
nachrechnen) |
| |
| neL(T) = |
æ
ç
è |
me · kT
21/3 · p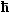 2 2 |
ö
÷
ø |
3/2 | · exp – |
EL – EF
kT |
= | const. · T
3/2 · exp – |
EL – EF
kT |
|
|
|
 |
oder, falls wir was üblich ist, 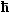 durch h/2p
ersetzen: durch h/2p
ersetzen: |
| |
| neL(T) = 2 · |
æ
ç
è |
2p · me · kT
h2 | ö
÷
ø
| 3/2 | · exp – |
EL – EF
kT |
= | const. · T
3/2 · exp – |
EL – EF
kT |
|
|
 |
Das ist ein fundamentales Ergebnis! Es sagt aus, daß wir fast - bis auf
den Faktor T
3/2 - eine altbekannte Arrheniusbeziehung
haben. |
|
 |
In der Konstanten steckt im wesentlichen die Zustandsdichte
des freien Elektronengases. Man kann diesen Vorfaktor natürlich ausrechnen (Mit T in K
eingesetzt) und erhält |
| |
| neL(T) = |
4.59 · 1015 · T 3/2 · exp – |
EL – EF
kT |
cm–3 |
|
|
| | |
|
|
Konzentration der Löcher im Valenzband |
| | |
 |
Nachdem wir jetzt die Konzentration der Elektronen im Leitungsband kennen, fragen
wir uns, wie groß ist nV, die Konzentration der Löcher im Valenzband? |
|
 |
Die Antwort ist natürlich sehr einfach: Genauso groß wie die Konzentration der
Elektronen im Leitungsband, denn für jedes Elektron im Leitungsband ist ja genau ein Loch in Valenzband entstanden. |
|
 |
Nun stellen wir uns aber kurz mal unwissend und fragen, wie man nV
ausrechnen würde, falls man nL nicht schon kennt. Die
Antwort muß lauten |
|
 |
Die Zahl (oder Volumendichte) n(E,T)
der nichtbesetzten Plätze (= Löcher) bei
der Temperatur T und Energie E pro Energieintervall DE
ist gegeben durch: Zustandsdichte D(E) der Elektronen mal Wahrscheinlichkeit für Nichtbesetzung
(= 1 – f(E, T)). In Formeln: |
| |
| nh(E, T) = D(E)
· [1 – f(E, T)] · DE |
|
 |
Die Auswertung läuft sehr ähnlich zum Fall der Elektronen,
wir erhalten für die Löcherdichte nhV(T) im gesamten Valenzband
|
| |
| nhV(T) = |
EL
ó
õ
–¥ |
D(E) · [1 – f(E, EF,
T)] · dE = 4.59 · 1015 · T
3/2 · exp – |
EF – EV
kT | cm–3 |
|
|
 |
Der einzige Unterschied ist, daß die im Boltzmannfaktor wirksame Energiebarriere
jetzt durch EF – EV gegeben ist; dem Abstand der Fermienergie von der Valenzbandkante. |
|
 |
Das ist aber auch zu erwarten; wir können ja exakt die gleiche Überlegung, die wir
für die Elektronen im Leitungsband schon durchgeführt haben, auch für die Löcher im Valenzband machen. |
 |
Zwei Fragen drängen sich jetzt auf |
| |
1. Wie groß ist die Fermienergie EF ? Ohne eine Zahl
können wir nichts ausrechnen - wir wissen noch nicht einmal ob die Boltzmann-Näherung
überhaupt berechtigt war. |
|
 |
2. Wie groß ist der Einfluß des T
3/2 - Terms? In anderen Worten, wie groß ist bei realen Hableitern die Abweichung der log (nL)
über 1/T Kurve von einer Arrheniusgeraden? |
 |
Die zweite Frage läßt sich beantworten, nachdem wir die erste geklärt
haben. Wir widmen uns deshalb jetzt zum ersten mal einer der Zentralfragen der Halbleitertechnologie:
|
|
 |
- Wo liegt (im Banddiagramm) die Fermienenergie?
- Was genau bestimmt die Lage der Fermieenergie?
- Wie kann ich sie ausrechnen
|
|
 |
Wir werden uns diese Frage mehrmals stellen. Die erste Antwort wird im nächsten Unterkapitel
gegeben. |
| |
|
© H. Föll (MaWi 2 Skript)