3.5.2 Elektronenmikroskopie

	Ein Elektronenstrahl ist nicht nur eine (gute Näherung an eine) ebene Welle, sondern - im Gegensatz zu Röntgen- und Neutronenstrahlen - auch ein elektrischer Strom geladener Teilchen.
		Damit kann der Strahl durch elektrische und/oder magnetische Felder abgelenkt werden - und das eröffnet die Möglichkeit elektromagnetische Linsen zu bauen.
		Obwohl aus sehr prinzipiellen Gründen nur Sammellinsen möglich sind, kann man damit trotzdem ein Mikroskop bauen - ein Elektronenmikroskop.
	Elektronenmikroskope kommen in zwei grundverschiedenen Varianten:
	1. Das Rasterelektronenmikroskop (REM oder englisch SEM für "Scanning Electron Microscope") "rastert" lediglich einen mit elektromagnetischen Linsen fein fokussierten Elektronenstrahl im Zick-Zack über die Probe (wie im CRT Bildschirm). Registriert wird in einem geeigneten Detektor, wieviele Sekundärelektronen (oder sonstwas) freigesetzt werden.
		Das Bild ist im wesentlichen eine "dreidimensionale" Wiedergabe der Oberflächentopographie, mit einer Schärfentiefe und Auflösung, die um Größenordnungen besser ist als im Lichtmikroskop. Der Link führt zu Beispielen.
		REMs haben noch sehr viel mehr Anwendungsmöglichkeiten - sie machen aber grundsätzlich nicht von der Wellennatur des Elektronenstrahls Gebrauch und sollen uns hier nicht weiter interessieren.
	2. Das Transmissionselektronenmikroskop (TEM). Hier wird der Elektronenstrahl möglichst ohne Absorption durch die sehr dünne Probe geführt und was immer unten herauskommt durch elektromagnetische Linsen auf einen Bildschirm abgebildet. Dabei hat man durch einfaches Umschalten immer zwei Möglichkeiten:
	1. Man erzeugt ein Beugungsbild. Das ähnelt dann dem Beugungsbild einer Laue-Aufnahme in Transmission - obwohl die Welle hier monochromatisch ist.
		Dass trotzdem sehr viele Reflexe angeregt werden liegt daran, daß k sehr lang ist, so daß die Ewaldkugel praktisch als Ebene durchs reziproke Gitter der Probe läuft und alle reziproken Gitterpunkte schneidet die in einer Ebene senkrecht zum Elektronenstrahl liegen. Da die reziproken Gitter"punkte" bei sehr dünnen Proben eher ausgedehnt sind, trifft die Ewaldkugel relativ viele davon.
		Das nachfolgende Bild zeigt einige Beispiele dessen was man auf dem Bildschirm zu sehen bekommt.
		Al Einkristall Schichtfolge Si - NiSi - NiSi2 Epitaktisches Wachstum, d.h. Einkristallinität bleibt weitgehend erhalten Schichtfolge Si - NiSi; das NiSi ist weitgehend polykristallin Polykristallines PtSi
		Die Bilder lassen sich selbstverständlich quantitativ auswerten; auch damit ist eine Strukturbestimmung möglich.
	2. Man erzeugt ein Bild der an der Unterseite der Probe lokal vorhandenen Intensität Ig eines gebeugten Strahls, oder des Primärstrahls dessen lokale Intensität einfach (I0 – gesamte lokal gebeugte Intensität) sein muß.
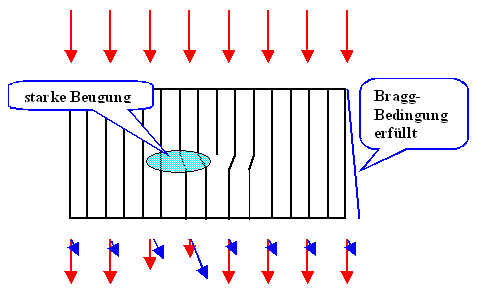
	Mit der zweiten Variante kann man Kristallgitterdefekte abbilden, wir schauen uns das mal schematisch für eine Stufenversetzung an.
		Zunächst orientieren wir die Probe mit einer Stufenversetzung wie gezeigt relativ zum Elektronenstrahl derart, daß die Bragg-Bedingung für die gezeichneten Ebenen fast, aber nicht exakt erfüllt ist. Der blaue Strich deutet an, wie die Probe orientiert sein müßte, damit die Bragg-Bedingung exakt erfüllt ist. Die Zeichnung übertreibt mächtig.
		Um die Versetzung herum ist das Gitter lokal verbogen; in dem angedeuteten Bereich ist die Bragg Bedingung erfüllt, oder jedenfalls besser erfüllt, als weg von der Versetzung.
		Damit wird an der Unterseite der Probe, entlang der Projektion der Versetzungslinie, viel Intensität des einfallenden Elektronenstrahls in den abgebeugten ("blauen") Strahl "umgeleitet" (und zwar immer nur auf einer Seite der Versetzung).
		Mit einer geeignet plazierten Blende kann man den gebeugten Strahl ausblenden und ein stark vergrößertes Bild der Intensitätsverteilung des Primärstrahls an der Unterseite der Probe machen. Die Versetzung wird dann als leicht verschwommene dunkle Linie erscheinen.
		Da die Auflösung eines Mikroskops - d.h. die Größe der kleinsten noch beobachtbaren Strukuren - immer in der Größenordnung der Wellenlänge der verwendeten Strahlung liegen, ist bei Lichtmikroskopen bei etwa 0,5 µm das Ende der Fahnenstange erreicht. Elektronenmikroskope verwenden typischerweise Beschleunigungsspannungen von 100 kV - 1,5 MeV und können damit ohne weiteres atomare Auflösung im nm Bereich erreichen (es ist die Qualität der elektomagnetischen Linsen, nicht die Wellenlänge, die hier problematisch wird).
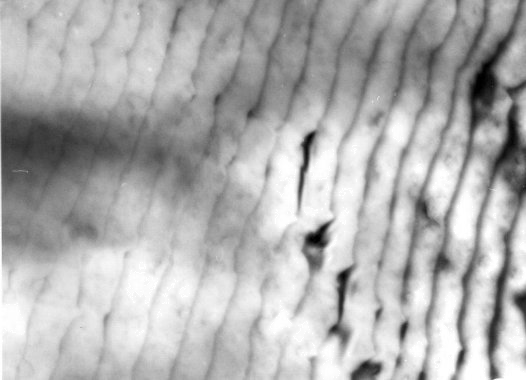
	Genauso ist es auch - das nachfolgende Bild zeigt ein Beispiel
		Wir sehen eine ganze Schar von (ungefähr parallelen) Versetzungen. Die Probe ist leicht verbogen; links sind wir relativ weit weg von der exakten Bragg-Bedingung, rechts dicht dran. Der Versetzungskontrast nimmt von links nach rechts deutlich zu; gleichzeitig werden die Linien breiter und unschärfer, wie wir das erwarten würden.
	Das TEM ist ein außerordentlich mächtiges Intrument zur Strukturbestimmung mit lokaler Auflösung. Man kann kleinste Defekte (bis hinunter zu einzelnen Atomen) sichtbar machen und analysieren.
		Allerdings ist es nicht ausgesprochen billig (Standardgeräte so um 1 Mio €; Spitzengeräte um die 7 Mio €), schwer zu bedienen (man braucht, typischerweise im Rahmen einer Doktorarbeit so 1 - 2 Jahre bevor man TEM "kann"), und nur einsetzbar für winzigste Pröbchen!
		Atome sind einfach klein. Das gesamte bisher weltweit mit TEM untersuchte Probenvolumen liegt deutlich unter 1 mm3
	Mehr zum TEM in Kurzfassung im Link. Wer es noch genauer wissen will (und viele Beispiele anschauen möchte), geht zum entsprechenden Kapitel im Hyperskript "Defects"

© H. Föll (MaWi 2 Skript)