Porengitter und Radiale Verteilungsfunktion in InP

	In vielen Halbleitern kann man durch geeignete elektrochemische Ätzverfahren kleine Löcher oder Poren ätzen - wie das genau funktioniert ist nicht besonders gut verstanden und Gegenstand laufender Forschung.
		Typische Poren haben Durchmesser um 1 µm herum, und können viele 100 µm tief werden. Normalerweise sind sie regellos verteilt, bilden also eine Art amorphe Struktur wie im Rückgrat gezeigt - wir müssen nur statt der Kugeln = Atome jetzt Poren (von oben gesehen) vorstellen.
		Eine ganz heiße Entdeckung wurde 2001 von Sergiu Langa gemacht; ein Doktorand am Lehrstuhl, als es ihm gelang besonders schöne Poren mit selbstorganisierter Kristallinität in InP zu ätzen. Dies ist im untenstehenden Bild gezeigt.
	Hier noch, weil es so ein tolles Bild ist, ein Bruch quer durch die Poren
	Ist das jetzt ein Kristall? Der vergrößerte Ausschnitt im ersten Bild sieht jedenfalls streckenweise sehr danach aus.
		Aber so ganz paßt das Bild nicht zur strengen Definition "Aus der bekannten Position einiger Atome läßt sich die Position aller anderen Atome berechnen".
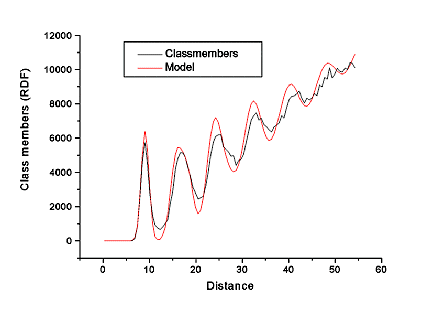
		Schauen wir uns also die radiale Verteilungsfunktion an:
		Die schwarze Kurve zeigt die Meßwerte; die rote ist ein Fit und hier nicht interessant.
	Was wir sehen ist, daß man von einem beliebigen Nullpunkt ausgehend, zwar keine Aussagen mehr machen kann wo man weit weg eine Pore finden wird, aber immerhin noch bis zum 5. und 6. Nachbarn eine Nahordnung vorhanden ist.
		In der Praxis reicht das um von einem Porenkristall zu reden! Natürlich ist es ein Polykristall, aber wir haben keine amorphe Anordnung.
	Die spannende Frage ist natürlich: Warum? Warum wachsen überhaupt Poren, warum werden die Poren alle ungefähr gleich groß, und warum ordnen sie sich halbwegs regelmäßig an?
		Wie wissen sie voneinander, denn nur durch irgendeine Wechselwirkung zwischen den Poren kann eine solche selbstorganisierte Struktur entstehen.
	Noch eine Frage: Wie, um nagelneue Forschung (2002) einzubringen entsteht ein Poreneinkristall - hier gezeigt:
	Zugegeben, kein besonders toller Einkristall; er ist voller Defekte.
		Das es aber tatsächlich ein Einkristall ist - der erste seiner Art übrigens - erkennt man, wenn man einer Gitterrichtung über größere Distanzen folgt wie mit der schwarzen Linie angedeutet.
	Die Forschung geht weiter: Mit optimierten Bedingungen kann man jetzt (Anfang 2003) schon einen recht guten Einkristall herstellen, bei dem dei Einkristallinität auch sofort ins Auge sticht:
	Die Forschung geht weiter.....
		Herrn Lölkes, ebenfalls Doktorand am Lehrstuhl, ist es gelungen (Mitte 2003).die InP Verhältnisse auf Silzium zu übertragen. Aber nur im Prinzip. Im Detail erguibt sich etwas völlig neues, wie unten gezeigt
	Wir haben einen sogenannten "frustierten Kristall", eine spezielle Struktur, die bisher allenfalls einigen Mineralogen und Magnetikern bekannt war.
		Kurz gesagt, können sich die Poren nicht entscheiden, ob sie ein quadratisches oder hexagonales Gitter bilden wollen; die Ausschnitte zeigen entsprechende Detailstrukturen.
		Die Gesamtstruktur ist nun aber nicht amorph, sondern zeigt eine spezielle radiale Verteilung; dies ist in der "Autokorrelationsfunktion" sichtbar (eine Art zweidimensionale radiale Verteilungsfunktion; Einsatz oben): Die nächsten Nachbarn sind kaum miteinader korreliert, (gleichförmiger heller Ring um Zentrum), wohl aber die zweitnächsten (10 helle und zwei nicht so helle Maxima im zweiten Ring).

Mit Frame

Simulation der Anodischen Auflösung von Silizium

3.1.1 Allgemeines zu Kristallen und amorphen Festkoerpern

© H. Föll (MaWi 1 Skript)