|
Transmission electron microscopy
(TEM)
is by far the most important technique for studying defects in great detail. Much of what was stated before about defects
would be speculative theory, or would never have been conceived without TEM. |
 |
Using TEM, we look through a piece of material with electron "waves,"
usually at high magnification. |
|
 |
In contrast to X-ray imaging, lenses for electron beams exist: Magnetic fields (and,
in principle, electric fields, too) can be made with gradients that act as convex lenses for the electron waves. For very
general reasons it is not possible to construct electromagnetic concave lenses and that means that imaging systems are not
very good because lens aberrations cannot be corrected as in conventional optics. |
|
 |
Still, the intensity distribution of the electron waves leaving the specimen can
be magnified by an electron optical system and resolutions of » 0,1 nm are attainable. |
|
 |
The electrons interact with the material in two ways: inelastic and elastic scattering.
Inelastic scattering (leading eventually to absorption) must be avoided since it contains no local information. The electron
beam then will be only elastically scattered, i.e. diffracted; the lattice and the defects present modulate amplitude and
phase of the primary beam and the diffracted beams locally. |
|
 |
The energy of the monochromatic electron beam is somewhere between (100 - 400)
keV, special instruments go up to 1,5 MeV (at a price of ca. 8 M€). Keeping inelastic scattering
of the electrons small has supremacy, this demands specimen thicknesses between 10 nm to ca. 1 µm. The
resolution depends on the thickness; high-resolution TEM (HRTEM) demands specimens thicknesses in the nm region. |
 |
This has a major consequence: The total volume of the material investigated by
TEM since it started in the fifties, is less than
1 cm3! |
|
 |
Taking and interpreting TEM images is a high art; it takes several years
of practice. The major part of any TEM investigation is the specimen preparation. Obtaining specimens thin enough
and containing the defects to be investigated in the right geometry (e.g. in cross-section) is a science in itself. |
|
 |
Still, practically all detailed information about extended defects comes from TEM investigations
which do not only show the defects but, using proper theory, provide quantitative information about e.g. strain fields. |
 |
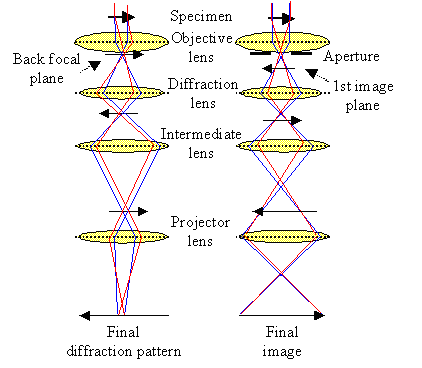
The key is the electron-optical system. It not only serves to magnify the intensity
(and, in HRTEM, the phase) distribution of the electron waves of the electron waves leaving the specimen, but, at
the throw of a switch, provides electron diffraction patterns. The picture shows the basic electron-optical design of a
TEM |
| |
| |
|
 |
At least four (usually five) imaging lenses are needed in addition to two condenser lenses (not shown).
For most imaging modes an aperture right after the objective lens must be provided. |
 |
The beam paths for the diffraction mode and the imaging mode are shown on the left. |
 |
The most important lens is the objective lens. Its resolution limit
defines the resolution of the whole microscope. |
 |
The aperture after the objective lens is essential for the conventional imaging modes. It is usually set
to only admit the primary beam, or one of the diffracted beams into the optical system. |
| | |
| |
 |
The image, or better, the contrast of a dislocation
depends on several parameters. Most important are: |
|
 |
The diffraction conditions.
Is the Bragg condition fulfilled for many reciprocal lattice vectors g, for none, or just for two? All cases
are easily adjusted by tilting the specimen relative to the electron beam while watching the diffraction pattern. The preferred
condition for regular imaging is the "two-beam" case with only one "reflex" excited; i.e. the Bragg
condition is only met for one point in the reciprocal lattice or one diffraction vector
g (usually with small Miller indices, e.g. {111} or {220}. |
|
 |
The excitation error: Is the Bragg condition
met exactly (excitation error = 0; dynamical case) or only approximately (excitation error < 0 or >
0; kinematical case). |
|
 |
The magnitude of the scalar product between the reciprocal lattice vector g
and the Burgers vector b, g · b. If it is zero or very small, the contrast is weak, i.e.
the dislocation is invisible. |
|
 |
The imaging mode. Is the primary beam admitted
through the aperture and used for imaging (bright field condition), or a diffracted beam
(dark field condition)? In other word, is it the intensity distribution of the primary beam
or of a diffracted beam that constitutes the image? Or are several beams used whose interference produces a high-resolution
image? |
 |
How is the proper diffraction condition selected experimentally? Fortunately,
a little bit of inelastic scattering produces so-called Kikuchi
lines which provide a precise and easily interpretable guide to the exact diffraction condition obtained by tilting the
specimen. The link shows examples. |
|
 |
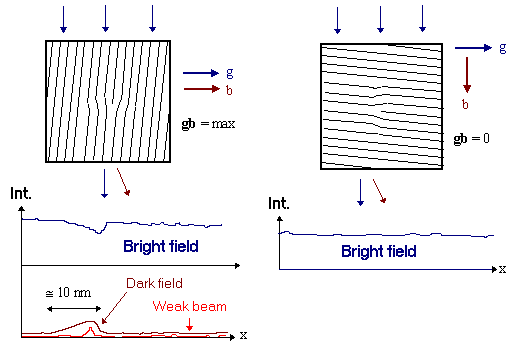
The following picture illustrates some imaging conditions for dislocations with maximum and
minimum gb product. |
|
|
|
 |
We may draw the following conclusions; they are justified by the full theory of
TEM contrast. |
|
 |
Dislocations are invisible or exhibit only weak contrast if g · b
= 0. This can be used for a Burgers vector analysis by imaging the same
dislocation with different diffraction vectors and observing the contrast. |
|
 |
Under kinematic bright field conditions (Bragg condition met almost, but not quite),
the dislocation is imaged as a dark line on a bright background. The width of the line corresponds to the width of the region
next to one side of the dislocation where the Bragg condition is now met; which is usually several nm. |
|
 |
Under dark field conditions the dislocation appears bright on a dark background. |
|
 |
Under dark field conditions with large excitation errors the Bragg condition is
only met in a small region close to the core of the dislocation. The image consists of a thin white line on a pitch black
background. This is the so-called "weak-beam" condition; it has the highest resolution
of conventional imaging modes. It is hard to use, however, because almost nothing is seen on the screen (making adjustments
difficult) and long exposure times are needed which are only practical with a very stable instrument. |
© H. Föll (Defects - Script)