12.4.3 Hitting Something

We are finally ready to hit something with our sword. But before I teach you the physics of hitting, I must remind you of a simple truth from long begone days, back in chapter 2.1:

Swords are evil objects if you consider only
their intended or actual use as weapons.

Nothing has changed. There is no reason to hit other living beings with the sharp edge of your sword. Forget it. You are not the chosen one who has to redeem this or that, nor are you the special hero who in his spare time rescues those maidens in distress. Dragons count as endangered wildlife and are heavily protected anyway.
There are, however, good reasons for hitting balls with tennis rackets, golf clubs, baseball bats and so on. There are equally good reasons to whack at each other in simulated sword fights with practice swords. Mankind needs to play and that includes swordplay for fun. Keep that in mind when you read what follows.

When your sword hits something it will do so at some point on the blade, let's call that the impact point. Of course, in principle you could hit a planar target with a length of the blade and not just with a point but that would not be a good strike. Curved blades are curved after all, to make initial contact with the target on a point.
Equally of course you may not hit a point on the target with a point on your blade but deliver a thrust with the tip of your blade. I'm not going into that because the physics of stabbing is rather simple. You stab a target much softer than your blade and you penetrate it, or you stab a target about as hard or harder than your blade and you brake your blade (and possibly your wrist).

As far as hitting is concerned, we need to look at the physics of collisions or impacts . This part of mechanics is governed by the conservation law of (linear and angular) momentum plus the conservation law of energy. It is not all that complicated but a certain amount of math does come into play. The kind of collision that relates to sword strokes will require the solving of 11 equations with 11 unknowns, for example. I'll do that in special module, here we will start with what we already know without solving equations.

The somewhat idealized situation we are going to look at is shown below. We swing our sword as shown, with an apparent center of rotation somewhere around the elbow. It is roughly what that Samurai is doing at that point in time when his katana is about horizontal. The sword (plus parts of you) rotates with some angular velocity expressed by its circular frequency w that gives the impact point a linear velocity v. The target is something with some mass m_T, an arbitrary shape in reality but a circle in the picture for ease of drawing. The target is also mobile. Not only can it be moved, it might even have some initial speed of its own (not shown in the drawing). Think of a tennis ball flying towards you, for example. The target also has some properties that will come into play later.


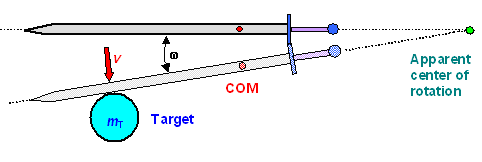How we look at hitting something

Now let's recapitulate the things you definitely know, even if you are more mathematically challenged than the average banker or USA president. You know what you want to do with some target. It should look like this:



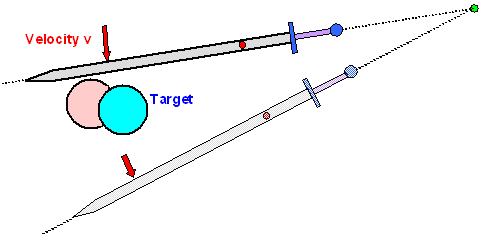Producing "good" target damage

You want to run your sword right through the target, neatly cleaving it in two parts. Your sword keeps moving but with reduced speed. Alternatively, you cut the target partially and your sword comes to a stop inside the target. Whatever happens in detail, you know that all or parts of the initial kinetic energy of your sword was used for creating damage since it takes energy to fracture or deform some material.

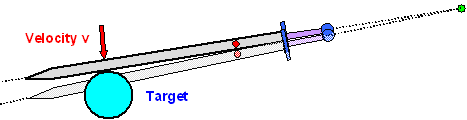
If the target is not some "body" but another sword because you need to deflect a blow of your opponent, you consider this situation:


A fully elastic collision

Your blades meet (flat side to flat side, hopefully) deform somewhat on impact, and then "bounce off" to some extent, reversing their velocity directions. You sure hope that your sword comes out undamaged of this encounter and this means that its deformation upon impact needs to be fully elastic ! Same for the sword of your opponent.

Now we have our first key topic: fully elastic collisions! If your physics teacher ever pestered you with collisions, it will have been this type. It is fairly easy to deal with - look up the science link to this topic to refresh your memory. The important insight to memorize is

Fully elastic collisions will not damage
your sword. Nor anything else

Let's move on. There is another thing you know for sure. It is shown below:


Damaging your sword

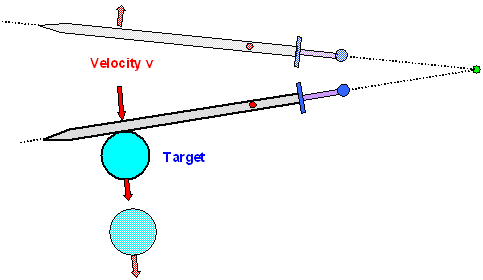
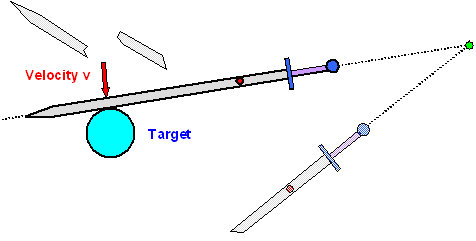
The target is heavy and hard. A big rock or an anvil, for example. If you don't own Siegfried's magical sword Notung, you are not going to do much damage to the target but you will heavily damage or fracture your sword (and possibly your wrist). It is not an elastic collision because there is damage albeit to the wrong object.

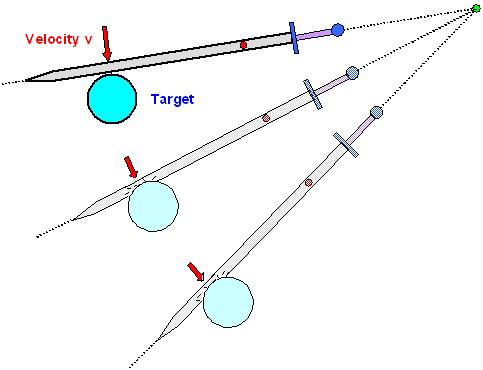
Nothing helps. If we want to optimize damage to the target, we must look at what is called an inelastic collision. The way to do that is to look first at fully inelastic collisions, the opposite of fully elastic collisions. But that would leave target and sword damaged, so in the end we need to look at the mixed case somewhere in between the extremes.
Below I show you what would happen for the classical fully inelastic collision in our scenario:


Fully inelastic collision with damage to both objects

During the collision both target and sword are inelastically, i.e. permanently deformed, then stick together and move together with some common velocity that depends on the "starting" conditions, i.e. the two masses and respective velocities.

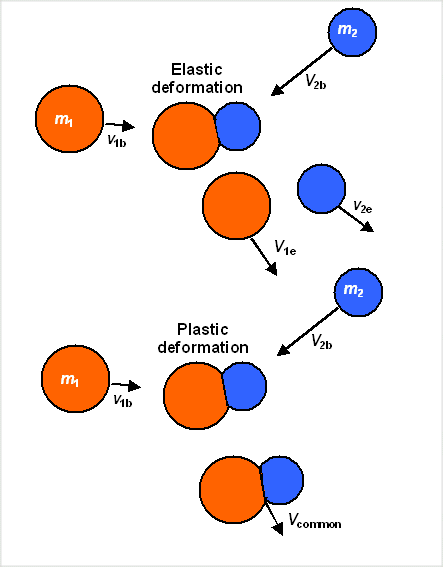
just to be on the safe side, I'll give you the two extremes - fully ellastic or inelastic collision - once more for a different kind of scenario:


The two extremes of collisions: fully elastic and fully inelastic

We are interested in the in-between case. The target should behave inelastically, allowing some damage, while our blade should behave fully elastically, not suffering any damage.

Nothing helps but going through the physics of that. It is actually not all that difficult. The conservation laws for (linear and angular) momentum and energy is pretty much all one needs. Linear momentum is linear speed times mass, angular momentum is angular velocity times moment of inertia. As far as energy is concerned, we only need to consider the kinetic energy, the energy contained in movements. It scales with mass or moment of inertia times the respective speeds squared. If we assume for simplicity a target at rest, the thing to do is:

Science Link

Collisions

Calculate the starting kinetic energy E_{kin, start} that is contained in your sword stroke.
Calculate the final velocities (both linear and angular) of sword and target after the collision.
Calculate the final kinetic energy E_{kin, final} going with these final velocities
Calculate the difference of final and stating kinetic energy, E_{kin, final} – E_{kin,
start}. That must be the energy that did damage since the total energy is conserved.

You can look up how that is done in the science module. It is quite illuminating and not all that difficult (no more than 11 equations for 11 unknowns).

The outcome is as expected.

For fully elastic collisions the total kinetic energy before and after impact is the same. Sword and target move with some velocity. There is no energy left for damage to the target.
Fully inelastic collisions provide for maximum damage energy to the target (and the sword). The damage energy delivered to the target, however, is always smaller than the total energy invested into the collision.
"In between" collision provide some damage energy to the target but always less than fully inelastic collisions.

That can best be described by invoking an "energy transfer efficiency"; a number between 0 and 1. A value of 1 would mean 100 % energy transfer, zero would mean 0 % energy transfer, and something in between, like 0,56, denotes a transfer with 56 % efficiency, i.e. at most 56 % of the initial energy is used to cause damage to the target.

Before I go into details, we must come clear about one major point. The kinetic energy in your sword stroke has to do with the speed of your blade and the mass of your sword. The way I have drawn the situation, the sword has some angular speed (measured by its circular frequency w or in rpm if you like that better). But at the point of impact we need to know the linear velocity v (symbolized by the red arrow in many of the pictures above) and not the angular velocity. And that speed is different for different points on the blade. The tip moves much faster than a point close to the hilt, for example. No big puzzle here: the speed v at some point at a distance d from the apparent center of rotation is just distance times circular frequency. You should be able to figure that out by yourself, otherwise use this link.
Moreover, you are not hitting the target with the full mass of your sword as long as the impact point is not at the center of mass. This needs to be taken into account. And we have already covered that, look at this picture again. It is the effective mass at the impact point that counts!

So in order to translate the "sword impacting a target collision scenario" from above to the standard "moving (spherical) object hits another moving (spherical) object" scenario, we have to "translate" as shown in the picture below


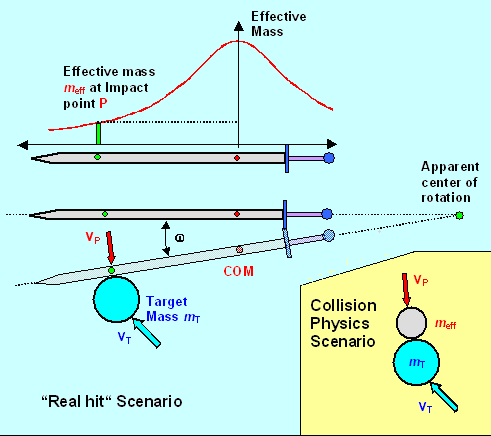"Sword hits target" scenario and how it is converted into "object hits object" scenario

For maximum impact or damage we obviously need two ingredients:

A large starting energy, translating into finding the best combination of effective mass and speed. That implies finding the best point on the blade to hit with.
A high energy transfer efficiency. That will certainly depend on target properties and possibly other parameters.

We shall look at that in the next - and last! - subchapter.