|
Angular velocity and Switching Systems |
 |
This is an Illustration and not a science link because it just illustrates your
thought processes. I'm sure that everything in here you could figure out yourself. Angela Merkel could (but possibly not
D. Trump). |
|
 |
We use the picture from the "Hitting
Something" subchapter. A sword rotates around an apparent (or instantaneous) center of rotation. How fast does
some point P somewhere on the blade move? |
| | |
|
|
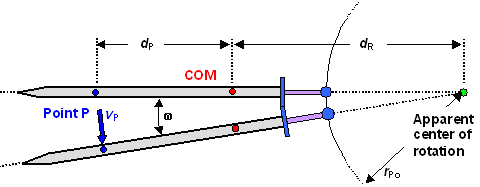 |
Movement described by a rotation around an
apparent center of rotation |
|
| |
|
 |
We assume of course a constant rotational speed or velocity. That means that the
sword will finish a full circle in some time Tcycle. It thus makes 1/Tcycle
= n full rotations per time unit. As a unit for the rotational speed you thus could give
the number of revolutions per minute and call that "rpm". You just as well could do the
number of revolutions per second and then you would call that the cycle
frequency
n with the unit "hertz" [Hz]. And yes, 1 Hz = 1/s. |
|
 |
So how fast does a point P travel that is found at some distance rP
from the apparent center of rotation? Since it travels on a perfect circle with radius r P, it
covers a distance equal to the circumference CP of a circle with radius rP
for every revolution. CP is equal to 2prP as
even D.T. might know. Since we have n rounds per second, the total distance covered in
1 second and thus the speed is 2pn · rP.
That gives us an idea: We can save a lot of writing if we don't use the cycle frequency ncycle
= 1/T cycle but something called the circular frequency (or
circle frequency) w = 2pn.
It is a simple as that. Using
w instead of n
or 1/T or, God forbid, rpm, makes writing equations much more efficient. So everybody who is anybody
uses the circular frequency and nothing else for rotational velocities. |
| |
 |
So how fast does a point P at some distance rP
from the apparent center of rotation travel? Here it is: |
| | |
|
| | |
| vP | = |
w · rP |
| | = |
w · (dP + dr)
| | | |
|
| for the point P shown |
|
|
| |
| |
 |
So far, so easy. But what happens if we do not describe the movement of the sword
as a rotation around the apparent center of rotation (COM) but, in the way discussed at length in the backbone
, as a combination of a pure translation for the center of mass plus a pure rotation around the center of mass. This is
schematically shown below. |
|
|
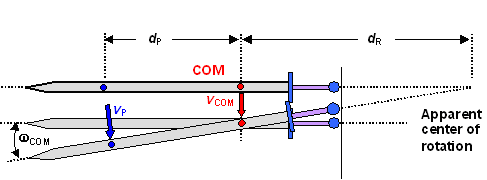 |
Movement described by a translation of, and a
rotation around the COM |
|
| | |
|
|
 |
The point P then moves with the speed of the COM which
is vCOM = w · dr plus the rotational speed for the rotation
around the COM which is vrot, COM = w COM · dP
. The circle frequency w COM for the rotation around the center of mass is
identical to the one we had before since, as the picture shows, the same rotation angle applies, i.e. w
COM = w,
This leaves us with |
| | | |
| | |
| vP | = |
wCOM · dP + w
· dr | | |
= |
w · (dP + dr) |
|
|
| |
|
| |
 |
Same as above. It also works for the kinetic energies Ekin They must
the same in both cases. With = moment of inertia for rotation around the apparent center of rotation, and ICOM
= moment of inertia for rotation around the COM, we get for the kinetic energy using the rotation around the apparent center
of rotations: |
| |
| |
| | |
| Ekin |
= ½ |
IA · w2 |
| |
= ½ |
(ICOM + mdR2)w2 |
|
|
| |
| |
| |
 |
We used the parallal
axis theorem for this; m is the mass of the sword.
Calculating the kinetic energy for the COM systen
we get |
| |
| |
| |
|
| Ekin |
= ½ |
(I COM
w2 + mv2COM) |
| | =
½ |
(ICOM + mdR2)w2 |
|
|
| |
|
 |
Just as it should be. I rest my case. |
| |
|
© H. Föll (Iron, Steel and Swords script)

