12.4.4 Impact

Energy Transfer

Below is the picture from the preceding subchapter once more. We are now considering the impact of your blade on a target with some properties:

It has a mass m_T . That might be simply its real mass. Then it might be the mass of the target plus the mass of whatever it is in close contact with. In case the target is your opponent sword, it is its effective mass at the point of impact.
The target may have a speed on its own as shown in the picture. This speed might be zero on occasion but even then we might assume that the target can be moved; at least the part that you slice off. We do not hit big rocks, anvils, or other immoveable objects any more.
The target might be rather hard (like your opponents sword) or rather soft. We already know that we can only damage targets that behave inelastically, meaning that they must be appreciably softer than your blade.


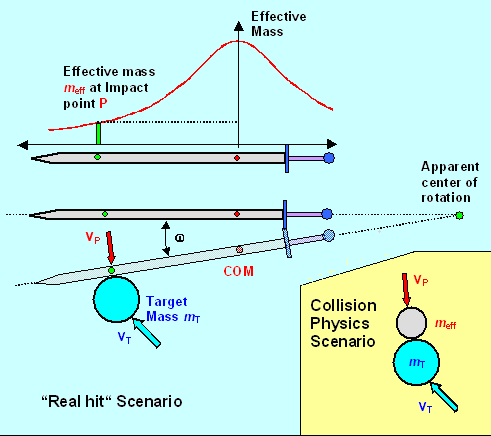"Sword hits target" scenario and how it is converted into "object hits object" scenario

We know that he damage inflicted on the target scales with

The energy contained in the blow.
The energy transfer efficiency.

Let me start with considering the last quantity first.

First of all, there is no such thing as an energy transfer efficiency in the literature about hitting things with sticks. I have made up that term. In serious collision science we would call it damage efficiency and that is indeed the term I used in the collision science module. It is easier, however, to discuss energy transfer efficiency, in particular if one is not allowed to use equations.
It is sufficient to look at simple collisions of two bodies as shown in the right hand corner above to get useful results. We assume "in-between" collisions, not 100 % inelastic but at least with a high percentage of inelasticity.
Here is what we will find for the energy transfer efficiency. First, it is a product of two components. The first one describes the degree of inelasticity of the collision, the second one the relation between the (effective) masses of sword and target.
What do we know about these quantities?

The inelasticity related energy transfer efficiency increases quickly with increasing degree of inelasticity of the target ²⁾. For a collision with only 20 % inelasticity, we still get 36 % transfer efficiency, for 30 %, 50 % or 70 % inelasticity, we get energy transfers of 61 %, 75 % and 91 %, respectively.

The mass related energy transfer efficiency increases with increasing target mass and decreasing effective blade mass. A few examples are shown in the table below

Mass relation Target : blade	Transfer efficiency
10 : 1	91 %
5: 1	83 %
2 : 1	67 %
1 : 1	50 %
1 : 2	33 %
1 : 5	17 %
1 : 10	9 %

That is a bit strange. Since I can't control the mass of the target, my best bet would be to use an extremely light-weight blade? Well, yes and no! For a given target mass the energy transfer efficiency for a light sword is larger than for a heavier one, indeed. But don't forget, we are talking transfer of energy here. With a very light blade you will indeed transfer more of the initial energy - there just isn't much energy to start with!
If you and your buddy buy a lottery ticket that wins 100 $, your cash transfer coefficient is 50 % and you are left with 50 $. If you and your remaining 99 buddies from your sword club buy a lottery ticket that wins 1.000.000 $, your cash transfer coefficient is only 1 % but you are left with 10.000 $.

Nevertheless, we can draw a few conclusions from the general rule, and I will just repeat what I have already pointed out in the collision science module.

You can't damage very small masses with your sword! The efficiency is essentially zero. In other words: Don't go after that mosquito with your katana. You might be able to move it around quite a bit but you cannot damage it. This joke ¹⁾ is thus quite funny but physically unsound. Wait until the mosquito sits down on a wall (moving up the target mass to near infinity; mosquito + wall + earth) before you hit it. And this applies to fly swatters as well as to swords.

Forging should be done on an heavy anvil. It is the total weigh of the anvil and the material to be forged that counts. You want to deform your iron, i.e. damage it. Use a not too heavy hammer and hit with speed.
Same thing for chopping wood with an axe.

Drive that nail into the wood with a relatively heavy hammer. You don't want to damage the nail, you just want to give it speed so it can damage the wood.

Guns work. The projectile is very light and will thus inflict damage on anything still lightweight yet much heavier than the projectile. The projectile is very light but extremely fast (up to 1000 m/s) and thus contains a lot of energy despite its tiny mass, and that leads to severe damage.

Light swords do not work for the reasons considered above. They will transfer their energy very efficiently to everything substantially heavier, but there is not much energy to transfer. Modern guns have muzzle speeds of more than 1.000 m/s and that gives even a light weight bullet plenty of energy. You can't get close to that speed with your sword ( 50 m/s tip velocity is already as high as it will get). And remember that speed counts quadratically.

Putting things together we have, for example a mass related transfer efficiency of 0.91 or 91 %, and an inelasticity related transfer efficiency of 0.75 or 75 %. That gives us a total transfer effciency of 0.91 · 0.75 = 0.68 or 68 %.
In other words: you will not easily get close to 100 %!

But relax. The simple collision theory employed does not account for a lot of things. First, your sword doesn't do all the fighting by itself but with you attached. That changes masses and might increase the efficiency if you use your body mass wisely.
Second, whenever your sword gets "stuck" in a partially cut target, your transfer efficiency will be close to 100 %. You can only get stuck in a heavy body, and in this case it is an almost fully inelastic collision even so your blade gets not damaged.

Blade Energy

The stating point here is the simple truth that the energy of that part of your blade that impacts the target is given by one-half of the effective mass at that point times the square of that point's velocity. The big question now is:

Which point on the blade has the
highest energy?

This is a rather tricky situation for two reasons:

The answer is not obvious.
If I move out towards the tip, the velocity increases but the effective mass decreases. Where does the product of effective mass times velocity squared peak?
We want to hit the target with that point, obviously. But we already have two other points we want to hit the target with: the percussion point and the vibration node point. Can we get these three points to coincide?

I don't know the answer to the last questions but I tend to believe that is is either not possible or only with severe sacrifices to other properties. Let's see why by looking at Turner's calculations for the blade energy as a function of the impact point position.

What we need to do is to select some sword with a known effective mass curve and move it. We could just rotate it with some circular frequency w around its center of mass (COM) or we move it in whatever way and describe that be a rotation with w around an apparent center of rotation. A point at position x on the blade then moves with a velocity that is simply given by w times the distance of the point to the rotation center.
Take the equations for the effective mass and multiply it with the equations for the velocity squared and you have (twice) the kinetic energy at the point x considered. The picture below shows schematically the two curves that need to be multiplied. Note in particular that the velocity squared curves are different for different center of rotations.


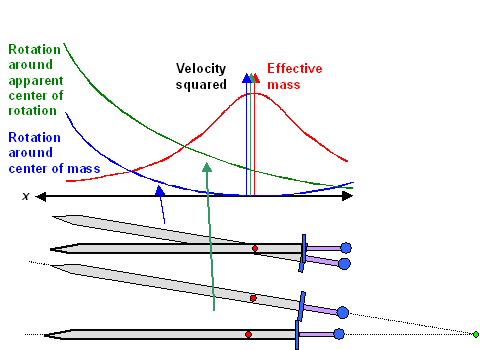Effective mass and velocity squared curves

Spelling out the equations doesn't help much because you (and even I) will not just "see" what the resulting curves will look like. Nothing helps but to wind up your computer and getting it to work. George L. Turner has done just that so I can use his results. Here is an example:


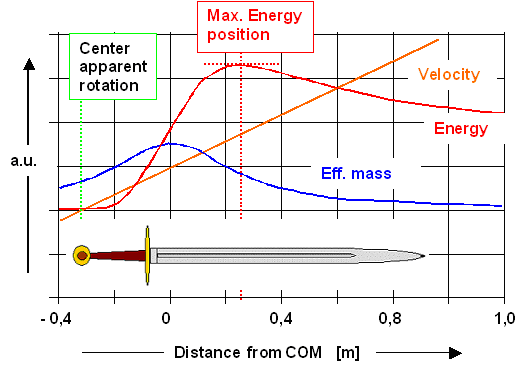Effective mass, velocity and total kinetic energy curves

Turner doesn't supply the full set of sword data so the sword inset is from me. We can deduce the apparent center of rotation because it must be at the point where the velocity is zero.

What we can see is:

The position of maximum kinetic blade energy is certainly not at "the" percussion point, the one we typically define with respect to a pivot point close to the hilt. This particular percussion point is not indicated for this sword but would be much farther down the blade for sure.
The position of maximum kinetic blade energy would certainly change for different center of rotations (the orange velocity curve would move to the left or right) . It thus cannot be at one fixed point anyway.
The position of maximum kinetic blade energy is actually located at the percussion point related to the apparent center of rotation. That is a result from Turner's book. It is, however, based on somewhat unclear math.
The position of maximum kinetic blade energy is certainly not at the position of the vibration node which is not indicated for this sword but would be much farther down the blade for sure.
The kinetic blade energy decreases from its maximum point when you go towards the tip of the blade but considerable less so than the effective mass.
Even so the tip has the highest velocity, it does not carry the highest energy.

All things considered, having the maximum energy point not coinciding with "the" percussion point and the vibration node is not so bad. In "modern" sword fights, real ones or for sports, your opponent is not heavily armored any more. If you can score a hit, it would be bad for him, even if the energy delivered is not the maximum. For thrusts the whole discussion is moot anyway. Now consider that most of your moves actually do not touch your opponent because he is deflecting your move with his sword. Half of the time you deflect his moves and that you do not with the tip area but farther down the blade - closer to where you can invest maximum energy.
What I'm saying is: Don't just look at strokes that actually damage something. Most of the time this is not what you do!

Putting Everything Together

I just told you not to focus too much on the damage energy questions. But that is exactly what I'm going to do now, just to finish this topic.
It only remains to combine the energy transfer efficiency with the blade energy. You can do that yourself following the qualitative rules given above or you could run through the math once more. Or you take it straight again form Turner's work as I'm going to do.
Tue next picture shows it all


Hitting a heavy target (KE = kinetic energy)
Source: George L. Turner

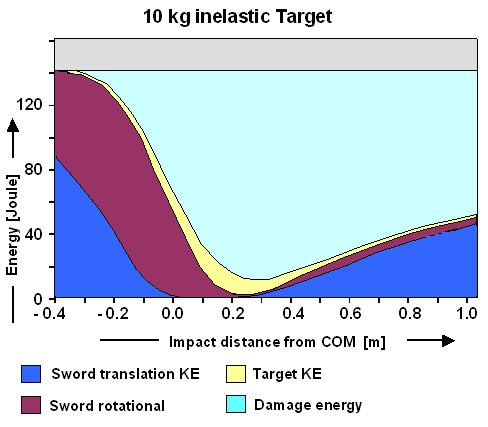
We hit an inelastic 10 kg heavy target (that can move) with a sword as shown above. You see that the maximum amount of damage energy (light blue area) is delivered about 15 cm down the blade from the center of mass, i.e. closer to the hilt than to the tip. The target is damaged by about 125 J from the total 140 J present, a 90 % all-over efficiency. If you hit with the tip (around 85 cm distance) you still deliver a little less than 100 J or about 70 %. The rest of the energy is mostly in the sword translational movement (dark blue area). The target only gets moved a little bit (yellow area).

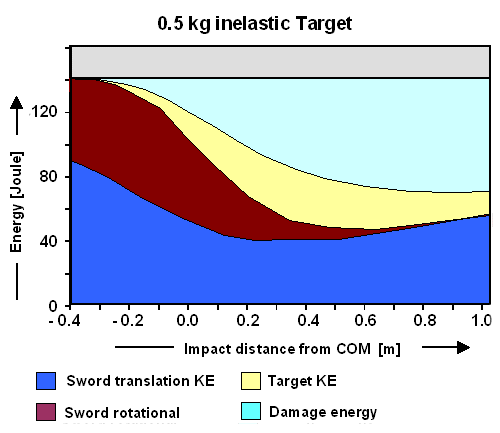
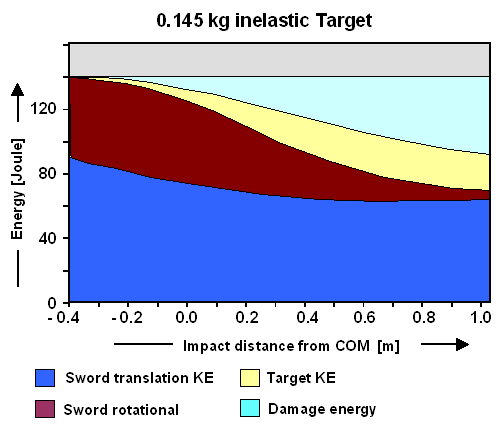
Next we look at the same general situation but with much lighter targets:



Hitting light-weight targets (KE = kinetic energy)
Source: George L. Turner

Now you deliver maximum damage energy with the tip area. In the 0,5 kg target case it is about constant for the whole tip region. However, your maximum efficiency is down to about 55 % (0,5 kg targer) or 35 % (0,145 kg target; something like a baseball). A lot of energy remains in the translational movement of the sword and also in the rotational movement. The target gets up to about 15 % of the energy just for movement, too.

The End

The End ?????

No way. This can't be the end. I can't possibly finish a hyperscript with around 480 modules and 2900 pictures by whacking you on the noggin with a sword. So read on.

¹⁾	Once the Shogun gave a reception to honor the best swordsmen in Japan. All the top samurai were in attendance along with Court nobles and beautiful geisha. A geisha approached the third highest ranked swordsmen and asked; "Sir, can you demonstrate your sword skills for me?" At once, the samurai drew his sword and cut a hovering fly in half. "Very impressive", said the geisha. When she saw the samurai who was the second highest ranked swordsmen in Japan she asked him the same question. He immediately drew his sword and with two quick strokes quartered a fly. "Most impressive", said the geisha. Then she spotted the samurai that was the highest ranked swordsmen in all of Japan. "Honorable Sir", she said "would you be so kind as to demonstrate your sword skill for me?". The samurai drew his sword and cut into the air in the direction of a nearby fly, but the fly buzzed away. "Oh, so sorry you missed", said the geisha. "But I didn't miss", said the samurai humbly "that male fly will no longer be able to have offspring."
²⁾	Using the so-called coefficient of restitution e, a number between 1 (fully elastic) and 0 (fully inelastic), that part of the energy transfer efficieny is given by 1 – e².