Collisions

General Consideration and Fully Elastic Collisions

Here I look at collisions of two bodies in some gruesome detail. It's just basic technical mechanics but that is gruesome enough for most. Much of what follows comes straight out of a text book ¹⁾ for undergraduate engineering students.
First let's see what kind of collisions we will look at in increasing order of complexity:

	1-dim. straight collision spheres / mass points
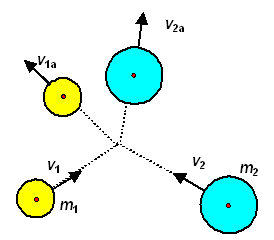	2-dim. collision spheres / mass points
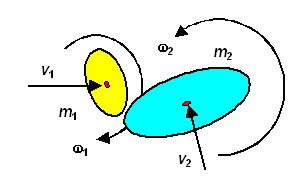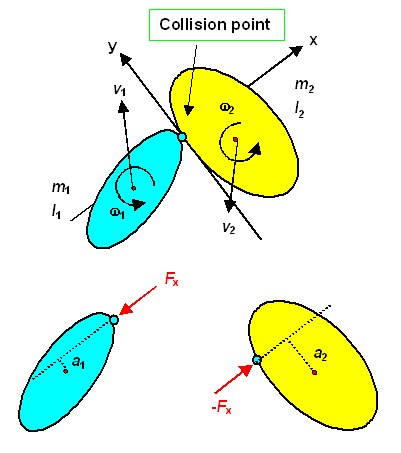
	2-dim general collision with real and rotating bodies
Kinds of collisions

To make things a bit more interesting we consider elastic or inelastic collision and anything in between.
Be happy we don't look at three-dimensional collision and only at objects with smooth surfaces (no friction when touching) and not at rough surfaces with some friction.

For starters we look at the simple first case. To add some variety, I change the situation a little bit. The yellow sphere is now chasing the blue one. Since it is obviously faster, it will eventually hit the blue one from behind. The moment just before impact is shown on the second tier.


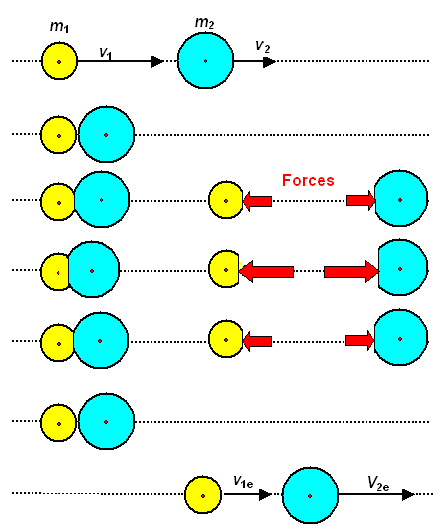Before, during, and after impact

Upon impact forces occur at t=t_begin =t_b that will accelerate the blue sphere, decelerate the yellow one, and deform elastically both of them (third tier). These forces grow to some maximun coupled to maximum deformation (fourth tier) at t=t_max=t_m . That is an interesting point in time because the two spheres are now as close together as they ever will get and move at exactly the same speed .
Think about it. There must be such at point in time and it can only be at maximum deformation. We call that "midpoint" speed v_mid
Next the de-compression or restitution stage starts. The elastic deformation is fully reversed. The spheres push each other apart with forces more or less the mirror image of what made the defamations during the compression phase. These forces will act on the masses of the spheres, changing their velocities from the common one at the "midpoint" to the final one v_1e and v_2e encountered as soon as they separate again at t =t_end=t_e.
This is shown with some (schematic) force over time diagram below:


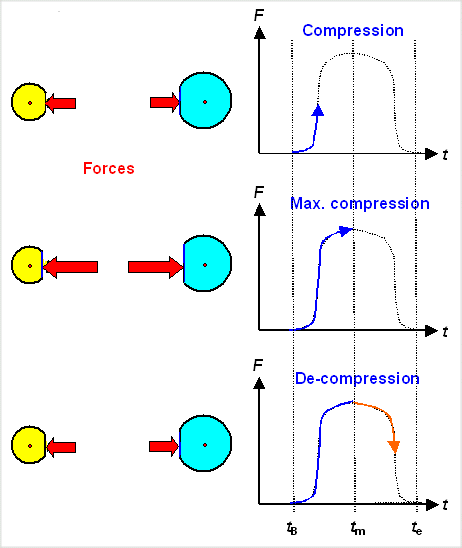Forces and deformations during the (very short) impact phase

From this consideration it is now easy to calculate what will happen for the perfectly elastic collision and - with one more simple thought - for the perfectly inelastic one, too. From that we also get the results for anything in between perfectly elastic or perfectly inelastic.
Firs, we notice that the integral over F(t)dt always gives the change in momentum of whatever mass it acts on for the time span of the integration. Integrating from t_b to t_m thus gives the total impact force acting through the compression phase; we call that impact force F_com

Important!!
An impact force is not a force! It has the dimension Ns (force times time) and the symbol F still used by all and sundry then carries some "accent" like a little something on top. That cannot easily be produced with simple HTML, so I won't do it.
In order to keep things easy, I just keep using the symbol F in what follows but always with some subscript like F_com

Similarly, integrating from t_m to t_e gives F_decom the impact force during de-compression.
It si clear that for fully elastic bodies, and therefore fully elastic collisions, the two impact forces must be identical
Writing this down, together with the momentum changes during compression and decompression, yields

F_com	=	F_decom

F_com =	– m₁(v_mid – v₁)		Compression phase
F_com =	+ m₂(v_mid – v₂ )		Compression phase

F_decom =	– m₁(v_1e – v_mid)		De-compression phase
F_decom =	+ m₂(v_2e – v_mid )		De-compression phase

Done. Five equations for the five unknowns v_1e. v_2e, v_mid , F_com and F_decom. Nothing to it. We obtain for the velocities (we don't care for the forces):

v_1e	=	2m₂ · v₂ + (m₁ – m₂ ) · v₁ m₁ + m₂

v _2e	=	2m₁ · v₁+ (m₂ – m₁) · v₂ m₁ + m₂

v_mid	=	m₁ · v₁ + m₂ · v₂ m₁ + m₂

Rather simple. For equal masses the speeds are interchanged. Mass 1 moves with the initial speed of mass 2 and vice verse. You also see that for the mass m₂ at rest (i.e. v₂=0) and m₁ representing your sword that is hitting mass 2, we can look at two extreme cases:

m₂ << m₁. We get v_1e=v₁ and v_2e=2v₁. You are hitting a fly and your don't even feel it, your sword just keeps moving. The fly is just sped up.
m₂ >> m₂. We get v_2e=0 and v_1e=–v₁. You are hitting a large rock. Your sword will just bounce off, reversing its original speed. The rock isn't doing anything.

We have (check it!) momentum preservation (i.e. m₁v₁ + m₂v₂=m ₁v_1e + m₂v_2e) and kinetic energy preservation (since ther are no other energies involved), i.e. ½m₁v₁² + ½m₂v₂²=½m₁v_1e² + ½m₂v_2e². That means that no damage of any kind occurred, the two objects after the impact are the same as before. Think of tennis rackets hitting tennis balls, golf clubs.... etc.. No damage to the bodies, only changes in velocities.

I'm not going to spend more time on this but move on to the more interesting case of fully inelastic and "in-between" collisions.

Inelastic and "Mixed" Collisions

This topic is actually quite easy to deal with. All that happens is that there is no force F_decom for the purely inelastic case. What happens in this case looks like this:


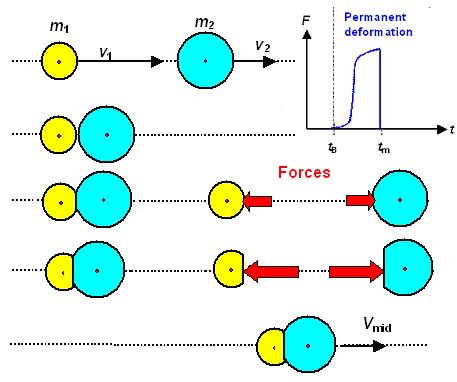Fully inelastic collision

Upon impact the two bodies deform as before but the deformation now is purely plastic, i.e. permanent. At the moment of maximum deformation, the two bodies move with the same speed v_mid and that's it! The faster yellow sphere was decelerated to v_mid, the slower one was accelerated to v_mid. Since there is no reversal of the deformation, there are no more forces after v_mid is reached (see inset in the picture above) and the two bodies now move in close contact with v_mid.
That means we can use all the equations from above if we simply omit the force F_decom , i.e. F_decom=0

What about the mixed case? Neither fully elastic nor fully inelastic? That would be the proper way to look at things if you hit a soft (rather inelastic) target with your rather elastic blade.

Well, in this case there will be a decompression phase with some force acting on both bodies. This force is, however, smaller than the force encountered during the compression phase. This changes our force equation like this

F_decom	=	e · F_com

e=coefficient of restitution; between 1 (fully elastic) and 0 (fully inelastic)

So we are still left with 5 equations for 5 unknowns, we just have one more input parameter beside the two masses and the two initial velocities: the coefficient of restitution e.

What we get for the velocities after the impact is

v_1e	=	m₁ · v₁+ m₂ · v₂–e ·(m₁ – m₂) · v₁ m₁+ m₂

v_2e	=	m₁ · v₁ + m₂ · v₂ +e ·(m₁ – m₂) · v₁ m₁ + m₂

This allows to obtain a neat little relation between the velocity difference before and after a collision. We have

v_2e – v_1e	=	e · (v₁ – v₂)

For the purely inelastic collision (e=0) we get v_2e=v_1e . The two bodies now move with the same velocity, jsut as we already deduced abive.

You can check if the preservation of momentum is still observed, i.e. if m₁v₁ + m₂v₂=m₁v_1e + m₂v_2e, and you will find that it is.
However, the total kinetic energy after the collision is no longer the same as before the collision if e < 1 obtains. This must be the case since some of the initial purely kinetic energy has beed transferred to the bodies and is no stored as "deformation" energy in the damaged bodies
This gives us a handle on calculating the damage done to the system. We define that as the energy E_dam that results from the difference of the (purely kinetic) energy E_{kin; b} before the impact and the kinetic energy E_{kin; e} after the impact, i.e.

E_dam	=	E_{kin; b} – E_{kin; e}
	=	½(m ₁v₁² + m₂v₂²) – ½(m₁v_1e² + m₂v_2e²)

E_dam	=	1 – e² 2	·	m₁ · m₂ m₁ + m₂	·	(v₁ – v₂)²

We can use this to define the damage efficiency h of a collision. It is the relation between the kinetic energy of the bodies before the collision and the Energy "used up" to produced the damage. We have

h	=	E _{kin; b} E_dam

	=	1 – e²	·	m₂ m₁ + m₂

Bingo! What the equation tells you is simple. For an efficient hit with your sword against some target with the mass m₂ you should have:

An inelastic collision, i.e. a soft inelastic target with a small e value
A target mass m₂ that is much larger than the effective mass m₁ of your blade.

Let's look at a few situations where the efficiency equation can be applied:

You can't damage very small masses with your sword! The efficiency is essentially zero. In other words: Don't go after that mosquito with your katana. You might be able to move it around quite a bit but you cannot damage it. This joke ²⁾ is thus quite funny but physically unsound. Wait until the mosquito sits down on a wall (moving up the target mass to near infinity; mosquito + wall + earth).

Forging should be done on an heavy anvil. It is the total weigh of the anvil and the material to be forged that counts. You want to deform your iron, i.e. damage it. Use a not too heavy hammer and hit with speed.

Drive that nail into the wood with a relatively heavy hammer. You don't want to damage the nail, you just want to give it speed so it can damage the wood.

Guns work. The projectile is very light and will thus inflict damage on anything still lightweight but much heavier than the projectile. It is extremely fast and thus contains a lot of energy despite its tiny mass, and that leads to severe damage.

Light swords do not work. They will transfer their energy very efficiently to everything substantially heavier, but there is not much energy to transfer. Modern guns have muzzle speeds of more than 1.000 m/s and that gives even a light weight bullet plenty of energy. You can't get close to that speed with your sword, and remember that speed counts quadratically.

Two-Dimensional Collisions

We willl just have a very a quick look at two-dimensional collisions between spheres (ensuring that we have a "central" collision). They meet at a point and we can always find a coordinate system as shown below. If the spheres have a smooth surface, meaning there is no friction, we are done.


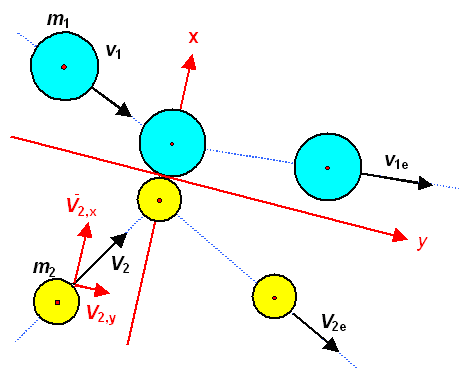Two dimensional central collision Choosing the coordinate system as shown is advantageous

We can always find a coordinate system as shown. We then look at the x and y components of the velocities (as shown for v2 separately and realize that we already have the solutions for the x components, and that nothing happens to the y components as long as there is no friction, i.e. we have spheres with "smooth" surfaces.

So just take the old solutions and add the ycomponents of the initial velocities to the final ones. No more need to be said.

Arbitrary collision

Now we look at two arbitrary bodies 1 and 2, with mass m_1,2 and moment of inertia I_1,2 (for the center of mass) with initial linear and rotational velocities like v_1,2 and w_1,2. For simplicities sakes we assume smooth surfaces, i.e. no friction.
Once more we pick a smart coordinate system with the x-axis at right angles to the (self-explaining) collision "plane". The situation then looks like this:


Close to an arbitrary collision F_x denotes the impact force

The impact force F_x follows in principle from the integration over the compressing and de-copressing real forces F_com and F_decom, related by F_decom=e · F_com as detailed above.

All we do is to write down the proper equations for the preservation of the (linear) momentum and of the angular momentum. To make things easier, we use impact forces right away and use e, the coefficient of restitution from the beginning. We obtain:

m_1x(v _1xe – v_1x)	=	– F_x
m_1y(v_1ye – v_1y)	=	0
I₁(w_1e – w)	=	+ a₁ · F_x

m_2x (v_2xe – v_2x)	=	+ F_x
m_2y(v_2ye – v_2y)	=	0
I₂(w₂ – w_2e)	=	– a₁ · F_x

The linear and angular velocities used relate to the center of mass (COM) of the two bodies. To calculate what happens upon impact, we also need the velocities v_{1,2 P} at the impact point before and after the impact. They result form the linear COM velocity plus the velocity resulting at the impact point from the rotational velocity. This is easy, we get

v_1xP	=	v _1x – a₁ · w₁		v_2xP	=	v_2x – a₂ · w₂
v_1xeP	=	v_1xe – a₁ · w_1e		v_2xeP	=	v_2xe – a₂ · w_2e

Done (almost) We have 11 equations for 11 unknowns, so get to work. We get, for example, for the total impact force F_x

F_x	=	(1 + e)	v_1x – a₁w₁ – (v_2x – a₂w₂)
F_x	=	(1 + e)	1 m₁			+	1 m₂	+	a₁² I₁	+	a₂² I₂

With that, we can write down the four after-collision speed components and the two after-collision roational velocities as

v_1xe	=	v_1x –	F_x m₁	v_2xe	=	v_1x +	F _x m₂

v_1ye	=	v_1y		v_2ye	=	v_2y

w_1e	=	w₁ +	a₁F_x I₁	w_2e	=	w₂ –	a₂F_x I₂

Another beautiful illustration of the first law of applied science! We have all the infinitely many outcomes of a tricky situation in just a few lines of equations. And we learned about the damage that can be produced (or avoided) by hitting objects with something like a sword, axe, golf club, baseball bat, ...

From here on it would be easy to move on to more complex collisions (3-dim; rough surfaces with frictions, ...) or into special "hitting" cases. Things like the percussion length would come into play but we have already looked at that in a separate module.
We could also, for example, figure out what kind of energy transfer coeffcients we have for moving and rotating objects. Let me clarify that a bit more. You can go right ahead - I will stay back, however.

¹⁾	Gros, Hauger, Schröder and Wall: Technische Mechanik 3. Springer, 9th edition.
²⁾	Once the Shogun gave a reception to honor the best swordsmen in Japan. All the top samurai were in attendance along with Court nobles and beautiful geisha. A geisha approached the third highest ranked swordsmen and asked; "Sir, can you demonstrate your sword skills for me?" At once, the samurai drew his sword and cut a hovering fly in half. "Very impressive", said the geisha. When she saw the samurai who was the second highest ranked swordsmen in Japan she asked him the same question. He immediately drew his sword and with two quick strokes quartered a fly. "Most impressive", said the geisha. Then she spotted the samurai that was the highest ranked swordsmen in all of Japan. "Honorable Sir", she said "would you be so kind as to demonstrate your sword skill for me?". The samurai drew his sword and cut into the air in the direction of a nearby fly, but the fly buzzed away. "Oh, so sorry you missed", said the geisha. "But I didn't miss", said the samurai humbly "that male fly will no longer be able to have offspring."

With frame

Percussion Point

12.4.4 Impact

12.4.3 Hitting Something