|
Percussion Point |
| |
Percussion Point Calculation for a Simple Rod |
 |
Calculating the position of the percussion point for a given pivot point is easy
for a uniform long rod and gives a good idea of what is involved.
We consider an arrangement with the geometry as shown
below. |
|
|
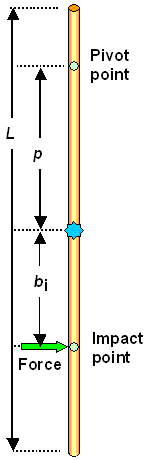 |
| Calculation of the percussion point for a rod |
|
| |
 |
We consider a rod of length L and mass m and select a pivot point at a distance p from the center of mass (which is, of course, exactly
in the middle of the rod). We strike the rod a short blow at a distance bi from the center of mass
(and, of course, on the other side of the pivot point). Note that it makes no principal difference if you apply a force
as shown (for example by hitting the rod with a hammer) or if you hit something solid with the rod rotating around the pivot
point. The rod experiences some force F. |
 |
For the velocity vCOM of the center of mass Newtons'
first law for pure translations gives us the relation |
| |
|
 |
As far as the pure rotation part is concerned, Newtons's first law is now expressed
in terms of the torque F · bi, the moment of inertia relative to the center of mass ICOM,
and the circular frequency w=2pn with n=frequency.
We obtain |
|
|
|
|
 |
For any point P at a distance p from the center of mass (and rotations),
the change of its velocity vP due to translation and rotation is given by dvP=dvCOM
– pdw. This gives us for the total change of velocity of any point P |
| |
|
dvP
dt |
= |
æ
ç
è |
1
m |
– |
p · bi
ICOM |
ö
÷
ø |
|
|
 |
If the point P is supposed to be the percussion point, it is not
supposed to move, meaning that it does not change its velocity or dvP/dt=0. This requires
that the content of the bracket in the equation above must be zero. The distance bp from the center
of mass to the special point P is the only variable or unknown in that equation and for that special distance we obtain
|
| |
|
|
| |
| |
 |
Note that reversing the situation by putting the pivot point at the location of
the percussion point and vice verse doesn't change anything on the calculation. Which name you assign to one of these points
is thus arbitrary. It is of course natural, to call the point around which real things rotate in real life the pivot point.
The other point is then automatically the percussion point, experiencing the impact force |
| |
First Consequences and Examples |
 |
That was rather painless. Let's see what it means. Take the pivot point to be
at the upper end of the rod (meaning p=L/2), recall that
the moment of inertia of a (thin!) rod for the rotation axis / pivot point shown is IRod=1/12 ·
m · L2 (neglect the component containing the rod diameter r), and you get
|
| |
|
| | |
|
| |
| |
|
 |
The percussion point, in other words, is 1/3 of the total length from the lower point of the
rod. That result is also true for a sheet (looking like the rod above if seen "on edge"). Your door is a sheet
with a defined pivot point at one end and now you know why you should put a doorstop in a place where the door hits it on
2/3 of its width. No bumping and shaking in this case. And no vibrations either because the percussion point for these simple
geometries happens to be also a node for the second vibration harmonics as shown below. |
 |
This leads over to a rather tricky issue that I will consider
in some length elsewhere. Here we only note that a percussion point
relative to some special pivot point can be identical to the position of a vibration node. But this is a special result
and not a general property. For complex geometries (like that of your sword) this is generally not
true. |
|
|
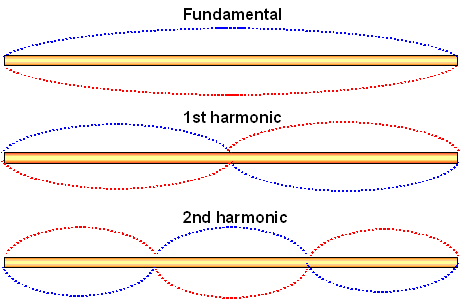 |
Vibration modes of rod (with amplitude=0
at the ends as boundary conditions)
The nodes of the second harmonic are identical to percussion
points
for pivot points at the two ends. |
|
| |
| |
| |
 |
One more thing to note about the positions of vibration nodes and percussion points is that
vibration node positions are far less sensitive to the geometry of the body in question than percussion points. They also
do not come in pairs and thus rely on the position of another point (here the pivot point) but are only determined by the
geometry of the object. If you want the vibration node and a percussion point to coincide, you should optimize the geometry
for shifting the percussion point to the desired position (e.g. by fine-tuning the pommel region) because you can assume
that whatever you do will not much affect the vibration node position. |
| | |
|
| |
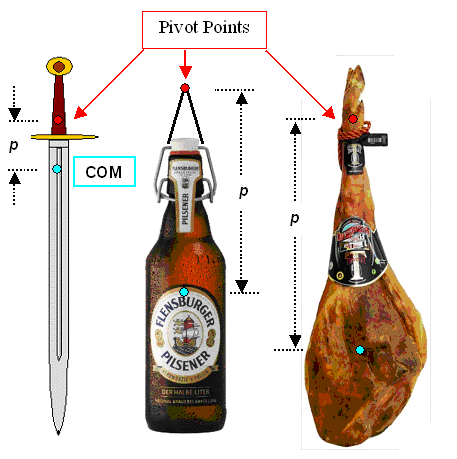
Percussion Points of Arbitrary Bodies |
 |
Replace the simple rod from above by something else, for example one of the compound
pendulums shown below. How do we find the percussion point of these things relative to some chosen pivot point? |
|
 |
Easy. The equations for the velocity change of any point on the body considered
have not changed from that of the simple rod. The result from before is thus still valid. However, all lengths were measured
from the center of mass, which is now somewhere in the body and no longer right in the middle. The moment of inertia will
also be different from that of a simple rod with the same mass as the body considered. Let's look a the picture below to
get an idea of what is involved |
| |
|
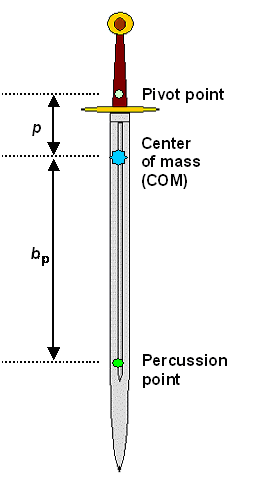 |
| | Percussion point geometry for a sword |
|
 |
Let's look at the rules concerning the percussion point that we can derive from
the equation and the picture: |
|
 |
1. The percussion point moves up / down (towards / away from the center of mass) if
the mass
m gets larger / smaller. Obvious from the equation above. But beware! Changing the mass definitely changes
the moment of inertia and that leads to the opposite effect because |
|
 |
2. The percussion point moves up / down if you decrease / increase the moment
of inertia
ICOM. That would happen, for example, if you decrease / increase the mass but in particular if
you change the mass distribution far away from the center of mass, e.g. by tapering the blade (thinner towards the tip,
broader towards the hilt) or by changing the hilt geometry, in particular the pommel mass and distance to the pivot point.
|
|
 |
3. The percussion point moves up / down if the center of mass moves down / up. Same
thing as above except that the distribution of masses counts "quadratically" for the moment of inertia and only
linearly for the center of mass. |
|
 |
4. Moving the pivot point up or down movers the percussion point up or down, too. Quite
a bit, in effect. However, this is not a good option because it should be "in" your hand so its position is rather
fixed. |
 |
Seeing that the pivot point is rather
fixed, the question is: Where do we want to place the center of mass and the percussion point? Good question! Details are
important but if we forget about them for a minute, the answer is
- Center of mass close (but not too close) to the hilt / cross guard.
- Percussion point not too far from the tip (and perhaps in the vicinity of the vibration node).
A long sword with a percussion point not close to the tip doesn't make much sense after all. |
 |
We now face a complex optimization
problem. While we can't do much about the mass (it is determined within close limits by what you can handle) or the pivot
point, the distribution of the mass determines the position of both the center of mass and the percussion point. If you
want a particular kind of blade you need top look into the fine tuning of its geometry and in particular on your hilt design.
The weight and position of the pommel might be the decisive factor for producing an optimized sword. |
| |
| |
|
The Percussion Point is the Center of Oscillation |
 |
Funny headline. What does it mean? Well, the percussion point
is also called the "Center of Oscillation" or "center of impact" for some arbitrary body. I always found that rather confusing. There seems
to be not much in common between something oscillating peacefully back and forth like the pendulum in your grandfather clock,
and something hitting something else very hard and not quite peacefully as in this
picture.
Here I will go into this step by step, starting with something that is simple and (hopefully) well known
to many readers but not closely related to swords: the mathematical pendulum. |
|
 |
We look at a "point" mass m on a "massless"
string or thin rod with a fixed pivot point some distance s from the mass.
That looks like this: |
|
|
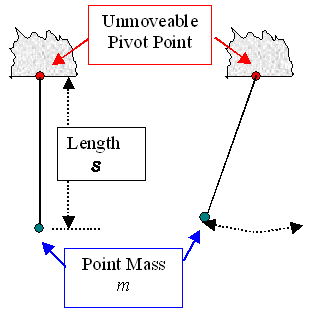 |
| Ideal point mass pendulum |
|
| |
|
|
 |
It is the classical "ideal" pendulum (or mathematical
pendulum) with an obvious moment of inertia of m · s2 for rotations around the given
pivot point. Can you find out what moment of inertia you get for the center of mass and why you get what you get? Hint 1:
The center of mass is right at the mass point. Hint 2: Use the "parallel axis theorem" ("Satz von Steiner"). Hint 3: Consider what it means to be a mathematical
point. Right. It's zero of course |
 |
Our ideal pendulum will be able to swing and it will do so in earth's gravity
(described by g=local acceleration of gravity=9.81 m/s2) with a period time or cycle
time T of |
| |
| |
| |
| T= |
2p |
æ
ç
è |
s
—
g |
ö
÷
ø |
1/2 |
| Period time of mathematical pendulum
(for small amplitudes) |
|
| |
| |
|
 |
Surprise! The mass does not enter into the equation for the cycle time T . Couldn't
be easier. Except if we use the frequency n, or better yet, the circular frequency
w=2pn=2p
/ T, something invented to make life easier for people who need to write a lot of equations. Then we have |
| |
|
|
 |
Simplicity herself. So let's get a bit more involved.We need
to look at real pendulums now, also known as compound pendulums. It is simply any
(rigid) body that is "hung" at an axis above its center of mass that is running through what is shown as pivot
point at a right angle to the screen. Something like that: |
| | |
|
| |
|
| Compound pendulums with pivot points and center of mass identified |
|
|
| |
 |
Clear enough. Now let's give them a good push so they swing back and forth and
calculate their period time T. We I find: |
| | |
|
|
|
| T= |
2p |
æ
ç
è |
lA
m · g · p |
ö
÷
ø |
1/2 |
| or |
| w= |
æ
ç
è |
m · g · p
lA |
ö
÷
ø |
1/2 |
|
|
| |
| |
| |
 |
with lA=moment of inertia relative to the
(axis through the) pivot point, m=mass, g=local acceleration of gravity and p=distance
between pivot point and center of mass. |
 |
Now that's a cool equation! First of all, it allows us a simple
experimental determination of the moment of inertia of those bodies in general and your sword
in particular. Just hang it up as shown in some way, let it swing, and measure the period time T. The moment
of inertia IA for the axis chosen, and the moment of inertia ICOM for
the center of mass then come out as: |
| | |
|
|
|
| IA |
= |
T2 · m · g · p
4p2 |
| | = |
m · g · p
w2
| | |
| |
| ICOM |
= |
IA – mp2 |
|
|
| |
| |
|
 |
The first equation comes from the one above resolved for IA, and
the second equation is just the "parallel axis
theorem" ("Satz von Steiner"). Since you know the center of mass of your sword (I showed you how to find
it easily way back here), you can easily get the distance p
between your pivot point and the center of mass, and of course you know the mass m of your sword. |
 |
Now to the next and quite important point. We consider the length
sC that the ideal or mathematical pendulum from above has to have so its period time Tideal
is identical to Tcom, the period time of our compound pendulum.
Simple. We have: |
| |
| |
| |
|
| Tcom= |
2p |
æ
ç
è |
lA
m · g · p |
ö
÷
ø |
1/2 |
= |
Tideal= |
2p |
æ
ç
è
| sC
g |
ö
÷
ø |
1/2 |
| or |
|
|
| |
| |
 |
Very simple. And very powerful because this length sC,
also known as "center of oscillation" is identical to what we just
derived for the percussion length. Now we know why there are two names for the same thing, at least as far as equations
go. But what does it mean? |
|
 |
First of all we now have a simple way to
to calculate the percussion point! Determine ICOM from the pendulum experiment, calculate
IA from that, plug in mass and the distance between pivot point and center of mass, and there you
are. |
 |
It is also clear why the name "center of oscillation" comes up. Just
realize that pivot point and percussion point are interchangeable. Take what above is identified as percussion point, make
it to a pivitö point, and your "new" percussion point is at the position of the old pivot point. And a pivot
point is by definition the "center" of an oscillation. |
| | |
|
© H. Föll (Iron, Steel and Swords script)

![]() Quantifying the Properties of Your Sword
Quantifying the Properties of Your Sword