12.3.5 Moment of Inertia

What is the Moment of Inertia?

The moment of inertia, sometimes also called angular mass or rotational inertia, is an intrinsic property of everything that has a mass and a defined body or shape. We know it's a tensor but for the time being we treat it as a number that can be used to describe a specific property of a body just like other numbers defining, for example, its mass, volume, Young's modulus, color, bra size or average income.
Bodies with the same mass can have very different moments of inertia, as they can have different volumes, colors, or sex appeal coefficients.
The following picture gives an idea of what needs to be taken into account when we determine the moment of inertia of a given body.

Consider the bodies shown below. A longish rod with a mass of 100 something (kg, g, pounds, ounces,...), various spheres at the end of a thin and essentially massless rod, always with a total mass of 100 and the center of mass right in the middle, plus a body. Guess what kind of torque it needs to make all these bodies rotate in the same way ("with equal acceleration of the rotational speed") around the axes indicated. I've indicated my guess by the length of the torque arrows.
There is no way to guess the exact length of the torque arrows but one thing is certain: It's far easier to rotate the rod around its long axis that around its center, or the one big sphere in comparison with two spheres far out on the thin rod.
The effort or torque needed to obtain a certain acceleration of the rotational speed is directly proportional to the moment of inertia. The length of the red arrows in the picture below thus also symbolize the moment of inertia of the bodies considered for the rotational axes shown.


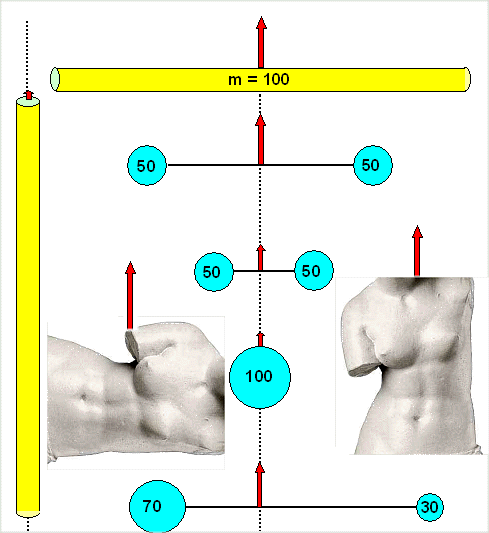Rotating bodies with equal mass but different moments of inertia The rotation axis runs through the center of mass in all examples

The picture also makes clear that one and the same body can have quite different moments of inertia. Giving only one number thus implies that you also give the rotational axis.

As a rule of thumb we can state that the distance of masses from the rotational axis is what counts for the moment of inertia. Far-out masses are more difficult to spin around than masses close to the axis. In fact, the distance from the rotation axis counts quadratically. Double it, and you need four times the effort because the moment of inertia quadruples..
Calculating the moment of inertia for any object (relative to a given axis) is easily done if you follow this simple recipe:

Divide you body into tiny cubes (think of it being made by tiny Lego blocks).
Take the mass of a cube and multiply it by the square of the distance to that particular rotational axis running through the center of mass that you have in mind.
This gives you a number with the unit kg · m². Write down that number.
Repeat the procedure for all the other blocks that you needed to produce the body.
Add up all the numbers. The result gives you the moment of inertia in units of kg · m² with respect to the axis chosen.

Science Link
Moment of inertia

Of course, if you know the least little bit about calculus, you know that the recipe above tells you to do an integral and that all of the above reduces to an equation shorter than the words "moment of inertia". How that works is shown in the science link.
However, it's far easier to measure the moment of inertia of your sword than to calculate it. How that is done I will is outlined in a science link and here.

Now let's look at the only really important point in all of that:

The moment of inertia is for
rotational movements
what the mass is for
translational movements.

When you pitch a spear, a baseball or a stone (translational movement) you "feel" essentially the mass of the object opposing the force you exert. It's more difficult to get larger masses moving.
When you rotate a gyro or your sword, it's the moment of inertia that you feel opposing the torque you apply. It's more difficult to get larger moments of inertia spinning.
Of course, the moment of inertia contains the mass of the object. But how that mass is distributed relative to the rotation axis is also part of the moment of inertia, and that is usually more important than the mass.

If you are still with me, you may have noted that we still have two major problems with respect to the moment of inertia of our swords:

There are many (in fact infinitely many) possible rotation axis one can run through the center of mass of some body. In the picture above two are shown for the rod and the body. The rotational behavior of the two cases, and thus the moment of inertia, will be quite different. We need two numbers for two axes! Three number for three axes and so on? In contrast, if we rotate a perfect sphere, all axes' are equal - only one number for the moment of inertia is needed for all possible axes!
Using my sword, I rarely rotate it around the center of mass. I rather rotate it around an axis or pivot point in the hilt (because I rotate my wrist) or an axis not even inside the sword, like an axis running through my elbow or shoulder. Generally, I can rotate it around any axis I can think of. Another infinity of possibilities and infinitely many moments of inertia?

Good questions. The answers are obvious and simple - for people with some background in physics and a knowledge of tensor algebra.
Here we go:

The moment of inertia happens to be a tensor - a collection of at most 9 "normal" numbers; but already 6 or fewer will do in our case. A tensor is a mathematical entity a bit more advanced than a vector (something needing three "normal numbers" to define it) but still rather basic stuff and just a kind of advanced number.
If you know the moment of inertia tensor for rotations around axes running through the center of mass, you can easily calculate its value for any axis. Well, maybe you can't, but I and my buddies have no problem here.

So the moment of inertia is a "number" as stated above, just not your usual or "normal" boring kind. You have encountered that before. You would give the velocity of your car as a normal number - 123 km/h for example - but on closer consideration you realize that velocity is a vector - an entity that needs three "normal" numbers to fully describe its magnitude (123 here) and the spatial direction of the movement. Typically you give the components of the velocity along the three axes of some coordinate system - three numbers!
The moment of inertia is a tensor, something a bit more complex than a vector but still in that mathematical league where "normal" numbers or scalars are known as tensors of 0th rank, vectors are of 1st rank, tensors like the moment of inertia (or stress and strain tensors) are of 2nd rank, and so on.
The moment of inertia thus is an entity uniquely associated with some body of material. We need to know it if we want to do any calculations involving rotations of the body. Young's modulus, to give another example, also turned out to be a tensor upon closer inspection. Young's modulus is actually a tensor of 4th rank, needing up to 21 "normal" numbers or scalars to fully describe it.

Working with the Moment of Inertia

Now to the good news: Not all axes of rotation are equal! You may have infinitely many axes running through the center of mass of some body but one or two immediately catch the eye if that body is not completely irregular but has some symmetry. Let's look at some examples:


Principal axes

Those special axes are called "principal axes" and - surprise - one of them will correspond to the largest possible moment of inertia the body can have, another one to the smallest, and the third one to something in between. As it turns out (after some heavy math), only rotations around principal axes are stable, and the one around the axis with the largest or smallest moment of inertia is the most stable.
If two of the three moments of inertia are identical (e.g. for cylinders or bodies shaped like an egg) only the axis with the unique value of the moment of inertia is stable.

What does "stable" mean in this context? Well, nothing whatsoever as long as we look at rotations of rigid bodies in frictionless outer space. Things change if we look at the rotation of real bodies in an environment with some (ever so small) friction.
Bodies rotating around some arbitrary axis in an environment with gravitation and some (small) friction or other disturbances (like wind blowing), will start to wobble and eventually rotate around the axis with either the largest, smallest or unique moment of inertia.
That's part of the reason why a hard-boiled egg induced to spin while lying on its side will upright itself eventually and stand on its tip. It's actually far more complicated but here is where the fun starts. Spinning objects can do very strange things!


Rotating egg standing on its tip

Thank God (or me) we don't have to delve into this. As long as the rotational speed is not very large we do not have to worry much about stable and unstable axes, centrifugal forces, and all the exciting stuff relating to "gyroscopes".

When you swing your sword, inducing a rotational movement, you swing it through a fraction of a full circle in a fraction of a second. Its rotational speed is thus around one round per second or 60 rpm. That does not qualify as large rotational speed so we forget about the complexities alluded to above.

We need to delve into one more aspect of the moment of inertial though. You now understand why your battle-axe, when you throw it, would fly like this:


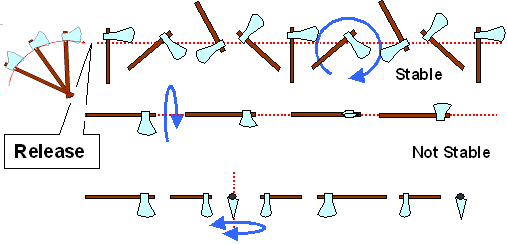Playing with an axe

On top we see a thrown axe, first rotating around a pivot point close to your fist but after release, in free flight, rotating around its center of mass. This is a stable rotation because the rotation axis is not only a principal axis but the one with the largest moment of inertia. In the second and third example the axe also rotates around principal axes but its flight is less stable. It would probably start to wobble. Of course, nobody ever throws an axe like this (how would you do it?).

The Rotation Axis Does Not run Through the Center of Mass

Finally I'm moving up to the real world! You got it by now that any movement can be de-constructed into a pure translation and a pure rotation but ther are many movements that look very much like being just a rotation and why should you describe that as a mixture? Think of a clock pendulum, your ride on a merry-go-round, the dials of your watch. We called these rotations "pivot point rotations". I will get to that in detail in then next subchapter, here I only need to point out the good news:

You can describe pivot point rotations
with the moment of inertia too!

Let's look at meaningful pivot point rotations now. Whatever we look at then rotates around a fixed axis somewhere; at a pivot point that need not be identical to the center of mass. Here are examples:


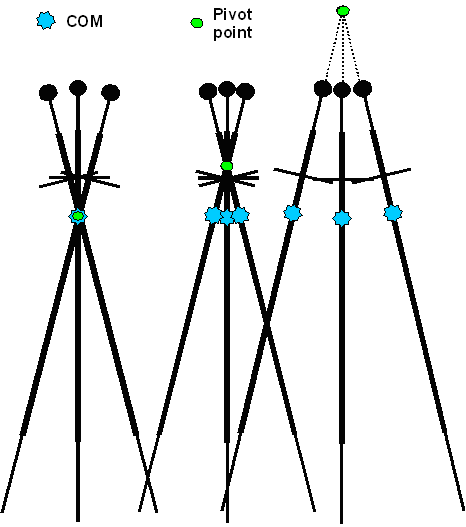Rotations around pivot points In the left case the pivot point coincides with the center of mass. In the right case the pivot point is outside the object (sword), possibly in your elbow. The middle would correspond to rotations from the wrist.

For all three cases we need a torque. You could imagine that torque to be delivered by a crankshaft perpendicular to the screen and ending on the pivot point. If you can imagine this, you just as well can imagine the torque being an arrow in crank-shaft direction, "sitting" on the pivot point with a length that is proportional to the value of the torque applied. That's just how I described a torque way up in the text.

If your muscles are somehow involved in delivering the torque, they will definitely feel an increasing resistance to a rotational movement if the distance between the center of mass and the pivot point increases. We know already that the resistance for rotations around the center of mass was given by the moment of inertia for that rotation axis. For rotations around some other axis or pivot point as shown we need to use the "parallel axis theorem" ("Satz von Steiner" in German), and that is a rather simple theorem.

It states that the moment of inertia for some axis is given by the moment of inertia for an axis running through the center of mass parallel to the axis considered, plus mass times the distance between the axes squared.
Let's look at an example: If your axes or pivot point of your 1 kg sword is 10 cm away from the center of mass, you add 1 kg · (0.1 m)²= 0.02 kgm² to the moment of inertia given for the center of mass.
You don't have to delve into this. All it means is that it gets quadratically more difficult to swing your sword or axe with increasing distance between the pivotal point of your choice and the center of mass. That already explains why it is far easier to swing a sword with a certain weight than an axe with the same weight. In the first case the center of mass is not very far from the hilt were we have the pivot point; in the second case the distance is large.

We are getting closer to being able to discuss the "handling" of elongated object like swords, axes, or golf clubs, the "feeling" you get swinging them around, and why small differences in the geometry may matter a lot. Before we do this, however, we need to delve a bit deeper into the dynamics of these objects. Partially just for fun, partially because there are still a few useful things to learn.

Illustrating the Moment of Inertia and the Parallel Axis Theorem

It is very illuminating to look at a few numbers now. Let us take an average sword with a weight or better mass of 1 kg. A bit on the light side but I'm going to use easy numbers here. The density of iron is r^iron = 7,78 g/cm³ and that demands a volume of V = 128,5 cm³. The moment of inertia then depends on how we spread out that volume and where we choose to have the rotation axis.
Below the results for three basic geometries are shown, more details can be found here. We have a simple sphere, a "blade" with two axes of rotation, and a "club" or "axe" with the whole weight at the end of a 100 cm long "weightless stick. Here are the numbers:

I_sphere	=			4 kgcm²·

I_blue	=		84,7 kgcm²
I_red	=		I_blue + 1 kg · (50 cm)² = 2 585 kgcm²

I_club	=		10 004 kgcm²

We have a variation of the moment of inertia from around 4 kgcm² to 10 000 kgcm²; an easy factor of 2 500! Remember that it is the moment of inertia that resists your efforts to swing something! The shape of your sword does matter a lot for its handling and even details may matter far more then "meets the eye".