Moment of Inertia

The Basics

Here is the recipe from the backbone for calculating the moment of inertia once more:

Divide you body into tiny cubes (think of it being made by tiny Lego blocks).
Take the mass of a cube and multiply it by the square of the distance to that particular rotational axis running through the center of mass that you have in mind.
This gives you a number with the unit kg · m². Write down that number.
Repeat the procedure for all the other blocks that you needed to produce the body.
Add up all the numbers. The result gives you the moment of inertia in units of kg · m² with respect to the axis chosen.

The crucial simplifcation is outlined in red. This being a science module, however, we will give the unsimplified version a quick look before we relax again and make life very easy.

Well, I've said it before, I say it again: The moment of inertia is actually a tensor of second rank. The defining property is the angular momentum L, the cousin of the linear momentum p=mv (m=mass, v=velocity) which happens to be an (axial) vector just like the linear momentum. You need three numbers to define it.
The mass of a body, relating the vectors of linear momentum and velocity, is a scalar, something given by just one number. There are probably very deep reasons for this. Generally, however, relating one vector to another one, calls for a tensor; I have already discussed that long ago.
The angular momentum L is given by this equation:

L_ij(x₁, x₂, x₃)=	æ ç è	L_x L_y L_z	ö ÷ ø	=	æ ç è	I_xxw_x + I_xyw_y + I _xzw_z I_yxw_x + I_yyw_y + I _yzw_z I_zxw_x + I_zyw_y + I _zzw_z	ö ÷ ø

The I_ij are the components of the moment of inertia tensor, the w_i the components of the angular velocity vector. What that means is that the angular momentum does not have to point in the same direction as the angular velocity, in contrast to the linear momentum that always points in the direction of the velocity.

As always with tensors, life becomes much simpler if one chooses a smart coordinate system. This is very easy in normal life because most rotating bodies of interest have some kind of symmetry and the "natural" axes of the coordinate system suggest themselves readily. I have covered these "principal axes" already in the backbone part. The moment of inertia tensor then reduces to

I_ij=	æ ç è	I_xx 0 0 0 I_yy 0 0 0 I_zz	ö ÷ ø

Calculating the three components is simple (in principle), provided you know the mass distribution (or, in other words, the density r (x,y,z) at every point plus the shape of the object (hidden in that innocent "V" for volume below the intergral signs that mean "integrate over the volume")

I_xx	=	ó õ	ó õ V	ó õ	r(x,y,z) · (y² + z²) dV

I_yy	=	ó õ	ó õ V	ó õ	r(x,y,z) · (z² + x²) dV

I_zz	=	ó õ	ó õ V	ó õ	r(x,y,z) · (x² + y²) dV

Well, simple in priciple, perhaps, but rather tedious in reality and practically impossible to do for shapes like a sword with a pencil on a piece of paper. There is one bonus however. When you actually go out to do the math for some common shapes, you will find that the math contains bits that look rather familiar (we hope). The equations are (mathematically) identical to those already encoutered (and possibly already done) for the area moment of Inertia. That's after all why the area moment got it's strange (and stupid) name. Noting that might safe a lot of work.

Great - but who cares? Doing those integrals today with a computer is childs play. The only problem is to get the data about shape and density into the system..

In the old days, however, people didn't have computers and many didn't even have grad students who adore tedious work. People therefore came up with some imaginative concepts to avoid the calculations and some are still very illuminating and important for considering the "handling" of swords. Here we only look at some simple examples

Examples

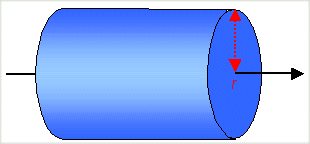
Consider a simple cylinder of some material with the mass m, the length l and a radius r . We consider the "natural rotation axis as shwon, which is, of course, a principal axis of the system. We obtain a moment of inertia as shown.
You may wonder that the equation does not contain the length l of the cylinder. It does not need to since l is already contained in the mass m. Double the length and you double the mass and thus also the moment of inertia.

I	=	m · r² 2

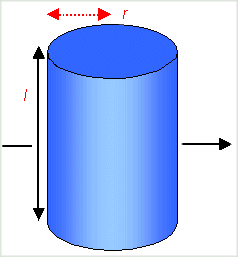
Next the same thing once more but now for a rotation around one of the other two principal axes.

I	=	m · r² 4	+	m · l² 12

Now we obviously need the length in the defining equation.
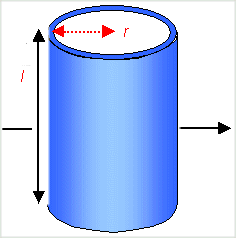
It is interesting to look at the same situation now for hollow cylinders with a wall thickness that is much smaller than the radius r. We get approximate equations that are pretty good:

I	=	m · r²

I	=	m · r² 2	+	m · l² 12

So the the moments of inertia for a full-bodied and a hollow cylinder are abut the same since the equations are not that different? Quite wrong. Consider that in order to have the same mass in both cases the radius for the hollow cylinder needs to be much, much larger.

What we see is very simply that the moment of inertia for one and same mass is much larger if the mass is "spread out". Exactly how the mass is spread out matters to some extent and makes the computations difficult, but the general trend is clear: large spreads in space cause large moments of inertia.

This gives us an idea. For any given body we can define a kind of characteristic "length of mass spreading k" by equating its actual moment of inertia (relative to some principal axis) by

I_body	=	m · k²

k	=	(I_body/m)^½

For compact bodies k would be small, for spread out ones it becomes large. People call this characteristic length k the gyration length of the body. It is one number (with the unit meter m) that characterizes the body (with respect to the chosen axis). It is not very important in the context of sword dynamics and I only introduce it to make one major point:

Don't confuse the gyration length k
with the the percussion length

The percussion length is the distance between a chosen pivot point and the percussion point. I deal with the percussion point (and other important points on your sword) in the backbone and here. At this point let me just say that what you find in the literature about all these points or lengths is not wrong but usually not easy to follow. It is easy to get a bit confused, mixing up the gyration lengh with the percussion length, the percussion length with the distance between vibration nodes, and so on.

Possible Moments of Inertia for 1 kg of Iron

A typical sword has a mass m of around 1000 g=1 kg. Let's see what we can do with that mass by distributing it in different ways. The density of iron is r^iron=7,78 g/cm³ and that demands a volume of V=128,5 cm³.

First let's look at a sphere with a weight of 1 kg. It's radius then is 3.12 cm; roughly the size of a large egg. A sphere is not what you would have in mind for a sword but it serves to give the absolute minimum of the moment of inertia one could have (around any axis going through the center, of course).
Below is how you get the numbers.

V = 128,5 cm³	=			4/3p · r³
r	=			3,12 cm
I_sphere	=			2/5 · m · r³=4 kgcm²

I_{1kg sphere}=4 kgcm²

Next we go for a very simple sword. Just a rectangular blade, 100 cm long, 4 cm wide and then by necessity 0,32 cm thick. We first look at a rotation through the center of mass, which is, of course, right in the middle.

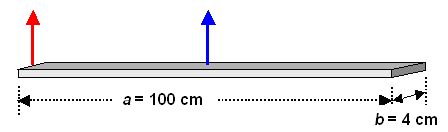I_blue	=		1/12 · m · (a² ·+ b²)
I_blue	=		84,7 kgcm²
I_red	=		I_blue + 1 kg · (50 cm)²=2 585 kgcm²

If we want the moment of inertia for an axis sitting at the end of the blade (red axis), we use the parallel axis theorem. That means we have to add mass times distance of the axes squared and obtain I_red=84,7 kgcm² + 1kg · (50 cm)² =2 585 kgcm².

Last, let's consider an axe or a club where the sphere is mounted on a "massless" rod 1 m in length with the pivot point at the end of that rod. Once more we use the parallel axes theorem and add mass times distance squared to the result for the sphere. We obtain I_Club=4 kgcm² + (100²cm² · 1 kg)=10 004 kg · cm².

I_club	=		I_Sphere + 1 kg · (100 cm)²
I _club	=		10 004 kg · cm²

We have a variation of the moment of inertia from around 4 kgcm² to 10 000 kgcm²; an easy factor of 2 500! No more needs to be said.

With frame

Quantifying the Properties of Your Sword

Science of Uniaxial Deformation

Area Moment of Inertia

Science of Deformation

Percussion Point

12.3.7 Percussion Point

12.3.5 Moment of Inertia

Collisions

Effective Mass