Effective Mass
	In order to calculate the effective mass of a sword (or any other object), we imagine the sword once more floating in outer space with a force F acting on it (for a short time). We know that the force induces a translational and rotational movement. We have already discussed what happens in this case when we looked a the percussion point; the picture below is just a repetition of the picture in the "percussion point" module. But here we don't ask which point on the sword does not move relative to the point of impact, but how different "points" along the length of the sword resist movement, or, to be precise, acceleration.
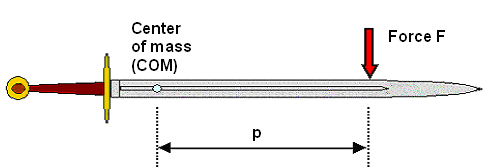		. Calculation of the effective mass of a sword
		As far as pure translational or rotational movements are concerned, we know the answer. The relation between force F or torque T and changes of the linear velocity vCOM or angular velocity w are given by the mass m or the moment of inertia I as in Newton's first law (and its extension to rotations):
		F = m · dvCOM dt     T = F · p = I · dw dt
	The total acceleration of the point p somewhere on the sword is thus the sum of the "linear" acceleration dvCOM/ dt = F/m and the acceleration caused by the rotation dvrot / dt = p · dw / dt = p · (F · p) / I = (p2 · F / I). The sum of both accelerations we may equate with the applied force F divided by the effective mass meff. We obtain
		d(vCOM + vrot) dt  =  F m  +  p2 · F I   =  : F meff meff  =   1 (1 / m) + (p2 / I)   =   m · I I + m · p2
		Done. The result is quite simple and quite amazing. It only contains the mass and the moment of inertia of the sword parameters in a kind of mixture that describes translation and rotation in one fell swoop. It does yield meff = m for p = 0 with meff decreasing symmetrically for increasing values of p. It is amazing, up to a point, because the only parameter reflecting the shape of the object besides its mass is its moment of inertia I relative to the center of mass. Plotting the result gives curves like these:
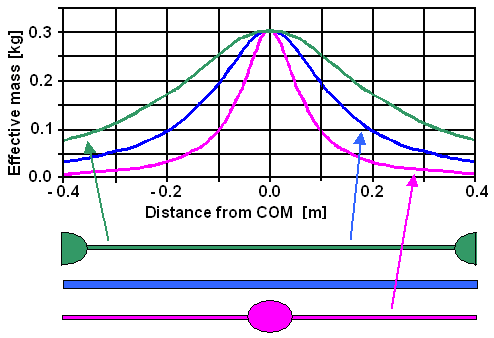		Effective mass of three rods with the same mass (0.3 kg) but different mass distributions (as schematically indicated) and thus moments of inertia I

With frame

12.4 Wielding Your Sword; 12.4.1 The Effective Mass or Apparent Inertia

© H. Föll (Iron, Steel and Swords script)