12.3.4 Rotational Movement

Rotation With Torques

Here we look at a pure rotation of some object. That means, by definition:

Its center of mass doesn't move at all. You only will observe that if there are no net forces acting on the object. Once more the emphasis is on "net".
The object must rotate around its center of mass. Otherwise the center of mass would move, something we just excluded!

That leaves only one way of introducing a pure rotation: Apply (at least) two forces, equal in magnitude but different in sign (= direction) at some distance from the center of gravity as shown schematically below. And have them act always at right angles to the objects geometric axis, i.e. the forces rotate with the object. Only then you have a constant torque in time.


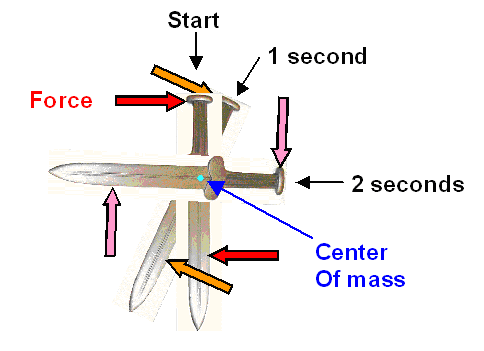Pure rotation of sword

As long as the torque is acting on the sword it will rotate around its center of mass with increasing angular velocity. Torques cause accelerations of the angular velocity just as forces cause accelerations of the "normal" velocity.
The angular velocity comes in whenever things move in a circle, it is simply how large an angle is covered in a time unit. You might cover 35^o in a second or just 6^o per second. That would make 6^o · 60 = 360^o per minute or one full circle. Then you would call it 1 round per minute or 1 rpm. Now you know.

We now must ask ourselves: how does everything depend on the forces used? Well - wrong question. Not totally wrong, of course, just a bit awkward. The better question is: How do rotational movements of arbitrary bodies depend on the torque it experiences?
Before I go into that, I will give some more consideration to the meaning of "torque ". Of course, all the nuts out there know what a torque is, and so do the bolts. You can even buy wrenches that allow to apply a pre-defined torque, like the one shown below


Applying defined torques

A torque comes up when something needs to be turned around a pivot and is simply defined as force (measured in Newton, N) times distance (measured in meter, m) between the point the force acts on and the pivot point. A torque is thus is measured in Nm - Newtonmeter; see the picture above. This is very clear to everybody who has ever tightened a nut.
Unfortunately it is also very misleading. We need to be very careful here. The familiar process of tightening a nut with a wrench like the one shown does involve a torque but it does not speed up your nut and makes it rotate faster and faster. And the sum of all forces isn't zero either - only one big force is applied, after all. It nevertheless works because there is always a lot of friction involved and because you do not just move the nut around but also your tool (not to mention parts of you), and the wrench is typically much heavier than the nut. Not to mention that the object the nut belongs to (like your car) is rather heavy and "tied down" by brakes (= lots of friction) so it doesn't move despite the force acting on it not being zero.

So sorry, but the "nuts and bolts" kind of experience with torques doesn't get us very far here. We need to look at the "ideal" situation of applying torques to objects. Ideally some object (e.g. a sword or just a long rod) in outer space (no gravity / friction) that is manipulated by massless ghosts applying forces / torques, for example as shown below:


Torques more abstract Not that this is a picture of equations, which is not the same thing as using equations!

Two forces act on our rod. They have equal strength (= equal length of the arrows) but opposite signs so their sum is zero. No net forces, no movement of the center of mass (COM).
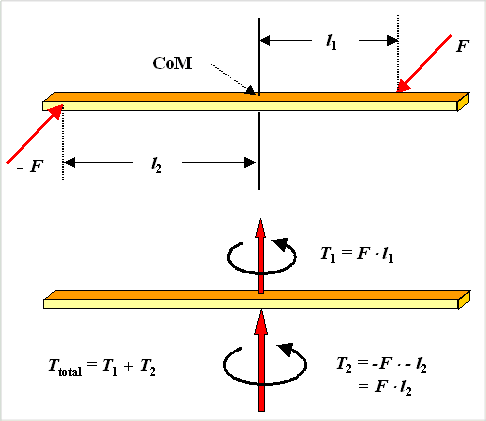
Now we will make a distinction that's a bit outside of standard physics but will help to keep the issues clear. We call the torque produced by a set of forces that add up to zero a "pure torque"
Pure torques thus can only cause pure rotations around the center of mass. Pure torques by necessity consists of two parts. We have :force F₁ times its distance l₁ to the COM (that must act as the pivot point), and F₂ times its distance l₂. The total torque is the sum of the two single ones.

Now I need to mention something rather strange, certainly not obvious: Every point on the object above feels the same torque. I show why in the picture below; skip it if you feel out of your depth, It is not important for what follows.


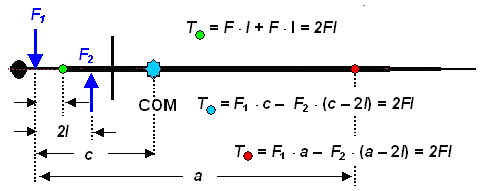A force couple with F₁ = –F₂ causing a pure torque T. Its value is the *same for any* point on the blade** !

Amazingly enough, the toque for any point is the same. Since the sword here must rotate around its center of mass (there is no net force since the forces F₁ and F₂ add up to zero) it doesn't matter in the case above where you attach the forces as long as the distance between them is the same.
All we need to know is that the presence of a torque does not automatically define the axis of rotation. In the case of pure rotations it can only be the axis through the center of mass, but for pivot rotations, the far more interesting case I will get into shortly, the rotation axis through the pivot point must be found by other means.

The pictures above give hints of how to simplify things tremendously. Since torques are for rotary movements what forces are for straight movements, it is advantageous to describe them with little arrows too. That is simple. Take the torque arrow to run along the axis of rotation and make its length proportional to the magnitude of the torque. The direction can be tied to a clockwise or a counterclockwise rotations. Doing that makes the math a lot easier (provided you have some idea about vector, or even better, tensor calculus).
We use representations like this:


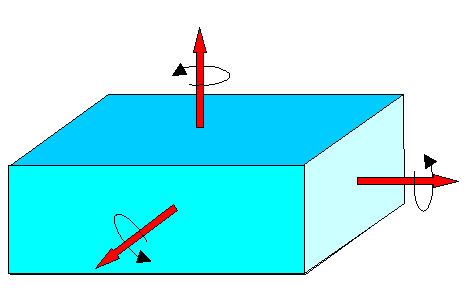Arrows parallel to the rotation axis represent possible torques. The length symbolizes the magnitude in Nm.

One more thing. The second picture above could be interpreted as showing the torque your hands impose on the hilt of your sword. Well, almost - but not quite for two reasons:

When you hold your sword at the grip you must indeed apply a torque to counter the torque felt by your wrist due to the mass of your sword. The force of gravity pulls the center of mass down and you have to counter that to keep your sword horizontal. That needs not just a torque but also a net force as we shall soon see. The sword in the picture above is obviously kept in outer space since there is no gravity. Under the conditions shown it would start to rotate.
The sword shown below does feel gravity. See if you can figure out what else it shows.
You might be able to produce forces / torques like that shown (two) above or right below for starters. The forces will make your sword move and rotate. But there is no way you can keep the torque constant for any appreciable span of time because that would mean that your hand, producing the forces, rotates with the sword.
A constant net torque is not something you or I can supply. A tricky contraption with a kind of "round sword" inside a housing, featuring magnets and coils with some current running through them might come close to applying a constant torque all the time. We would call that an electrical motor. A gasoline engine can also do this. The crankshaft of your car supplies a constant torque to the wheels and so on. But you and I can't do that.

Handling your sword (or anything else) in real life just doesn't encounter constant torques in no-friction, no-gravity environments. You rather have changing torques and forces, acting for short times only. Things in real life are just not that easy. That's why it is far more difficult to be a human than a God.


Forces while holding your sword horzontally at rest with gravity pulling downwards.

Consider what it means to just holding your sword horizontally. The pivot point would be around your forefinger / thumb and there you must add a force countering the force of gravity acting on the center of mass. But just putting your forefinger under the hilt there would keep the pivot point at rest but the sword would rotate "down". To counter that you must "push down", i.e. apply a downward force F₁ at the "other end" of your fist; above your pinky finger. How large it needs to be is easily calculated, the result is shown.
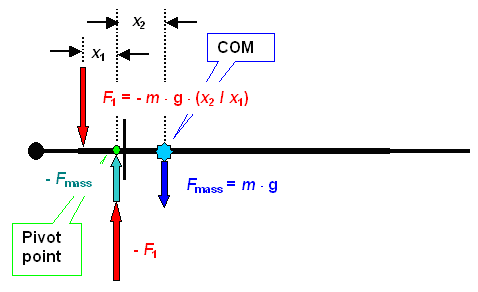
But your sword doesn't move and no movement means that there are no net forces and no net torques. Nothing helps but to add a force of magnitude - F₁ on the pivot point.
So if you want to move your sword just up and down without rotating it, you simply increase the force at the pivot point. If you want to rotate it only, you increase the force a the pivot point and with exactly the same (negative) amount at your pinky. If you want to move and rotate, ....

Don't get scared. I'm only doing the simple things here. All we need to know for pure rotational movements (no translations) is:

A pure torque acting on your sword will make it rotate around its center of mass (COM) with increasing angular velocity.
The rotation can be around any axis that runs through the COM since the torque (seen as an arrow) can have any direction.
As long as the torque acts on the sword, the rotational speed will increase (we assume no friction) or decrease if the torque is applied "the other way around" to a spinning object.
This increase / decrease or acceleration of the rotational speed is proportional to the torque and some property of the body called "moment of inertia" that takes into account the mass of the body and how it is distributed.

Yes! All of the stuff above was only to ease you into the concept of the

Moment of inertia

In short, the moment of inertia is for rotations what the mass is for translations. Since you rotate your sword far more than you translate it. As far as handling is concerned, its moment of inertia is the most important property of your sword since you usually rotate or "swing" it quite a lot.
We will need to spend some time on this. There are difficulties, however.
The moment of inertia, unlike the mass, is not just a simple number that one can attribute or assign to some given object. The best one can do for a given sword is to come up with one number relative to some rotational axis running through the center of mass. Change the rotational axis and the number changes.

Seems there are an infinity of moments of inertia for my sword - after all there are infinitely many possible rotational axes? Well - no! At most 6 numbers take care of the moments of inertia for any object. Fewer numbers are required for an object with some symmetry; for a sphere (maximum symmetry) one number would suffice.
Why is that? Well, the moment of inertia, in contrast to properties like mass or temperature, is not a "scalar", given by one number. It isn't a vector either, like the velocity, where you need three numbers (the components of the velocity for the three axes of space), worse, it is a tensor needing 9 numbers if things are really bad!

Oh f...! You certainly do not want to go this deeply into math. Well, don't worry, be happy. I'll get you there without too much pain.

Rotation Without Torques

You have applied some torque to your sword, making it rotate, but now you let it go. No more torques are acting on it. What will it do?
Same question as before for forces and translational movement. Well, the answer is much the same too.

It will keep rotating with the rotational speed it had before you let go. And no matter what kind of rotational axis was active while you "worked" your sword, it will now rotate around an axis running through the center of mass. Here is an illustration of that. Otherwise the center of mass would move, which can't be because no net forces are around in our ideal situation.
In real life your sword will fly off, rotating to be sure, and eventually fall down. That's because you cannot possibly apply a torque only with no net forces. Moreover, there is always gravity, making it fall down, and we have friction. The friction comes from the air. It's not large for a sword but it's there. Use a feather instead of a sword and you will see.
If we resort to outer space once more what will happen then is easy: You sword will keep rotating with exactly the angular momentum it had at the moment you let go. It's called:

Law of angular momentum preservation

Angular momentum is angular speed times moment of inertia and it simply gets preserved, i.e. will not change, as long as no torques are acting on the object.

No more needs to be said. You may have a beer now.
Then we proceed to a thorough discussion of the moment of inertia.