12.3.3 Translational Movement

The Problem and How to Deal with It

Let's jump right into the deep water now. We consider a sword with some force acting on it for a short time. Something like that:


Sword impacted by some (short lasting) force on some impact point somewhere.

You may see that as the situation prevailing at the precise moment when you hit something right on what I called the "impact point". To make things easy for starters, we assume that you released your grip a fraction of a seconds before impact, so your hand is not transmitting any forces on the sword at impact time. For the same reason we do this experiment in outer space, so no gravity needs to be considered.
What is going to happen?

Not so easy to tell. Partially because I was deliberately vague about what one calls the starting condition.

Is the sword just sitting there at rest with no movement whatsoever and then, suddenly, out of the blue, some forc hits it for a short time? That's what the picture implies. In this case the sword will move up ("translate") and rotate to the left (or better "counter-clockwise") around its center of mass. After the force disappears, it would keep moving and rotating at constant speed (we are in outer space, remember?).

Contrariwise, if the sword is actually swung down somehow, and the picture shows the moment of impact, the force encountered will slow down both movements, the translational and the rotational one. If the target is some unwielding large mass, the velocity of the sword will have to come down to zero since it couldn't go below the impact point. It could even reverse its movements to some extent; the sword then is "kicked back" or reflected. Maybe everything could work together in such a way that the sword just comes to a complete rest in the position shown?

Did I mention that sword movement physics is complicated? I think I did. So let's get at it systematically and slowly. Here goes:
If we look at some body moving in a way we don't know much about, we are well advised to split the movement in two parts that we then consider separately:

Pure translation of the center of mass
Pure rotation around the center of mass.

After we did that we add up the results in order to obtain the total movement. In this module we look at the translation part in some detail; rotation will be the subject of the next module.

A pure translation results from forces acting on the center of mass and nowhere else. We do not have this situation in the picture above so we need to generate it. How do we do that? By using a simple trick of physics. We "copy" the force we have and apply this (yellow) "double" to the center of mass. In order to compensate for the excess force we apply a third (blue) force that is the "mirror" image of the double also to the center of mass. The two extra forces thus cancel exactly and that's why we are allowed to do it.
Sounds a bit strange but is very powerful. Let's see why by looking at a picture of the situation


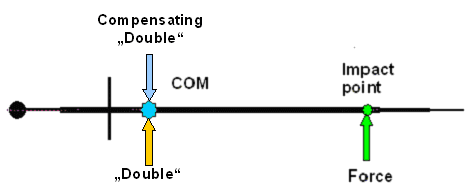Adding a (yellow) force "double" at the COM and its (blue) compensation

Things look more complicated now. So what did we gain? Quite a lot because now we can split the situation in our two cases. First we consider only what the "double" does:


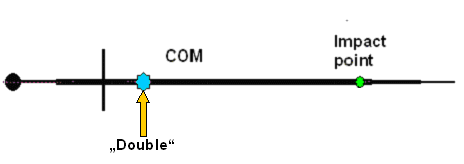*Looking at pure* translation since there is no torque and only a net force acting on the COM**

We have a force that acts right at the center of mass. It will only cause a pure translation in the direction of the force. That's what we look into here. But, for sake of completeness, let's look at what's left over:


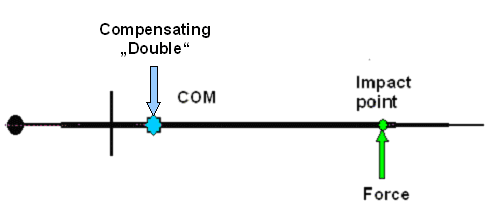*Looking at pure* rotation around the COM because there is only a torque and no net force**

Pretty cool, ain't it? We have "de-constructed" the problem into two separate problems. One deals with pure translation, the other with pure rotation. Find the two solutions and then superimpose them for the grand total.
We will do just that. In this module we look at the pure translation, in the next one we will consider the rotation.

Translational Movement

We have the case of a force acting right on the center of mass (COM). What is going to happen? Well, as you all should know, the force will move the object in its direction and, as long as it acts, it will increase the speed of the object at a constant rate or acceleration. Very basic physics tells us that. A force acting on an object causes a constant acceleration of that object that is proportional to the force and inversely proportional to its mass. This is Newton's first law, after all. You can't get more basic than that.
In other words. If, as in the picture below, we start with velocity equal to zero at the start, we have some velocity v₁ and some distance covered after 1 second, After two seconds we have doubled the velocity and quadrupled the distance. After 3 second we have three-fold velocity and 9-fold distance. And so on - as long as the force acts on the sword.


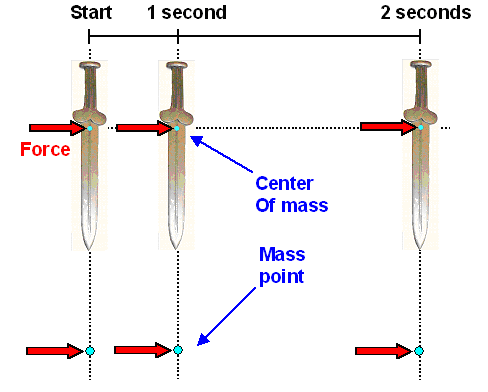Purely translational sword movement On bottom the "mass point" analogy is shown

So the force shown acts on the same point of the sword all the time! and points in the same direction all the time! . Easy to draw - but can that be? If you supply the force, you must move your arm out, or move your whole person, or do some combination. Note that it is not good enough to "keep up" with your rapidly disappearing sword but you must to keep pushing at all the time with the same force, meaning you must accelerate just as much as the sword. Obviously you can't do that for very long..
Gravity, however can do just that. Just turn the picture by 90^o to the right and you have a well-known situation: gravity pulling at your sword (and everything else):


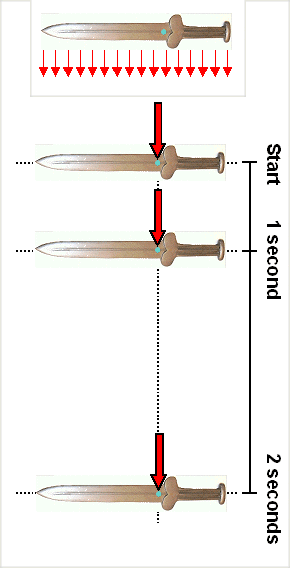Sword movement in gravity

The top part shows schematically how gravity pulls at every piece of the sword. Lots of force arrows but no torque. You can come up with as many force times distance to the COM products as you like but if you add them all up, they will always come out to zero. That is the definition of the COM, after all.
That's why we may simplify the problem by having the full "weight" pulling at the center of mass only as shown. Now we have the good old mass-point problem. Without air and therefore friction, the sword will fall with increasing velocity towards the source of the gravitation, i.e. the center of the earth until it hits a surface.
So it's actually not just a possible situation, it's a situation that is always there since you (and I) cannot switch off gravity as long as we are running around on the planet earth.
Gravity pulling at your sword (and you) is always there. What it does is relatively easy to figure out. It is, however, quite unimportant when we look at what you do with your sword. The forces encountered in sword fights, or by practicing sword fights, are far larger than the gravitational forces. You can put your blade on the neck of some delinquent for as long as you like but no head will roll because gravity pulls the blade down. You have to supply forces substantially larger than those supplied by gravity to see some action. In what follows we will therefore neglect gravitational forces most of the time.

When you use a sword (or an axe, a golf club, a tennis racket, or a hockey stick, or...) you usually hold it on one end (the hilt). Neglecting gravity, all forces acting on the sword thus concentrate on the hilt, some distance away from the center of mass. When you forcefully move your sword, these forces must be far larger than the gravitational force pulling at your sword. And yet, gravity will give a respectable speed (around 4 km/hr or 1.1 m/s) to your sword, when it accidentally falls down.
You might believe that with the much larger forces from your hand you can make your sword moving arbitrarily fast? No, you can't. All objects resist to being pushed around by forces, and some objects resist more than others.
In the universe we occupy the degree of resistance objects put up to pure translational movements depends on one object property only, that can be expressed in one simple number; the mass of the object!
Couldn't be easier! The shape, the density, the kind of material the object is made from, the weight, and so on, doesn't matter. It's the mass and only the mass that affects translational movements. Double the mass and the velocity after one second is half of what it was, the distance covered is a quarter of what it was, and so on.

Now wait a second! The weight doesn't matter? No it doesn't. It is just a measure of the force that gravity puts on a given mass close to the surface of the earth. In outer space the weight of your sword is close to zero, but its mass is the same as on earth or wherever. Its resistance to forces is the same too, even if it is weightless.

The very simple relation between force F, mass m and acceleration a has a name, by the way. It's called

Newton's First Law ¹⁾

Newton's first law states that force equals mass times acceleration or acceleration equals force divided by mass. Couldn't be simpler.
Notice once more that it's the mass and not the weight of the object we are discussing here. The weight of an object is just another word for the force it experiences in some gravity. Your weight on the moon is quite different from that on the earth (the gravity there is much smaller), your mass is the same, however.
Notice once more that I'm talking about movements by translation only. As soon as rotation comes into play, the rules change substantially!

Of course you have vague memories from high-school physics that there is something called Newton's first law, and that it somehow relates to the movement of mass points. The earth running around the sun was surely brought up, with both earth and sun imagined as points in space, imbued with some mass. Then you assumed that those two mass points interact via gravitational forces and solved the resulting differential equation for various boundary and starting conditions.
Ha ha. Very funny. You had trouble enough figuring out why the earth runs around the sun without fancy math. But even if you would go through all of the above, using up quite some space on the black board for all the lengthy equations, you still would not arrive at the well-known fact that the earth also rotates around its own axis exactly once a day. Just another reminder that we are only discussing translational movements here.

The force you can apply to your sword is larger than what gravity can do, but it is still limited. This limits the speed your sword can attain. Consider an almost massless sword. How fast can you make it move? Certainly no faster than you can move yourself running at top speed (at best around 35 km / hr). Now consider a 100 pound sword. How fast can you make it move? Right.
How fast can you make your fist move? Whatever number you come up with, your fist holding a sword cannot possibly move faster. We see a first criterion for selecting the proper mass for your sword: It should hardly slow down the velocity that your body (parts) can attain without it. That allows you to attain maximum speed before impact and to release the forces you apply just before impact since you have already obtained maximum speed. This is a smart thing to do (for example when you chop wood with an axe) because that will minimize the impact on your wrist and arms at the moment of contact.

That calls for a small mass. However, don't make the mass too small! Having a kind of long feather as a sword will allow you maximum translational speed but your opponent is not all that afraid of getting hit. Also, do not forget, that we are still talking translational, and only translational movements here. As soon as we look at rotation, more conditions for the optimal mass will appear and in the end we have to look for the best compromise.

Movement Without Forces

You have applied some force to your sword, making it move (with you attached) but now you let it go. No more forces are acting on it . What will it do?

Well, it will fly off and fall down. That's because there are still forces acting on it. One is gravity, making it fall down, the other one is friction. The friction comes from the air. It's not large for a sword but it's there. Use a feather instead of a sword and you will see.
So once more we have to resort to outer space. What will happen then is easy: The center of gravity of your sword will keep moving with exactly the velocity - magnitude and direction - it had at the moment you let go. It's called:

Law of momentum conservation

Momentum is velocity times mass and it simply gets preserved, i.e. will not change as long as no forces are acting on the object. You might recall that the energy gets preserved, too. That is correct but here momentum is the decisive property.

No more needs to be said. The momentum you imparted on your sword by the forces you supplied will be preserved until impact (forget the rather tiny contributions from gravity and friction). The thing to note is that the momentum (and the energy) will even be preserved during (and after) impact but not just for the initial single object (your sword) but the whole system (your sword, the object hit, possible attachments to the object hit, and so forth).

¹⁾	Isaac Newton: F = m · a; m = F / a; a = F / m