12.3.6 Rotational Movement

12.3.6 Translational and Rotational Movement

Grand Synthesis and the Pivot Point

I'm going to use our example from before to consider now the combination of pure translation and pure rotation for the general case. I'll just rotate the picture by 90^o to provide some diversifications. What we get is:


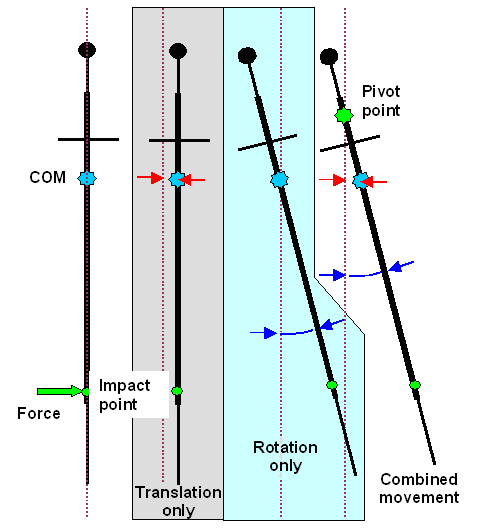Combining pure translation and pure rotation to the total movement

Clear enough (I hope). The sword moves some and rotates some around the center of mass; what you get after some short time is what you see on the right. .

What you also see is that for that particular moment in time you could just as well have described the movement as a rotation around the "pivot point" outlined in the drawing. A movement like that could be considered to be just a rotation around the pivot point. It could be achieved by only considering the torque you get by multiplying the force F by the distance t between impact point and pivot point. Graphically, with the torque shown as vector, it looks like this:


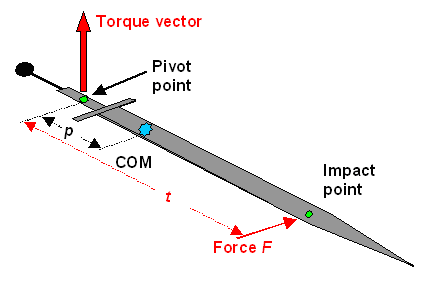Combining pure translation and pure rotation to the total movement

The moment of inertia opposing the rotation now needs to be determined by the "parallel axis theorem" and that brings us right back to the preceding sub-chapter.

This looks like a smart thing to do - we get the total movement in one fell swoop instead of going through two cases separately followed by adding them up. Well - simple pictures are often deceiving! Doing real calculations for this is not as simple as it looks in the picture because:

You don't know the position of the pivot point without calculating it first.
Here it changes with time; it is not a fixed point!

Nevertheless, the pivot point you get right after impact is of prime importance. I will devote the next sub-chapter to it (where I'm going to rename it to "percussion point").

There is, however, a simple if a bit violent way to keep the simplicity of the picture above. Nail down the system (literally!) by fixing some pivot point. Force whatever is going to rotate to do that around a fixed axis or pivot point. You then simply enforce a pivot point rotations. Look at the examples already provided to see this. Here I'm just going to repeat some of that stuff to make it stick.
Can you see that all pivot point rotations have one thing in common?

The center of mass moves in a circle!

You can produce this movement with a single torque acting on the axis, and you can calculate the rotational speeds etc. by using the relation between torque, moment of inertia for the pivot of your choice. You don't have to introduce forces, even so the center of mass actually moves. That doesn't mean there aren't forces. Your "nail" providing the pivot point might experience severe forces but as long as it holds up, you just can ignore that.
But your rotating object (and you, if you are attached to that object because it is your sword) will experience forces. You know that force, it is the centrifugal force. You will even experience the centrifugal force after you took the torque away; for zero torque. The system then rotates with constant angular speed and the center of mass also moves in its circle with constant angular speed. But that doesn't mean that its velocity is now constant. It has the same magnitude, yes, but it changes directions all the time. That counts as change of speed and thus acceleration and necessitates a force - the centrifugal force

Centrifugal forces are needed for
changing the direction of the
velocity, they don't affect the
magnitude of the velocity!

We don't have to worry much about centrifugal forces, however, because for typical sword masses and rotational speeds they are not all that large.

Apparent Center of Rotation

Going all the way back to that Samurai swinging his katana in a wide arc, we see that the center of mass does not quite move in a circle, but it is not all that far off. So it is not a simple pivot point rotation but maybe we can come up with some way to describe this movement as some other simple kind of rotation?.
Here is the picture once more:


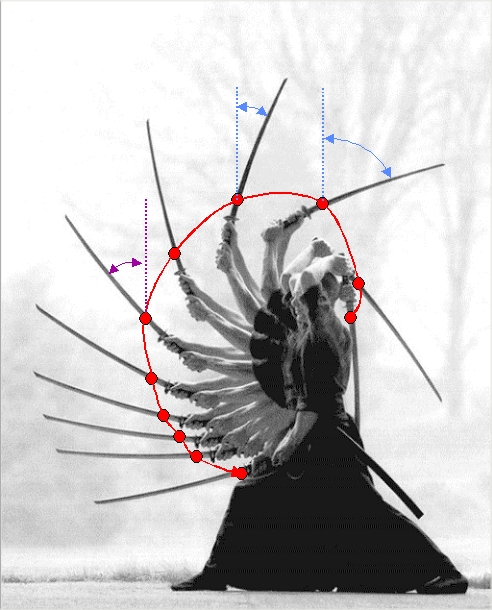The red line describes the movement of the center of mass of the sword
Source: Internet at large

What we need to do is to define the "apparent center of rotation"., also known as "instantaneous center of rotation".Easy. Draw a line through the object (here the length of the sword) at some moment in time, and repeat the procedure a short moment after. Where the two lines intersect, you have the apparent center of rotation for the point in time chosen. If we do that for the Samurai, we get the following result:


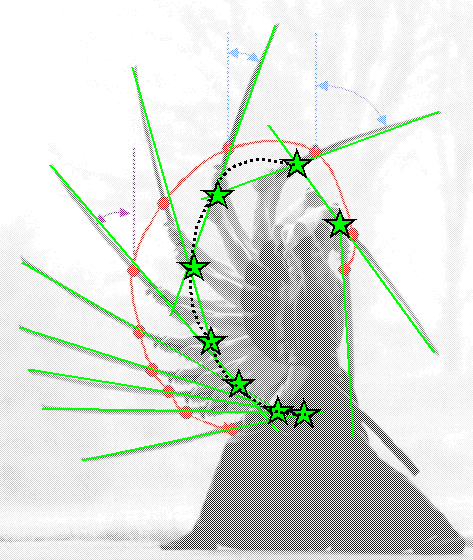Apparent center of rotation The green stars correspond to the intersection points of the green lines running through successive positions of the katana

Surprise! While it does appear that the Samurai swings his katana by rotating his arm plus katana around his shoulder, the apparent center of rotation of the katana is rather close to the wrist. What we have is a combination of rotations around three pivot points: Shoulder, elbow, and wrist.
Notice that the distance between the apparent center of rotation and the center of mass is about the same of most of the swing, meaning that the Samurai experiences about the same moment of inertia throughout.

Now you have a first glimpse into ways of analyzing sword performance. We needed to do that so we can move up to the next two important quantities: The percussion point and the effective mass of your sword.