12.2.5 Sword Types and Static Properties

Comparison of "Ideal" Swords - Bending Within the Elastic Limit

Let's perform a classical elastic bending experiment with completely different kinds of swords that are, however, completely identical in their geometry. Same blade length, same cross-section, same tapering etc. Let's look at the following list

Bronze sword
Wrought iron sword
Good ("eutectoid") steel sword
Wootz steel sword
Pattern welded sword
Japanese type sword (katana)

Let's start by assuming that all those swords are made from homogeneous and uniform materials, not containing any large defects or inclusions. In other words, we have perfect or ideal swords from a material point of view.


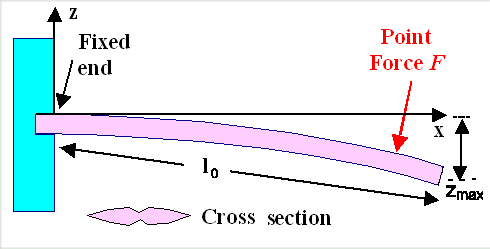Basic geometry of the bending experiment

We know that for a given force acting on the blades as shown above once more, the amount of bending or maximum deflection (given by the distance z_max) increases

linearly with the magnitude of the force. Doubling the force doubles the deflection
with the third power of the length of the blade. Doubling the length makes for 8-fold deflection
inversely linearly on Young's modulus Y. Doubling Y halves the deflection
inversely linearly on the area momentum I_A that describes the cross-sectional geometry in just one number. Doubling I_A halves the deflection

Now let's bend these swords but within the elastic limit. That means that we use forces that are not large enough to cause permanent changes in the blades. First we compare sword No 1 and No. 2:

The only difference between these swords is Young's modulus. For wrought iron and bronze we have

Y_Bronze=115 GPa
Y_{w. I.} =210 GPa

So wrought iron is considerably stiffer than bronze; about 80 % to be precise, and thus will bend about 80 % less than the bronze sword.

You should now be a bit confused since neither bronze nor wrought iron are well-defined materials. Do I mean 90% Cu / 10% Sn bronze? Arsenic bronze? Wrought iron with almost no carbon or with 0.2 % carbon? Those are different materials after all.

That is perfectly true. Nevertheless, Young's modulus for all those different copper or iron alloys, summarily addressed as bronze or wrought iron, is about the same. Differences are at most in the 10 % region and that is negligible for what we are doing here. I have emphasized that before and I have given the scientific reasons for that. In essence, Young's modulus is a property resulting from the bonding between atoms and as long as most atoms are of one kind, it is much the same. It doesn't depend much on what kinds of other atoms are mixed in as along as there are only a few percent.

Now let's include swords No. 3 - 6 in our comparison. They are made from very different kinds of steel or from several kinds in some composite construction. Nevertheless, their bending behavior in the experiment above is not noticeably different from the wrought steel sword. That's because Young's modulus of all (low-alloyed) steels is about the same for the reasons given. The large majority of bonds is still found between iron atoms.
However, in some of the steels we now may have a lot of cementite, (iron carbide, Fe₃C). Doesn't that make a difference?

Yes, it does. Young's modulus of a composite material with large percentages of other atoms will be some kind of average of the individual moduli of the constituents. I have shown you how to calculate this.
Wootz steel for example, can be seen as a composite of ferrite (=iron) and cementite (=iron carbide Fe₃ C). However, as it happens, Young's modulus of cementite, around 200 GPa, is not much different from that of iron around 210 GPa. You don't have to believe me, in reference 1 I give you one serious source plus the abstract of that paper. So no matter how you average, you end up around the value of iron.
Of course, if you look closely you will find some differences. But here we don't care about differences of 10 % or so. We simply commit to memory:

All iron / steel swords with identical
shape behave the same elastically.
Differences in elastic behavior of
iron / steel swords are always due
to differences in geometry

I know that this contradicts a large amount of what has been written about "elastic" properties of composite swords. Pattern-welded swords are almost always described as a combination of a hard but brittle steel with a soft but elastic one, giving you hard and elastic as a result. Wrong on three counts:

It's almost always a combination of a "regular" low carbon steel with a (somewhat harder, OK) phosphorous steel.
Why should the result be hard and elastic? Why not soft and brittle?
The elastic properties do not depend on what kinds of steel you combine. They are the same for each steel and any combination of steels you can conceive.

Other common mistakes often found in the literature are:

Considering that "elastic" means "not being brittle" or in other words, confusing elastic deformation with plastic deformation.
Confusing yield stress (or fracture toughness) with elasticity. A steel with a high yield stress (=hard steel) is seen as "more elastic" than a "soft" steel!

A sword might be pronounced to be more elastic for example if you can bend it to a larger degree than some other sword before something unpleasant happens.
That leads us to the second point we want to look at here: How do those still ideal swords compare if I increase the force in the bending experiment to a value where "something" happens?

	Comparison of "Ideal" Swords - Bending Beyond the Elastic Limit
	So what happens if you bend until something happens? What will happen? For the first three swords the answer is simple. All of them are ductile and therefore all of them will deform plastically as soon as their yield stress is reached. This will first take place in the outer layers as described before as soon as a critical force is reached on the bending experiment. Then the stress in the outer layers exceeds the yield stress of the material. It is not too difficult to calculate the stress in a bending experiment from the force but it is no longer straight-forward as in a tensile test experiment. If you keep increasing the force beyond the critical level, the plastic deformation spreads into the interior because deeper and deeper parts experience the yield stress. In the "neutral line (or plane) in the center, the stress is (ideally) always zero. Since yield stress is (more or less) just another word for hardness, and hardness depends not just on the chemical nature of the material but also very much on its internal structure, only general statements about the behavior of our swords can be made.
		The first general statement is easy: As soon as parts of your blade deformed plastically, it will not "snap back" to being perfectly straight after you release the force. The permanent bending effect, however, may be small for reasons considered below. Bearing this in mind, we now look cursorily at our examples form above:
	Bronze is comparable in hardness to wrought iron or even mild steel. So there shouldn't be much of difference between a bronze sword and one made from wrought iron with respect to the critical force. However, since Young's modulus of the bronze sword is smaller than that of the iron sword, it will have curved considerably more than the iron sword before it starts yielding plastically. Sword No. 3 was made from eutectoid steel, i.e. very good steel. Depending on its processing it could be harder than a bronze sword and thus could resist larger forces before plastic deformation commences. You might be able to bend it into a semicircle before "something happens", i.e. plastic deformation. The behavior of No. 4, the wootz steel sword, is not easy to predict. It should be considerably harder than a bronze sword and thus able to take a lot of force before plastic deformation starts, just like No 3. But it also could be brittle and fracture right away at some not-so-well defined stress. Pattern-welded swords as No. 5 come in many types; they are all of the composite type. If you see a pattern, there are at least two kinds of steel on the outside and the one with the lower yield stress will give first. You may not notice that, however, if the other one is rather hard, and mistake its behavior as still being fully elastic when in fact it isn't. have I have covered that before. We also may experience that "something else" happens: delamination in parts of the welds. In what follows I will look into the behavior of composite swords a bit more closely since this is important for what follows There is of course no straight double-edged katana. But we can imagine such a composite sword with a soft core and a hard outer shell like a katana; up to a point it is what's called a Viking sword. As long as the hard outer shell gives first, everything is about the same as with No 3 or 4, except that permanent bending progresses more quickly when the plastic deformation zone reaches the soft core. It gets more interesting, however, when the soft core starts to deform plastically before the hard outer shell. Think about that yourself for a while, I will get to it later.
	In the case of swords No. 4 and 5 we are looking at properties of composite swords. They are by definition "inhomogeneous" if still ideal swords. In other word, we have a composite of at least two steels with quite different behaves concerning plastic deformation and fracture, even so they have the same Young's module and thus behave identical as long as only elastic deformation is concerned. But each steel of the composite construction is still perfectly homogeneous as we assume here.
		We can't avoid any more to look a bit more closely on how an (ideal!) composite material performs in a classic tensile test or bending experiment. I will do that in the next subchapter.

¹⁾	A. P. Miodownik: "Young's modulus for carbides of 3d elements (with particular reference to Fe₃C)", Journal Materials Science and Technology Volume 10, 1994 - Issue 3; Published online: 19 Jul 2013 Absract:The Young's modulus of transition metal carbides has been calculated from their assessed thermal properties to explain why the modulus of steels and white cast irons can be only marginally altered by changes in composition or heat treatment . It is shown that the modulus of cementite (200 GN m-2) is virtually identical to the value calculated for pure ferrite (215 GN m-2). The predicted systematic variation for the modulus both with structure and position in the periodic table rationalises previous isolated experimental observations and confirms that the MC carbides of the group IV elements should have the most powerful strengthening effect in a matrix of their parent metal.