12.2. Static Sword Properties; 12.2.1 Sword Bending

12.2 Static Sword Properties

12.2.1 Sword Bending: Purely Elastic

How do parameters of your sword influence how much it bends elastically ? That necessitates to consider the basic "beam-bending" experiment as shown when I first asked this question.
Assessing static sword properties means to try to change the shape of the sword by using forces acting on it. You could, for instance, try to make it longer by pulling at it. That sounds a bit weird but that is how we assessed basic static properties of materials in chapter 3. Remember the tensile test? That gave us Young's modulus, among other things. Doing a tensile test in reverse - pushing instead of pulling - was also mentioned and we will deal with that in the next sub-chapter.

Here I look at a static load applied "sideways" or a classic bending experiment. Fix the hilt of your sword to something unmovable and then apply forces at right angles to the blade in the tip region. If we avoid immediate fracture by not using forces that are too large, the blade will bend. If we avoid permanent bending or plastic deformation by keeping the force below some limit, we will experience elastic deformation - the sword will assume its old shape again upon removing the force - and that's what we go for here.
In other words: we go for the classical "bending beam" situation. That was already discussed by Leonardo da Vinci and Galileo Galilei - but it is still the night mare of fledgling engineering students.
How you could do the experiment with an actual sword I have shown you before. Below is therefore a picture showing only the abstract essentials needed for an in-depth analys


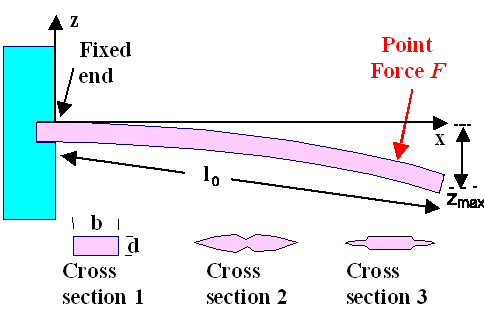Basic "bending beam" experiment. The cross-section can have any shape

Imagine that pink thing to be your sword seen sideways. What you would want to know is how much it bends for a given force. You can express the magnitude of bending - the distance indicated by the double arrow in the picture - for a given force in millimeters (or inch), so we get a number for one property of a sword now.
Measuring that number is not too difficult. But calculating that number is a daunting task. "Beam bending" is the first thing that all students have to master who are forced to attend "Technical Mechanics" lectures, and it will have been an unforgettable experience to the surviving physicists and engineers. You not only had to understand something called "area moment of inertia", you actually had to understand and be able to solve a fourth-order differential equation, requiring proficiency in differentiation and integration and a fearless mind. The links, by the way, lead you to the science modules dealing with the topic in question without avoiding equations.
This is bad news already but it will get worse! It is tough to calculate the bending of a beam with a constant cross-section but you just about can forget it completely for a variable cross-section, like for your sword. For a computer it is no problem at all, but if you try to do it with pencil and paper only, you will run into your limits rather quickly.

Now the good news: The result of rather tricky calculations is simple and easy to grasp. Let's see what we can deduce for a "sword" with a rectangular cross-section; i.e. a thickness of d and a width of b as indicated in the picture above. The thickness might be in the order of 5 mm, and the width might be around 40 mm, for example. If you apply some force - for example by putting a weight on the tip region - it will bend down a distance z_max; we may call that the deflection. What might we guess about that quantity? And what is the truth?

Guess: Double the force F and you will double z_max?
Reality: Correct as long as z_F is much smaller than the length l₀ of your blade and the force is not too large.
Guess: Double the length, and the deflection z_max will double?
Reality: Completely wrong! The deflection increases with the third power of the length! Double the length and it will be 8-fold , half it and it will be 1/8! That's why your sword will wiggle a lot more if you make it just somewhat longer.
Guess: "Stiff" materials - those with a large Young's modulus Y - will bend less than resilient materials. So the guess is that z_max goes inversely with Y?
Reality: Correct - that is what happens. Increase Y by a factor of 2 and the deflection z_max will be halfed.
Guess: A thin blade bends more than a thick one. So z_max goes inversely with the thickness d? Doubling the thickness leads to ½ of the deflection?
Reality: Completely wrong again! The deflection goes with the inverse of the third power of the thickness! Double the thickness and the deflection will be 1 / 8 of the old value.
Guess: A wide blade bends less than a narrow blade. So the deflection goes inversely with the width b of the blade?
Reality: Yes - that's correct.

Let's summarize that:

The deflection increases

linearly with the magnitude of the force. Doubling the force doubles the deflection.
with the third power of the length of the blade. Doubling the length makes for 8-fold deflection.
inversely linearly on Young's modulus Y. Doubling Y halves the deflection.
with the third power of the inverse thickness of the blade. Doubling the thickneass makes for 1/8 of deflection.
inversely linearly on the area momentum I_A that describes the cross-sectional geometry in just one number. Doubling I_A halves the deflection

Maybe you realize by now that mathematical equations are great inventions. All of the above and much more can be contained in just one line of precise symbols! The thing to remember is that the "bending property" of a sword is particularly sensitive to the length of the blade and its thickness. Or, to be more precise, to the average thickness since we never have a rectangular cross-section. If one wants to be really precise, the exact shape of the cross-section has to be taken into account by calculating its area momentum. That might be a daunting task but the result is exceedingly simple: Just one number!. The larger, the smaller the bending.
What we got so far is tricky enough - and we have not yet considered that the cross-section (and therefore the area momentum) typically changes as we go along the length of a blade. Not to mention that for curved blades we no longer have a "simple" one-dimensional problem. How do we deal with that?

Not at all - besides pointing out the obvious: The basic rules as outlined above are still valid in principle for every blade. If your sword blade tapers form hilt to tip, just conceive it as a sequence of pieces with constant but diminishing cross-sections. Each sequence bends according to the rules above, and the total shape is given by connecting the pieces. This can be seen nicely in this picture where the bending of the thin regions is more severe than in the thicker regions closer to the hilt.
If your blade is curved, it will usually not bend very much anyway since it is not very thin at any place. There is no curved equivalent of the small sword shown in the bending picture. Otherwise - see above.

What we are going to look at next is how the bending experiment and what we learned from it relates to our "classical" tensile test experiment.