12.2.2 Sword Bending: Deformation and Fracture

Bending and Relation to Tensile Testing

Heeding the first law of Materials Science, we know that in a simple bending experiment we can permanently deform or even fracture our sword. How that works becomes clear as soon as we consider what happens in a bending experiment is not really all that different from what happens a tensile test experiment. The picture below illustrates this. You may have seen it before; it was hidden in a science module way back. Now we need it in the main module but if you made it that far you will now be ready for it.


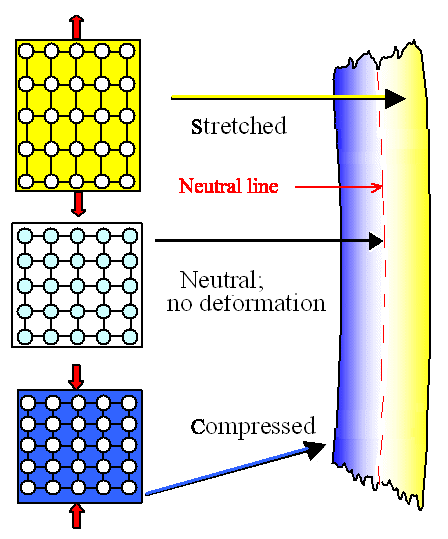Part of a bend blade

On the convex side, the material is stretched. Maximum stretching occurs at the parts farthest away from the center. Moving into the blade, the tensile stress and strain reduces and is zero at the center where we have what's called a "neutral line" (or neutral axis, neutral plane) that experiences no deformation of any kind. If we forget about secondary effects coming from things like "lateral contraction" (things pulled get longer but also get a bit thinner) we have actually a neutral plane right in the center of a symmetric straight blade
On the concave side everything is the same, just with the signs changed: Instead of tension we now have compression.

We know that ductile materials first deform elastically but switch to plastic deformation if the stress exceeds a critical value called "yield stress" or yield strength. After some plastic deformation they will eventually break.
Brittle materials do not deform plastically at all, only elastically, and break as soon as the stress is "too high". What exactly that means, and what kind of number goes with it, depends not only on the kind of brittle material in question but also very much on its internal structure, in particular the presence and size of the nano- and microcracks it contains. Refer to this module for a refresher.
The consequences of this are clear. As soon as the stress in the outer layer exceeds one of those limits, deformation or fracture will occur.

Simple! Well - not quite. The statements above are certainly true but not sufficient to describe what really happens to a real sword. There are a number of sword-related questions we now must ask:

Are the tensile stresses on one side of the blade really doing exactly the same thing as the compressive stresses on the other side?
When the bending increases, thin layers on the outside of the blade are the first to experience critical stresses. So these layers deform or break? And if they do so, does that make a noticeable difference to the blade properties at large?
Everything about critical stresses, like the yield stress and so on, always related to perfect homogeneous materials. What about real (ancient) steel, full of slag inclusions and other large particles, making it rather inhomogeneous?
Many ancient swords were composite swords, consisting of different steels with different yield stresses and so on. Some parts might even have been rather brittle. Take pattern welded blades or Japanese katanas as examples. How do these blades deform or break upon bending?
How about curved blades?

Most of the questions from above I will answer somewhat later. Here I will look at the easy ones; leading up to answering the more difficult ones later.

Getting Real

The first question is easy. What happens at some nominal stress in compression is not exactly the same as in tension . Buckling, for example, only happens for compressive stresses. Of course, the thin layer on the outside of the blade can't buckle just so; it is after all intimately connected to parts that do not want to do that. It might deform a bit differently than its stressed counterparts on the other side of the blade, however, in particular because it can do so in three dimensions .
As far as plastic deformation is concerned, there are also differences. Parts of the problem comes from the definition of the nominal stress that does not take into account that the cross-section of the sample changes when it is stressed. More to that in this link.

Nevertheless, as long as stresses are relatively small, there isn't much difference in the elastic behavior for the tensile or compressive regions (except for the change of sign, of course). As long as you only deform elastically, the differences should be minor.
Since you can bend a good blade quite a bit (once around your body if old tales are to be believed), stresses are not necessarily allways small, though. Nevertheless, as long as you deform only elastically everywhere , there isn't much difference between tensile and compressive behavior.

The key word is "everywhere". You only deform the same way everywhere if you material is perfectly homogeneous. In pronounced contrast, if your material contains microcracks or other "largish" internal defects, there is a big difference between compressive and tensile behavior. Tensile stress tends to open the cracks and thus eventually to enlargement and catastrophic sudden failure by fracture, while compression tends to close the cracks. That's why brittle materials like your toilet bowl or stone / concrete columns or walls can take lots of compressive stress but not much tensile load.
The long and short is that with increasing bending your real (old) blade, containing internal defects of all kinds, will eventually fail - by permanently deforming or by sudden fracture. Chances are that the failure starts on the tensile side.

The second question is a bit more tricky. If the outer layer experiences stresses just above the yield strength, behavior will be different from what you find in a classic tensile test. In the latter case you have essentially a one-dimensional problem. What happens somewhere in the sample happens anywhere else, too. All parts of the sample experience the same stress and react in the same way (provided the sample is perfectly homogeneous). The sample is a cylinder, a geometry with the highest possible symmetry for this case. Couldn't be easier for theoretical analysis and that's why it is the standard test.
In a bending experiment with a real sword things are far more messy. Stresses vary a lot across the sample cross-section and the geometry is tricky, to say it politely. We have a three-dimensional problem, meaning that deformation does not occur in the stress direction only.
Luckily a good computer can tell you what is going to happen for a particular sword (still made of perfectly homogeneous steel!). Provided, of course, that someone intimately acquainted with tensor math and high-level programming has produced a suitable piece of software. Forget detailed theory for a real sword made from inhomogeneous steel.

So I'm not going to dwell on this much longer but only point out one consequence. Let's assume that you did reach the yield stress for the outer layer. Then that layer will deform plastically, meaning it would stay a bit longer on the tensile side and a bit shorter on the compressive side after the stress is released. Your sword then should be permanently bend to some extent.
Well - yes, but to a smaller amount then you might expect. The reason is that next to your plastically deformed outer regions you still have a lot of only elastically deformed material in the inside. A tensed spring, in other words. This internal "spring" will exert forces on the plastically deformed parts, deforming them back to close to their original length. Your sword thus will be almost perfectly straight again - but its microstructure in the outer layers has now changed! They are elastically deformed and under internal stress. Your sword will now respond somewhat differently to the next bending experiment, and with tough luck it deteriorates from one test to the next.

Bending too hard and too often
is not a good idea!

Generalizing a bit, what I have described above is a kind of "ageing" process for a blade. It looks the same as always, but its properties have changed.

Maybe you realized that we are now already deep in question 4 from above. If your sword is a composite swords, consisting of different steels, one will yield before the other on bending or whatever stress happens to be around. Now let's turn around that question and ask: Is there any advantage of having swords made from different steels. Tough question with no easy answer.
I will look at that shortly, but for now we give question 3 some consideration: "What about real (ancient) steel, full of slag inclusions and other large particles, with carbon (and possibly phosphorous) concentration varying from one part of the blade to another?

That's easy to figure out. First, the yield stress will be different in different parts of the blade; I gave you a picture relating to this already. In an bending experiment, "weak" parts on the outside regions will thus already deform plastically while the rest is still in the elastic region. Everything said above comes into play, just in a more haphazard way.

Worse, regions with large microcracks might experience too much stress and the microcrack starts growing. In an otherwise homogeneous material evenly stressed everywhere, conditions for crack growth would lead to immediate fracture; that was the essence of fracture science, after all. In the more messy condition of an inhomogeneous material with stress gradients (because of bending), the crack growth might stop if it reaches a different kind of material or regions with stresses too low. Your blade might look the same after the bending test but at the next test it might fracture. You are testing a different material now. Its microstructure has changed after the first test, even so its outward appearance seems to be unchanged.

You also might experience sudden fracture if you bend too much - even so your material is, on average, rather ductile and should have deformed plastically first. How can that be?
Well, for sudden fracture only a relatively small part of your blade needs to be rather brittle - because of a locally high carbon concentration, a large (and brittle) slag inclusion, or something else. If a microcrack there starts growing, it might already be too large to stop at a more ductile region. It keeps going and your blade fractures totally or over most of its cross-section.

You get the drift. Real swords, especially old ones, are a far cry from being homogeneous, and that tends to make a consideration of their mechanical performance very complicated.
From what I have written so far, it appears that things always get worse if you do not have just one kind of homogeneous steel. If that would be true, their couldn't be any advantage to the production of complex pattern welded swords or any kind of "two-steel" composite swords.

Indeed, most of the time there isn't an advantage if you compare a composite sword with a sword made from just one kind of perfectly homogenous steel. However, a composite sword made from several kinds of inhomogeneous steel might still be much better than a sword made from "one" kind of inhomogeneous steel, the kind of steel humankind had to work with for most of the iron and steel history.

This is a major statement. Savor it!

Let's give question 5 a quick look. What happens when you bend a curved blade? The answer is: In principle, much of everything related above still applies. It is just a bit messier to describe in numbers since you now have always a three-dimensional problem.

What does that mean? Well, if you look at the picture above relating to a straight symmetric blade (edges on both sides), it actually shows the strain in the material. For a given distance from the neutral plane in the center of the blade, it is the same, the difference between front and back is only in the sign of the strain, and there is not much variation when you go along the blade parallel to the neutral axis either
Not so for a curved blade with an edge only on ones side and a broad back on the other. The strain and thus the stress might even vary from one side on the back to the other one. Somewhere on the blade stress are highest but where that will be depends on many things.

If you bend "too much", parts of your blade may do unpleasant things, just as the straight blade from above. In both cases it is rater unpredictable since we do not know the microstructure of the always inhomogeneous steel of old blades.

What we still need to consider is bending while pushing forward in a perfectly straight line. It's called "buckling" and we look at it in the next sub-chapter.