Bending a Sword into a Circle

Introduction

Can one bend a sword into a circle around one's body? That was instigated in the infamous "quenching a sword in a slave's body" tale and comes up in many myths of sword lore. Can one actually do this?

Well, it depends on the sword and the body. My belt needs to be more than 1 m long, so as far as my body is concerned, you need a rather long blade to achieve this feat in the first place. That's why we will only consider a semi-circle here.
I can easily bend the steel blade of a long wood saw around my body. But that "blade" is rather thin. On the other hand, I won't be able to do it with a Japanese katana or tachi because I'm not strong enough to bend these strong blades very much in the first place. So it depends very much on the thickness of the blade if the task can be done.

Let's do a little calculation to sort things out. We take a steel with the following properties:

Young's modulus of Y » 100 GPa. That is a good value for any steel.
Yield stress R_P between (0.5 - 2) GPa. Yield stresses (about the same thing as hardness) can vary a lot depending on the kind of steel used.
Length of the blade=1 m. That is on the long side but also what we need to get half around big guys.

Can you make a blade with a reasonable thickness that can be bend into a semi-circle while deforming only elastically ? That's the condition for this task, and that demands that the stress in the most challenged outer layers of the blade is still below the yield stress of the material.

Looking at the bend sword from above we get a schematic picture like this:


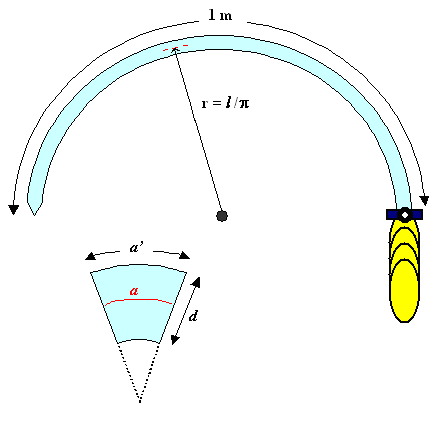Geometry of bend sword

The neutral axis is not stretched or compressed and thus still has the original length of 1 m. In the segment shown, the length of the neutral axis is just a, while on the stretched outer side it is a'. The strain e of the outer side going with this per definition is e=(a' – a)/a.
The circumference of a circle is 2pr; half of this equals the length of the blade so we have l=pr or r=l / p as noted in the figure.
For the length of the outer layer we must take a radius of r + d / 2. Putting everything together we get

e =	d 2 r	=	p · d 2 l

We stay within elastic limits as long as we do not exceed the yield stress in the outer layer. As long as we remain in the elastic region, strain e and stress s are linked by a simple relation (Hooke's law") and we obtain as condition for being able to bend the sword

s	=	Y · e < R_P

Y is Young's modulus, of course. Inserting the quantities from above we get

p · d · Y 2 l	<	R_P

d	<	2 R_P · l p · Y

That's rather cool. We have an equation that tells us how thick your 1m long blade could be for a given yield stress R_P (and Youngs modulus but that is always a given for steel swords) of the material.
Using the numbers from above (Y=100 GPa, R_P=(0.5 - 2) GPa, l=1 m) we obtain

d	<	2 · 0.5· 1 3.14 · 100	N · m · m² m² · N	=	3.18 mm

		2 · 1 3.14 · 100	N · m · m² m² · N	=	12,74 mm

Yes! We can bend a sword with a typical thickness of 5 mm - 8 mm into a semicircle if it is made from decent steel. And if our implicit assumption that the compressed side won't do anything bad is correct (it is, up to a point).
More important, however, is that we assumed that the sword was made from uniform steel that does not have weak spots, large inclusions, microcracks, or other substantial defects somewhere inside the blade. That excludes pretty much all old swords (from before 1850, say), except, maybe, wootz swords.

In other words: Old steel is never perfectly homogeneous. Old swords might nevertheless be up to the task, we just can't know without actually trying it.
Wootz swords may not contain inclusions of slag etc. but the distribution of the large amount of cementite inside the blade might not be totally uniform. They tend to be more brittle than swords from regular steel and thus might snap suddenly without much prior plastic deformation. Again, only direct testing helps.
That, however may ruin your sword because it fractures or bends permanently. Even if it doesn't and returns to its original shape, its microstructure might have changed locally. Some parts might have deformed plastically but are "pulled back" to their original shape by the surrounding material that is only elastically stretched when the stress is released. Your sword then looks the same to you - but it is not the same anymore. It is now somewhat weakened and may fracture or bend if you repeat the exercise a few times.

With frame

Sword Types

Myths and Bullshit Around Quenching

Bending of Beams

12.2.2 Sword Bending: Deformation and Fracture

12.2.5 Sword Types and Static Properties