| |
3.1.2 Stiff or Hard? |
| |
Pulling at Brittle Materials |
 |
I hope you did your homework. Now let's look at the answers
to the questions and see how well you did. |
|
 |
Let's start with the first two questions: Ponder what basic kind of stress-strain diagram you would get
while pulling at: i) a diamond rod, ii) a glass rod or any other brittle substance.
Here is what it could look like |
|
| |
| |
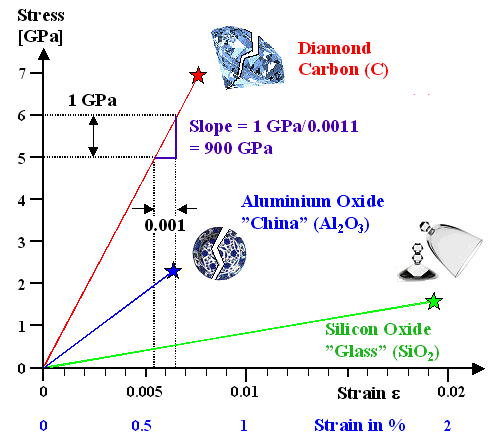 |
| Stress - strain diagrams for brittle materials
| | The "slope" part will be explained further down. |
|
| |
| |
|
 |
While my diagram shows numbers
on the axes, you didn't need to worry about that. There is no way you can know those numbers. I don't know them either but
know where to look them up (and how to cheat a little to come up with the figure). |
|
 |
What your diagram (with no numbers on the axes) should
show are at least two straight lines. A steep and long one for diamond, and a somewhat less steep and shorter one for a
glass rod or any other brittle substance. Let's see why you could have figured that
out. |
 |
If you pull at brittle materials like diamonds
or glass they will strain just a tiny bit while applying only small stress. So what - it is measurable, even if you don't
see it. If the stress is doubled, the strain doubles. If the stress exceeds some limit
called fracture stress, the material simply breaks. There is no warning in the stress
- strain curve that brittle fracture is imminent. |
|
 |
Since you probably never pulled at a glass rod you may not have experienced that first hand.
But you know that when you bend glass - or any brittle material: It breaks without warning
if you reach a small but critical deformation. Bending experiments are far more messy for calculations than just pulling
or pushing experiments but qualitatively not all that different. Double the effort and bending doubles. Too much bending
and fracture happens. So you could have guessed at some straight line for the tensile test.
There is more. If you release
the strain at any point below the fracture stress, strain and stress go right back to zero; the arrows indicate this. In
other words, the material has exactly the same length it had before the test.
We
call that kind of response to stress "elastic deformation".
All brittle
materials show only elastic behavior as longs as they don't break. |
 |
Now let's see why you could have guessed that diamond has a steeper and longer
line than other brittle materials. |
|
 |
Diamond is the hardest material out there, you know that. That can only mean that it deforms
less for equal stress than other, less hard materials. In other words, it shows less strain for the same stress then glass
or china, and thus its curve must be steeper.
Why should it be longer or going to higher stresses before it breaks?
Well - guess! What will be probably harder to break, everything else being equal? A piece of diamond or a piece of glass?
Don't tell me you would go for glass if asked this question. |
 |
My figures actually give numbers on this behavior. First of all, those numbers
show, as you suspected, that you can't elongate brittle materials much before they break. Than we have something like a
maximum stress for fracture of 7 GPa or seven Giga Pascal or 7 ·109 Pa. How much is that in everyday terms?
Well, imagine me in drag. If I borrow my wife's high heels and put all my weight on just one heel, the
stress is about 10 MPa. We need about hundred guys like me on a 1 cm2 heel, or a pin-head sized 1 mm2
heel with me alone, to produce 1 GPa.
I've already admitted that I cheated a little on two points, so now I'm going
to confess. First, materialwise, there is simply no such thing as "glass" or "china". There are many
different kinds of those materials, and they all differ somewhat in their behavior. The curves given are thus typical but
not specific. Some other glass or china specimen might show quite different curves. Nevertheless, the diamond curve is always
steeper and longer then the china curve, and so on.
Second, nobody in her right mind would do a tensile
test with brittle specimen. For
starters, they would already break when you clamp them into the machine. Moreover, even if you manage to do that with
some kind of tricks, they would fracture at values that are not characteristic for the material but just for the quality
of its surface. In real life we therefore do compressive
tests for those materials, and the numbers I used come from compressive tests, indeed. But in a thought experiment, where you don't need to worry about the boring
problems just described because you can imagine ideal surfaces and ideal clamping, the curves would come out as shown. |
 |
Now let's proceeed to the third task: Ponder what basic kind of stress -strain
diagram you would get while pulling at iii) a rubber band (let's see if you remember). |
|
 |
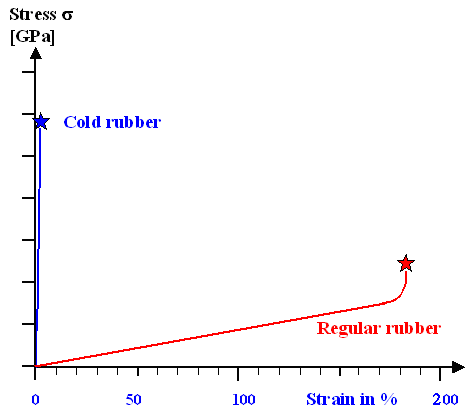
In the figure below I look at rubber once more.
Rubber at room temperature can be strained a lot and behaves always
fully elastic. Stop pulling and it always resumes its original length.
But in contrast to diamond and glass, or just
about all the "common" brittle materials, it gives you a fair warning when
it is about to break: it's stress - strain curve deviates from a straight line and goes "up". After pulling it
to a considerable length, it rather suddenly feels that it will "give" no more. That simply means that you now
have to apply far more stress to induce a bit more strain. If you ignore that warning and increase the stress, it breaks. |
| |
| |
| |
 |
| Stress - strain diagrams for brittle materials
|
|
| |
| |
 |
In the figure above I also included the stress - strain diagram you would find
at (very) low temperatures. Rubber than behaves pretty much like glass or other brittle materials. |
|
 |
I did not expect you to know that. However, you may have seen experiments where somebody puts
a rubber hose, a flower, or some other soft stuff into some liquid nitrogen and then shatters the cold things to a million
pieces by hitting them with a hammer. So what, you might have thought, the stuff now is frozen and everybody can shatter
ice with a hammer, while it's not possible with water (in bags). You're right as far as flowers are concerned but not as
far as rubber and its relatives are concerned. There is no water inside rubber that could freeze.
The "low temperature
embrittlement" of rubber led to the 1986 space shuttle "Challenger" disaster, by the way. What is going on
in inside rubber when you pull at it would be a fascinating tale on its own but since we are not overly interested in rubber
swords, I'll drop this subject right here. However, I will not drop the "low
temperature embrittlement" of steel, when I get to it! |
| | |
|
| |
Some First Conclusions |
 |
Let's describe brittle behavior in other words. Brittle materials are not given
to permanent or plastic deformation (besides
fracturing). You cannot give brittle materials a different shape by pulling or pushing at them. |
|
 |
We all know that. Nobody sober has ever tried to convert a beer glass
into a wine glass by banging it with a hammer. With a metal beer goblet, things would
be entirely different. Let's put that in large print: |
| | |
|
| | |
Brittle materials deform only elastically
and never permanently or plastically.
|
|
| |
| |
 |
Now let's generalize a bit. When you bang things with a hammer, or squeeze them
with pliers; when you pull at your hair or kick your ... (insert the target of your choice),
you are doing a deformation experiment. It's just a very unscientific experiment because you stress an irregular specimen
in an irregular way. It is nevertheless a deformation experiment. |
|
 |
Your specimen will react to whatever local stress it feels
by experiencing local strain. The kicked object will feel a lot of stress wherever it's
contacted by the tip of your boots and not much (physical) stress anywhere else. It will respond with a lot of strain at
that point and react to that by some deformation (and, if your specimen is an animated object, by making noises and kicking
back). |
 |
Let's formulate a simple but important truth: |
| |
| |
| |
Any deformation can be calculated by
considering the local
stress - strain conditions
|
|
| |
|
| |
 |
Note that I did not say "easily calculated". It is in fact a rather difficult task.
Nevertheless, if you break your diamond in a (virtual) tensile test or by banging it with a hammer, the material "diamond"
responds to the acting stress via its specific properties that describe this material. And so does your sword. |
 |
The next thing to note is that temperature must be considered, the rubber example
demonstrates that rather dramatically. On the other hand, our brittle materials from the first tasks do not change their
behavior very much with temperature. |
|
 |
All I want to do here is to make you aware that temperature might be important. Some materials
like rubber (and possible your sword) become far more brittle at low temperatures, others like glass or silicon (Si), lose
their brittleness at higher temperatures and become viscous or ductile.
This will be of major importance for what follows. |
 |
Maybe you noticed that so far I did not bring up the "strain
rate" that I used for our virtual experiments. Strange, considering that I made such
a fuss about that in the preceding subchapter. |
|
 |
Well, it turns out that for the experiments we did so far, the strain rate doesn't matter
much. We get essentially the same curves for different strain rates, just believe me on this. It is nevertheless important
that you do the experiments in a well-defined way. |
 |
Some space above I made a big deal about the length
and the slope of the straight lines describing the elastic deformation of brittle materials.
That are, of course, the two properties that distinguish different brittle materials. We sure must look at this in more detail.
|
| |
|
| |
Fracture Stress and Young's
Modulus |
 |
Let's start with the "length" of the stress - strain curve. It simply
tells you where the curve ends or, in other word, at what stress and strain the material breaks. |
|
 |
Great. Let's define a fracture stress and
a fracture strain for the material in question and tabulate it as in intrinsic and important
property of that material. Well - no, let's not! As hinted at above, fracture of real brittle
material occurs for all kinds of reasons that are not properties of the material itself.
You cannot shatter you car window glass by banging it as hard as you can with a hammer (try it). Then scratch it just a
tiny little bit with something hard like the diamonds in your ring, and it will now fracture immediately on the slightest
impact. That's why you have these little hammer in busses and trains with a very hard tip to scratch and shatter the windows
in an emergency. |
|
 |
I will have a lot to say about fracture in modules to come. Here we just note
that tensile (or compressive) tests (done right and with all kinds of tricks) will give you only a very rough idea about
the fracture properties of materials and that is why I won't go into that any more. |
 |
So let's look at the slope of the stress -strain
diagrams. As long as we have straight lines, the slope is the same everywhere and that's why we will give it a name:
|
| |
| |
| |
|
| |
| |
|
 |
How one measures a slope is shown for the diamond curve in the top figure. Draw some triangle to the curve as shown and divide the length of the vertical part by the length
of the horizontal part. As long as you do that with a straight line, it obviously doesn't matter how large the triangle
is. For diamond, a Young's modulus of 125 GPa results. |
|
 |
Young's modulus is also
called tensile modulus; or a bit sloppily elastic modulus
or modulus of elasticity. The sloppiness comes from the fact that there are several elastic moduli for a given material. Young's modulus is just one of them but the most important one.
|
|
 |
By the way, if you know the least little thing about calculus, you realize that
the definition above applies to all curves, not just straight lines. If calculus is
not something you know and enjoy, forget this remark. |
 |
The five curves in the two figures above represent substantial differences with
respect to Young's
modulus of the materials tested. For the first three curves you can derive Young's modulus yourself, for the rubber
case you can't because I didn't give numbers on the axes'. What you can appreciate, however, is that Young's modulus of
cold rubber is much larger that that of rubber proper. It can easily be more than 1000 times larger! |
 |
Young's Modulus is instrumental for the stiffness
of your blade, so we need to look at it in some detail. Let's re-express the definition from right above: |
| |
|
| |
Young's modulus measures how much stress
it takes to deform a material by 0.01 %
|
|
| |
| |
|
 |
Young's modulus thus describes a special stress
and thus is given in units of stress = force per area. It is typically given in "Gigapascals"
or GPa, meaning one billion
(= 109 = Giga) Pascals. Pascals are force (= Newton = N) per area. I covered that already but I promised repetitions. |
|
 |
Materials with a large Young's modulus take
a lot of stress to make them a bit longer, materials with a small
Young's modulus elongate easily. The same is true for bending something elastically.
As ascertained before, Young's
modulus is directly related to the slope or the steepness
of the curve in a stress - strain diagrams or their derivative in mathematical terms.
Now I have used the d-word. Since the "derivative" (of a function) is a dirty word for many, I will not go on
but refer the brave to the science module that deals with the issue.
| |
|
| |
|
The simple rule is: Steep curves relate to large Youngs' moduli, flatter curves
to smaller ones as shown in the figure above. Rubber at room temperature has an extremely small Young's modulus. |
| |
|
| |
Characterizing Materials by Their Young's Modulus |
 |
Now that we have characterized materials by their Young's's modulus,
we need a name for the property assessed in this way. What would you
call the property described by Young's modulus?
- Toughness? No! That word we have already equated with ductile
behavior.
- Hardness? Nice try! A diamond has a larger Young's modulus than glass and is harder,
indeed. So thanks - but no! Hard materials tend to have a large Young's modulus but there is no direct relations. Young's
modulus has not much to do with what we call hardness and measure with hardness tests.
- Elasticity? Wouldn't you rather reserve that word for assessing how much
you can elastically elongate or bend something, and not for how much force you have
to apply for elongating / bending?
Let me help you: |
| | |
| |
We call the material-specific property measured by Young's modulus:
Stiffness
|
|
| |
| |
|
 |
Note right away that what you would conceive as the stiffness
of your blade is probably not the same thing as what I introduced here. What you
might see as the stiffness of your blade depends on two completely unrelated things:
- The specific stiffness of the material it's made from, or Young's modulus of the
material, or what I consider as stiffness only, and:
- The precise cross-section of your blade, or a purely geometrical parameter.
A thick broad blade is "stiffer" of course than a thin and slender one, even so the material for both has
the same stiffness. The dependence of blade stiffness on geometry is "trivial",
however, from a materials point of view. It is just a number you need to get and then it is trivial to use. It's not quite
so trivial, however, to calculate that number. I will deal with that here. |
 |
The important thing is to realize and remember that "stiffness"
as described by the numerical value of Young's modulus has nothing to do with fracture strain,
hardness or ductility. |
|
 |
So a material with a large Young's modulus we would call very stiff material. It might be
hard, too, but you cannot derive the hardness from a known stiffness, just as you cannot tell if a material is silvery or
red from knowing its stiffness. It's just not the same.
Now to the next problem: |
 |
The word "stiff" is used when we describe a large Young's modulus or
a high degree of stiffness. So what do we call a material with a small Young's modulus
like rubber?
Soft? No! |
|
 |
Soft is the opposite of hard—and not the opposite of very stiff.
I must admit that
there is no good name for that. Pick what you like, for example docile, pliant
or resilient. On second thoughts, be careful about resilience.
That name is already taken for the ability of a material to absorb energy when deformed elastically. |
 |
What I'm driving at is that you should be careful about what is meant if somebody
uses well-known everyday words like "strong", "hard", "tough", "stiff", "resilient",
or "soft" for describing mechanical properties of a material. It's often not good enough and prone to cause confusion. |
|
 |
Just to remind you that this is a scientific article, albeit without equations and fancy language,
I will give you now an idea about numbers for Young's modulus. In science we like to be quantitative.
|
| |
|
|
|
|
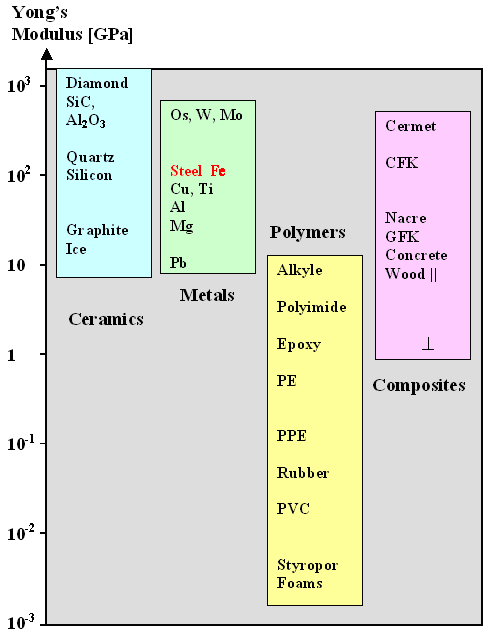
| Young's modulus for some materials - Graphic |
| Material | Diamond | WC | Al2O3 | Al |
Bronze
Brass | Concrete | Glass | Iron
Steel |
Fe3C | | Y (Gpa) | 1220 | »600 |
435 | 69 | 95 - 1120 | »20 |
50 - 90 | 190 - 210 | »200 |
| Young's modulus for some materials - Numbers |
|
| |
| |
 |
What you see is that, yes, hard materials
like diamond or tungsten carbide (WC), taking "hard" for the time being in the regular sense of the word, tend
to have a large Young's modulus. But there are still big differences. |
|
 |
Diamond (C) and Tungsten carbide (WC) are both very hard and both have large but substantially
different Young's moduli. Sapphire, also known as Aluminum oxide (Al2O3, the hard little crystals
on emery paper that scratch most materials when you "sand" them), is also quite hard but has an even smaller Young's
modulus. |
|
 |
Polystyrene ("Styropore") as one representative of the large number of polymers
out there is soft and has a very small Young's modulus.
So, yes again. There is a certain common trend between stiffness
and hardness. But, once more, it is not the same. Far from it—as we will see in
the context of swords right below. |
 |
First, however, I must address the question you might have.
So you wouldn't have thought of polystyrene, or iron (Fe), magnesium (Mg), steel, rubber and so on as being brittle?.
So why did I assign a Young's modulus to them, considering that we are discussing only brittle materials at that moment
and that I only defined Young's modulus as the slope of the stress-strain curve of brittle materials? |
|
 |
If you really ask that question you didn't do your homework - or you got it wrong. I'll come
to that in a minute. |
 |
Now you must, I repeat must
note something quite relevant to our topic here: |
| | |
| |
Pure and rather soft
iron has the same
Young's modulus or stiffness as hard steel!
|
|
| |
| |
|
 |
All steels have the same specific stiffness! I just claim this without giving a reason. Do
you believe me? Yes? You're a sucker. You should believe me, of course, but not without asking: why?
Why do all steels have the same specific stiffness?
I'm
going to tell you why it can't be otherwise - but not before chapter
4.1.3. |
 |
Let's look at some other materials in the figure above. CFC, short for carbon fiber composite, the stuff of modern airplanes, tennis rackets and Formula 1 cars, has
a relatively large Young's modulus compared to GFC, glass fiber composites, the stuff for boat
hulls, swimming pools, and so on. Wood has a small Young's modulus and tooth enamel
and nacre (= mother of pearl) are doing fine compared to magnesium or polymers. Both consist
of high-modulus calcium phosphate or calcium carbonate, respectively, encased in a low-modulus matrix of bio-polymers or
proteins. |
|
 |
Aha - we are talking composite properties here.
Young's modulus of the composite materials given in the table is some average of the moduli of the components and often
much larger than that of the low-modulus matrix.
Pattern welded "damascene" sword blades are usually conceived
to be composite materials of hard and soft steel.
It's not quite true and in any case both steels have the same Young's modulus. Now you
should wonder what advantage this composite technique offers. It is certainly not an
improved stiffness of the blade. |
|
 |
Now don't forget: we are talking Young's modulus here, not
hardness. When we bend a blade elastically, Young's modulus (and its shape) tells us
how difficult that is going to be. We always hope that it deforms exclusively elastically since the only other options are
breakage or plastic deformation (staying bend) and we hate that. |
 |
Bend? By now I have used a new if familiar
term several times for a special kind of deformation. It's time to look at it a bit more closely.
So far I just discussed
mainly tensile testing, straight pulling or pushing. Specimen got longer of shorter but they did not bend. This gave us
Young's modulus. But what does Young's modulus have to do with bending? |
|
 |
Relax. Even so I do not give equations here, you realized; I hope, that with Young's modulus
it is fairly easy and straightforward to calculate what would happen to a specimen if
you pull or push.
It is just as possible, if
far less straightforward, to calculate what would happen elastically to a specimen if you try to bend it or to mutilate
it in other way—as long as you know its Young's modulus (and its shape, of course). |
 |
Now comes the "tough", "hard" or "stiff" question: How does a pattern-welded Celtic "damascene" blade, or a hard-soft-hard cross-section
Japanese sword blade, bend elastically when compared to a geometrically identical blade that is made from uniform soft or
hard steel? |
|
 |
The answer shouldn't surprise you anymore: All blades
with the same cross-section bend pretty much the same way.
Since elastic deformation for a given shape concerns only Young's modulus, and since Young's modulus is the same for all kinds of iron and (carbon)
steels, there is no appreciable difference. |
 |
So what's the advantage of damascene and other tricky techniques? It cannot influence
a swords stiffness and thus its bending behavior. |
|
 |
We have a really tough (sic) question. The answer has to wait for quite a while. First we
need to look at your remaining assignments. This quick reference module
might help |
|
| |
© H. Föll (Iron, Steel and Swords script)


