4.1.3 Young's Modulus and Bonding

You need quantum theory to calculate the bonding between atoms, but you don't need it at all to envision the bonds between atoms. That's because the result of all those calculations is surprisingly simple. The bonds between atoms behave just like tiny little springs connecting the bonded atoms. This is shown schematically in the figure on the right.
Of course, if you look a bit more closely, it is not quite that simple. But as long as we only consider "normal" behavior, like the response to a bit of pulling, we don't have to worry much.

The spring model actually has a lot of explanatory power. Even in serious science we use it for all kinds of involved calculations. This link explains how one should "read" highly stylized figures like the one on the right.
The strength of a spring simply mirrors the strength of a bond. If you want to make your crystal longer or shorter, you must make the springs longer or shorter. You are, in other words, pulling the atoms apart or squeezing them together a bit.
This takes some force, and force times the distance you pulled measures the work you need to do.
Now we have a first magical word: work! Changing the dimensions of your sword requires to do some work.

We all have some direct relation to mechanical work. You know that you do a lot of work if you lug heavy things around, and that you're not doing all that much (mechanical) work when you are sitting at your desk, bending a paper clip back and forth to pass the time. The work needed to do something will be in the center of what follows. But before I go on, you need to appreciate the big magical word now coming up:

Another word for "work" is:

Energy

Assume that the bonding springs will "let go" or break if you pull them out to a large distance. This requires some work, and and the work you need to invest we will not call work but bonding energy.

Chemistry is not only about forming some compounds but also about ripping something apart. Take silicon dioxide (SiO₂), a material rather plentiful on this planet, rip it apart, and you get silicon (Si) and oxygen (O). Doing that takes some work or, as we call it now, energy, and the bonding energy is a measure of how much work you need to do.
In exactly the same way we make iron and many other substances.

Take some iron oxide (e.g. Fe₂O₃ or Fe₃O₄) and rip it apart. On paper you get iron and oxygen; in reality it is bit more complex but that doesn't matter here. The bonding energy between iron and oxygen atoms tells you how much effort, work, or, to use the proper word, energy you must invest in the enterprise.
Take aluminum oxide and rip it apart... OK, you get the drift.

I have credited you with a halfway decent education. So I'm sure you now remember the most important general law concerning the running of this universe:

Energy is conserved!

The energy contained in some system might change from one kind to another one—but never will it increase or decrease.

An immediate consequence is that if it takes some defined amount of energy to rip bonded atoms apart, exactly the same amount of energy must be released if they team up again.

Try it with a mixture of hydrogen and oxygen. You make those atoms by ripping water molecules apart; see above. This takes a lot of energy. The mating of your isolated hydrogen and oxygen atoms then releases exactly that energy rather suddenly, an unforgettable experience for the survivors.
You need to invest the bonding energy for ripping molecules apart and you get exactly the same energy back when they combine. That's why we call that kind of energy also "chemical energy" When you burn your gasoline in your car, you essentially oxidize carbon to CO₂, releasing a lot of chemical or bonding energy because carbon just "likes" to associate with oxygen more than with the partners it had in gasoline (essentially hydrogen).

We are not chemists and we don't like to rip our swords apart. All we might consent to do is to pull at it a little or bend it a little.

In this case we just elongate (or shorten) the bonding "springs" a little bit. We do a tensile test so we invoke Young's modulus.
How about an epiphany now?

Young's modulus measures the
strength of the bonding springs

Of course, Young's modulus is not given by the strength of just one spring. It is rather the force you have to apply to elongate all bonding springs found in an area of 1 cm² by 0.01 %. But that is trivial That's simply the strength of one spring multiplied by the number of springs involved.

So why did Young define the modulus named after him not in terms of bonding? Because he had no idea about atoms and the bonding springs between them. He didn't explain it (as I just did), he just gave a recipe for measuring a useful property. He had no idea why different materials had different Young's moduli while I have just answered this "why" question.

The insight that Young's modulus represents the strength of the bonds between all the atoms in a crystal has a first important consequence for the elastic properties of sword blades.

As long as we have mostly iron - iron bonds in a sword blade, Young's modulus will be about the same.
A few percent of other bonds, for example to carbon atoms in steel, will at best make a difference of a few percent in Young's modulus. This is not open to doubt. It simply can't be otherwise.
The science link will show how to calculate Young's modulus from bonding spring properties in great detail. In addition, it will also show how to calculate a few more properties:

Thermal expansion.
Vibration frequencies of the atoms in a crystal.
Ultimate fracture strength.

Science
Link

Spring model

Did you experience the required epiphany here?

Did you realize that I have answered the first big why question? Why is Young's modulus about the same for all steels as claimed in chapter 3.1?
This so important that I illustrate it below once more just to make sure you get the point.


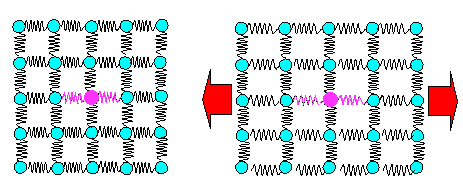Schematic view of bonds = springs and what happens if you deform elastically
All springs get elongated. A few different springs (= bonds to foreign atoms) don't make a big difference.

Why is Young's modulus about the same for all steels, as we noted in chapter 3.1. Because the overwhelming majority of the bonds = springs that determine Young's modulus are iron - iron bonds. The few iron - carbon bonds in steel simply cannot make a big difference.

Understanding this makes our top "why" question even more mysterious:

Why does a little bit of carbon make
no noticeable difference for
elastic deformation
but a tremendous difference for
plastic deformation?

As you know, less than 1 % of carbon turns soft into very hard steel, many times harder than pure iron. And hardness, as you remember, simply measures the onset of plastic deformation
Why?
By the end of the 5th chapter you will know.