Crystal Models

This Hyperscript is full of schematic drawings of crystals. It is not always obvious that these drawings are highly abstract and mostly outright wrong if taken at face values. The reason for this "fraud" is simple. In proper drawings that would show the atoms with their proper relative size and their three-dimensional arrangements, you just wouldn't see a thing anymore.

In what follows a lot of figures illustrate how one one gets from the "real" picture to the stylized ones, and how one should look at those. This link gives some more figures.
For starters we take a simple ionic crystal like sodium chloride (NaCl) or everyday rock salt. The figure below shows a "correct" drawing.

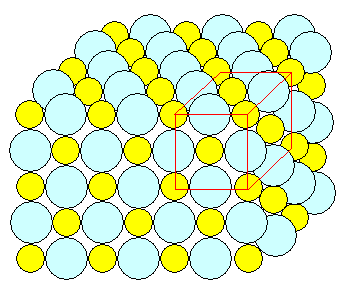	Correct figure Here is a perspective 3-D view of a rock salt crystal, roughly to size. However, it's not quite correct because I did not draw the atoms behind the first "front" layer.

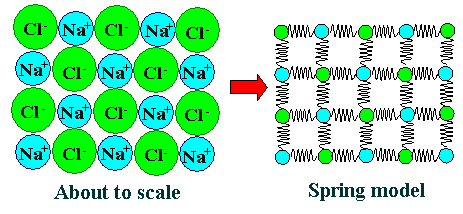Rock salt (NaCl) crystal.
Two-dimensional view and a spring model as first abstraction.

It is clear that most of the time three-dimensional drawings simply produce too much confusion. We need to simplify. The left-hand picture above therefore shows the ions in about the right size relation and the proper arrangement only in a two-dimensional view. The picture now is correct but still not very useful.
We know that the forces between the atoms can be approximated with a spring. So we replace it by the spring model shown on the right-hand side.

That involves an amazing number of simplifications:

Atom / ion sizes are meaningless now.
There is a lot of "free space" between the atoms that is not really there.
The forces between the ions in an ionic crystal are the same in all directions. Showing just 4 springs per atom does not do justice to that. It does justice, however, to the basic 4-fold or cubic symmetry of the real crystal.
There are not enough springs. The whole thing would collapse if you imagine it in three dimensions; see below
The ions are not sitting still but vibrate vigorously at room temperature.

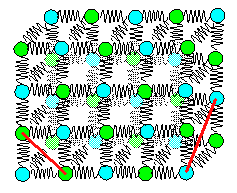Three dimensional spring model
Without diagonal springs along directions as indicated by the red lines, the crystal would collapse.
That means that we also have to look at the forces between second-nearest neighbors.

Let's see what we can do about the last point in the list above; the fact that those atoms vibrate. Here is an attempt at a spring model with vibrating atoms / ions.

	Well, whatever that figure shows, it is not really showing vibrating atoms. How would you draw that? Like in this link? The long and short of this is that you simply can't come up with a drawing that does justice to the vibrations.
Spring model with vibrating atoms?

What the figure above attempts to show is what vibrating (stylized) atoms look like if you take a snapshot with an extremely short exposure time (around 10^-14 s or 10 fs). The atoms then are somewhat deflected from their zero position in a random way.
Or are they? Well, they are deflected but not in a random way as far as individual atoms go. A better way to "draw" vibrating atoms, if we must, is shown below.


"Synchronized" atom vibrations called "phonons"

The atoms don't vibrate completely randomly. They synchronize to some extent as shown schematically above and that simply means that "elastic waves" with a spectrum of wavelengths, amplitudes and directions are running through the crystal. Those waves, care called "phonons". They get reflected at boundaries like the surface or at grain boundaries, scattered at defects, and so on.
In short, they behave pretty much like the light waves that are running around in the room you are in right now.

Obviously, drawing vibrating atoms in whichever way does not help us much in modelling crystals by using schematic figures. I will never do it again.

Now let's look at another problem. While for ionic crystals like rock salt, and pretty much for all metals, the bonding forces are the same in all directions, this is not true for many other "covalently" bonded crystals like silicon (Si), diamond (C) or silicon dioxide (SiO₂). Those atoms attract each other only along some well-defined directions.

This sounds great because now a few springs could symbolize the real bonds quite well. Of course, there is also a problem. Let's look at the figure below to appreciate this.


Red lines symbolize bonds / springs	Black lines symbolize the lattice
Diamond type crystal

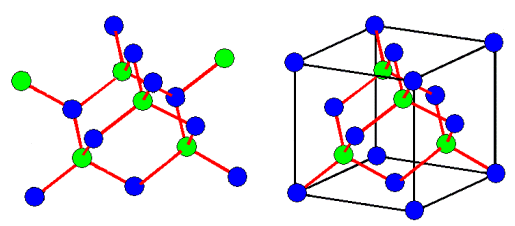
On the left we have a model of all diamond type crystals. Since it is time consuming to draw a lot of springs, I simply substituted a red line for a spring. The problem is obvious: you don't recognize the cubic lattice of the structure.
This is shown on the right-hand side in addition to the red bond "springs". Of course, the black lines are completely meaningless in terms of the real structure, they simply "guide the eye".

You get it by now. Crystal models are always highly abstract and just show part of what is really there. Nevertheless, they are highly useful and indispensable. Let's look at a few examples.

Science Link

Calculations

Here is the spring model for looking at Young's modulus qualitatively . How you calculate it and other properties quantitatively is shown in a science module.
The following figures just illustrate in a qualitative way how one should look at things for proper quantitative calculations. More than that those models cannot do.

$Spring model, Young's modulus and fracture$
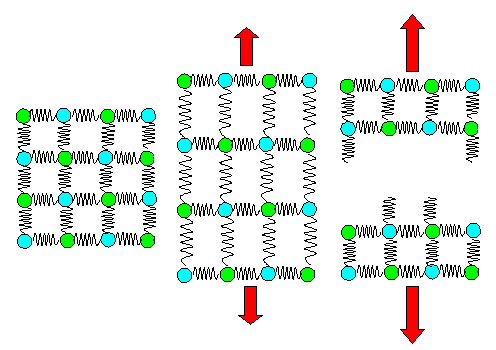Elastic deformation and eventual fracture in the spring model.

Here we see how to start calculating elastic behavior expressed in Young's modulus. We just need to look at how those springs elongate if we pull a them. How that is done with equations is shown in the science module.
We also have (brittle) fracture covered. As soon as your springs are completely pulled out, any further elongation must result in the springs breaking. The two crystal pieces left back are "relaxed" again, i.e. the length of the springs has the old values of an undeformed crystal. Putting that in equations needs a bit of thought but is perfectly possible.

However, what the model above does not show is the effect of lateral contraction, the phenomenon that the specimen gets thinner as it gets longer. This is dealt with phenomenologically in this science module.
The spring model above doesn't show this effect nor should it - so why does that happen?
Because the spring model above is too simple. As noted before, for a stable crystal we need to consider that there are diagonally springs to second-nearest neighbors, too. If we draw this into the picture it gets a bit unwieldy but makes clear what happens:


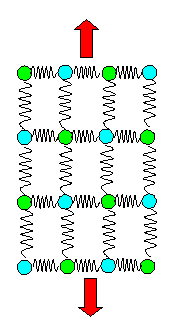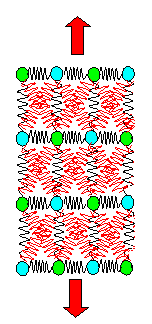Spring model without and with lateral contraction.

The "red" springs, if elongated, will also pull the atoms somewhat inwards; the specimen gets thinner. With that qualitative picture in mind, we now could start some calculations.

The long and short of this module is: