|
Two-dimensional defects like stacking faults, but, to some extent also grain-
and phase boundaries, give rise to some special contrast features. |
|
 |
Stacking faults are best seen and identified under dynamical two-beam condition; i.e. the
Bragg condition is exactly met for one point in the reciprocal lattice. |
|
 |
This automatically implies that the diffracted beam, if seen as the primary beam, also meets the Bragg
condition; it is diffracted back into the primary beam wave field. |
|
 |
This leads to an oscillation of the intensity between the primary and the diffracted beam as a function
of depth in the sample; the "wave length" of this periodic intensity variations is called the extinction length
x. |
 |
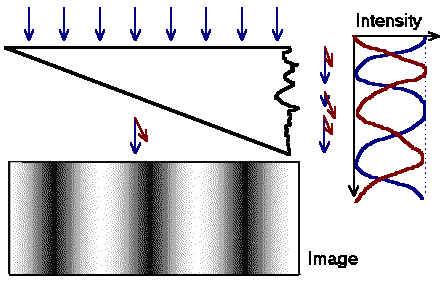
For a wedge-shaped specimen, the intensity of the primary or diffracted wave thus
changes with the local thickness; it goes through maxima and minima. |
|
 |
The illustration shows the resulting image: a system of black and white fringes, called thickness fringes
or thickness contours is seen on the screen.On top a schematicdrawing, on the bottom
the real thing. In this case it is an etch pit in a Ge sample which is the usual inverted pyramid with {111}
planes. |
| |
|
 |
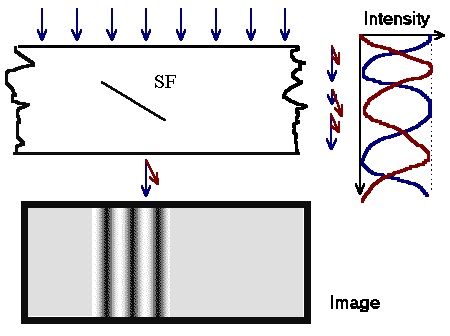
A stacking fault can be seen as the boundary between two wedge shaped crystals
which are in direct contact, but with a displacement R along the wedge. |
|
 |
As a result, the two fringe systems resulting from the two wedges do not fit together anymore. A new fringe
system develops delineating the stacking fault; we see the typical stacking fault fringes |
| |
|
|
 |
Again, getting all the signs right, the nature of the stacking fault can be determined. If intrinsic stacking
faults under some imaging conditions would start with a white fringe, extrinsic stacking faults would start with a black
one. Reversing the sign of the diffraction vector g or the displacement vector R changes white
to black and vice versa. |
 |
If more kinematical conditions are chosen, the amplitude of the intensity oscillation
decreases; the stacking fault contrast assumes an average intensity that is usually different from the normal background
intensity - stacking faults appear in grey. |
 |
A few examples: The picture below shows three defects that behave as predicted and could be
stacking faults. Indeed, the small defect in the top half and the very large defect are stacking faults. The smaller defect
in the bottom part, however is a micro twin. This is not evident from one picture, but can
be concluded from contrast analysis. |
| |
|
 |
The next picture shows a complicated arrangement of several stacking faults: |
| |
|
|
 |
A whole system of overlapping oxidation induced
stacking faults in Si. The biggest loop was truncated by the specimen preparation; the fringe system where
the stacking fault intersects with one surface is clearly visible. |
|
 |
The other surface was preferentially etched; the etch pits down the (Frank) dislocation lines are clearly
visible. |
|
 |
The overlap of several stacking faults leads to changing background contrasts - from black to no contrast
(whenever multiples of three stacking faults overlap) to almost white. |
|
 |
Similar if less complicated contrast effects were already encountered in illustrations
given before in the context of point defect agglomeration. |
|
 |
More examples of a typical oxidation
induced stacking faults in Si (OSF) are given in the link |
 |
But there are limits to TEM analysis: Sometimes defects are observed which resist analysis.
One example is shown in the link; another one we will encounter in the
next subchapter. |
| |
|
Other Defects |
| | |
 |
The strain-induced contrast of dislocations due to local intensity variations
in the primary and diffracted beams and the fringe contrast of stacking faults due to local phase shifts of the electron
waves, if taken together, are sufficient to explain (quantitatively) the contrast of any defect. |
|
 |
It may get involved, and not everything seen in TEM micrographs will be easily explained, but in
general, contrast analysis is possible and the detailed structure of the defect seen can be revealed within the limits of
the resolution (you cannot, e.g., find a kink in a dislocation
(size ca. 0,3 nm) with a typical kinematical bright field resolution of 5 nm). |
 |
In the links a gallery of micrographs is provided with a wide spectrum of defects.
Bear in mind that most examples are from single crystalline and relatively defect free Silicon. The images of regular poly-crystalline
materials would be totally dominated by their grain boundaries (see the examples at the end of the list). |
|
 |
Small dislocation loops in Cobalt produced by ion-implantation. |
|
 |
Precipitates in Silicon with dislocation structures. |
|
 |
Needle shaped FeSi2 precipitates in Si;
the bane of early IC technology. |
|
 |
Helical dislocations resulting from the climb of screw
dislocations. |
|
 |
Bowed-out dislocations in a TiAl alloy; kept
in place by point defects and small precipitates. |
|
 |
A thin film of PtSi
on Si as an example of the "real" world of fine-grained materials. |
|
 |
Overview of TiAl as an example of a specimen
with a high defect density. |
© H. Föll (Defects - Script)