|
In most crystals and under most circumstances
there is no such thing as a straight dislocation. Real dislocations contain kinks
and jogs - sudden deviations from a straight line on atomic dimensions. |
 |
These defects within a defect may strongly
influence the mobility of dislocations and are thus of importance. |
|
 |
They owe their existence first of all to the fact that dislocations always "live"
in a crystals - in a periodic arrangement of atoms. We have not used that fact so far, except in a rather abstract way for
the very definition of dislocations with the Volterra cut. Now it is time to appreciate
the effects of the crystal on the fine structure of dislocatons. |
|
 |
Kinks (and jogs) may be produced by several mechanisms, in particular they may be formed by the movement of the dislocation. |
 |
First, let's look at kinks. For that we first have to consider
the concept of the Peierls
potential of a dislocation. |
|
 |
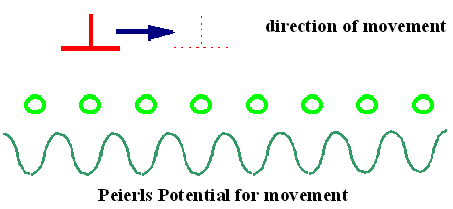
Consider the movement of an edge dislocation as shown below. The green circles symbolize the last atom
on the inserted half- plane of an edge dislocation. In local equilibrium its distance to the atoms to the left or right
will be same for basic reasons of symmetry, cf. the perspective drawing
of an edge dislocation. |
| |
|
|
 |
If the dislocation is to move, the last atom (and the ones above to some extent) has to press against the
neighboring atom on one side and move away from the atom on the other side. That is clearly a situation with a higher energy
which can be cast into a potential energy curve as shown in the illustration. At some point when both lattice plans are
most affected, there is a maximum and a new minimum as soon as the dislocation has moved by one Burgers vector. The minima
and maxima of this Peierls potential are along directions of high symmetry. |
|
 |
To overcome the maximum of the Peierls potential, the stress has to be larger than some intrinsic critical shear stress
tcrit. |
 |
The Peierls potential defines special low-energy directions in which the dislocation
prefers to lie. This is the third rule for directions that dislocations like to assume!
(Try to remember the first and second rule, or use the links).
|
|
 |
In other words, the inserted half-plane for the easy-to-imagine case of an edge dislocation should be clearly
defined and should be in a symmetric position between its neighbour planes - exactly
as we always have drawn it. |
|
 |
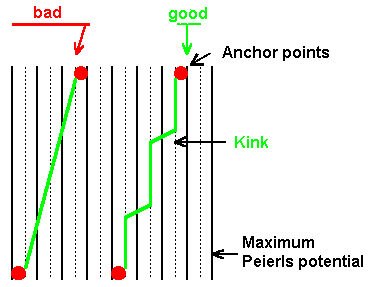
A dislocation that is almost, but not quite an edge dislocation, thus would prefer to be a pure edge dislocation
over long distances and concentrate the "non-edginess" in small parts of its length as shown below. The same is
true for screw dislocations, even so it is not quite as easy to contemplate. |
| |
|
|
 |
The dislocation runs in the minima of the Peierls potential as long as possible and then crosses over briskly
when it has to be. The transition from one Peierls minimum to the next one is called a kink
as shown in the picture above. |
 |
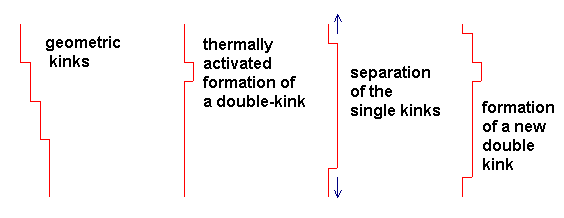
The kinks that come into existence in this way are called geometric
kinks. But there is also a second kind, the thermal equilibrium (double)-kink,
i.e. a crossing over to a neighboring Peierls valley followed by a "jump" back. |
|
 |
A kink, or better a double-kink, is simply a defect in an otherwise straight dislocation line, adding some
energy and entropy. Since the formation
energy of a double kink is not too large, they will be present in thermal
equilibrium with concentrations following a standard Boltzmann distribution. |
|
 |
To make that perfectly clear: While a dislocation by itself is never in thermal equilibrium, i.e. will
never form spontaneously by thermal activation, this is not true for the defects it may contain. Double-kinks, seen as defects
in a dislocation line, form and disappear spontaneously, if sufficient thermal energy is available; their number or density
thus will follow a Boltzmann distribution. |
|
 |
Once a thermal double-kink has been formed, the two single kinks may move apart; if the process is repeated,
we have a new mode of dislocation movement for an otherwise perhaps immobile dislocation.
This is shown below. |
| |
|
 |
Kinks then are steps of atomic dimension
in the dislocation line that are fully contained in the glide plane of the dislocation |
|
 |
With this general definition, we can consider kinks in all dislocations, not just edge dislocations. |
 |
Screw dislocations have a Peierls potential, too, and thus they may contain kinks.
The kink, per definition, is then a very short a piece of dislocation with edge character.
|
|
 |
This has far reaching consequences: A screw dislocation with a kink now either has a specific glide plane
- the glide plane of the kink - or the kink is an anchor point for the screw dislocation. |
|
 |
Kinks can do more: As indicated above, at not too low temperatures when the generation of thermal double
kinks becomes possible, the applied stress may be below the critical shear stress needed to move the dislocation in toto
(i.e. move it across the Peierls potential), but might be large enough to separate double kinks and thus promote dislocation
movement and plastic deformation. We have one of several effects here that make crystals "softer" at high temperatures. |
 |
The best way to investigate kinks are internal
friction experiments. |
|
 |
An oscillating deformation is chosen, e.g. by vibrating a thin specimen driven by an electromagnetic field.
The amplitude and thus the internal stress and strain are easily measured. As long as the stress is not too large, deformation
proceeds by the generation and the movement of kinks. This is a fully reversible process and the response to an external
stress thus is purely elastic even though a dislocation moved! |
|
 |
However, in contrast to elasticity just coming from stretching the bonds between the atoms, the generation
and movement of double kinks takes time and is strongly temperature dependent. Specific time constants are involved and
a peculiar frequency dependence of the elastic response will be observed which contains information about the kinks. |
| | |
 |
The term "Jogs" is sometimes considered to
be the term for all "breaks" or steps in a dislocation line with atomic dimensions. Kinks then would be a subclass
of jogs with the speciality of being in the glide plane. |
|
 |
However, it is customary to use the term "jogs" for all steps
that are not contained in the glide plane. Looking just at the inserted half-plane of an edge dislocation, jogs
and kinks would look like this: |
|
|
|
|
 |
But remember: Jogs and kinks can occur in any dislocation, not just edge dislocations - they are just not
as easily drawn! |
 |
Jogs in edge dislocations are obviously prime places for the emission or absorption
of point defects as is shown in the next illustration which looks at the inserted half-plane of an edge dislocation. |
| |
|
|
 |
The movement of jogs by emission or absorption of point defects means that the dislocation
moves. This particular process of dislocation movement is called climb of dislocations.
It is a movement that does not take place in the glide plane of the dislocation. |
 |
Generally speaking, we define: |
|
 |
Conservative movement of dislocations = movement
in the glide plane = glide (for short) = movement without assistance of point
defects. |
|
 |
Non conservative movement of dislocations =
movement not in the glide plane = climb (for short) = movement needing the
assistance of point defects. |
| |
|
 |
How do kinks and jogs come into existence? Three mechanisms can be identified. |
|
 |
1. Thermally activated generation of double kinks as discussed
above. |
|
 |
2. Thermally induced generation of jogs
by absorption or emission of point defects. This mechanism is thermally induced (and
not "activated") because it responds to a super- or undersaturation of point defects. At large under- or supersaturations,
the process becomes more likely. Here we have one of the source/sink processes needed for point defect equilibrium. |
|
 |
3. Intersection of dislocations |
 |
The last process is new and needs some explanation. Lets look at the movement
of an edge dislocation in the following geometry: |
|
|
|
|
 |
The intersection of the edge dislocation with the screw dislocation produces one jog each per dislocation.
(Consider the cut-and-move procedure and you will see why). It is clear that the same thing happens for the intersection
of arbitrary mixed dislocations - a jog characterized by the Burgers vector of the dislocation that moved across will be
generated. |
 |
This gives us a general relation and explains to some extent why plastic deformation
is an extremely non-linear process: |
|
 |
Movement of dislocations generates jogs. |
|
 |
Jogs influence severely the movement of dislocations - so there is
some feedback in the process of plastic deformation, and feedback of any kind is the
hallmark of non-linear processes. |
 |
Considering jogs and kinks (together with knots), we start to consider real dislocations - and its getting complicated. |
|
 |
And don't forget: All those great electron microscope pictures showing all kinds of dislocations,
never show the jogs and kinks! They are simply too small. So even dislocation that look
like perfect straight lines in a TEM picture, may be full of jogs and kinks. |
| | |
 |
There is one last property induced by these defects in a defect: |
|
 |
Jogs, kinks and their combinations may produce "debris" left behind
by a moving dislocation, because it is often "better" for dislocations to tear away from immobile parts like jogs,
leaving behind a trail of point defects which in turn may agglomerate. |
|
 |
If the jog is large extending over several lattice planes, a whole trail of small dislocation loops may
form. The formation of a trail of vacancies in the wake of a jogged moving
screw dislocation is illustrated in the link |
|
| |
|
 |
Some more text to come - but try the exercise anyway! |
| |
|
© H. Föll (Defects - Script)