|
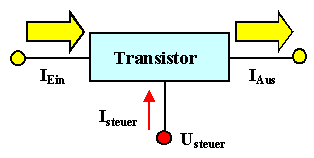
Ein Transistor ist ein festkörperelektronisches
Bauelement, mit dem man Strom zwischen zwei Anschlüssen durch Strom oder Spannung an einem dritten Anschluß ein- und auschalten kann.
|
|
 |
Wir haben damit immer drei Anschlüsse,
das sieht grundsätzlich so aus: |
|
|
|
 |
Ströme und Spannungen am Ausgang sind immer viel größer als die
Spannungen und Ströme, die man zum Steuern, d.h. zum Ein- und Ausschalten braucht. |
|
 |
Damit kann man also grundsätzlich eine Leistungsverstärkung
erzielen. Man kann das auch analog tun, d.h. die Ausgangsgröße folgt (mit
Glück halbwegs linear) der Steuergröße. Aber in dieser Vorlesung sind wir digital,
wir schalten den Ausgangsstrom nur ein und aus. |
 |
Ein elektromechanisches Relais macht im Grundsatz
dasselbe. Es ist aber kein Transistor! Und das nicht so sehr weil es kein festkörperelektronisches Element ist, sondern weil es die wesentlichen Sekundärtugenden
eines Transistors nicht hat. Diese sind: |
|
 |
1. Alles ist elektronisch - nichts
bewegt sich mechanisch. Die gute alte Elektronenröhre, z.B. in der einfachsten Form einer Triode,
hat diese Tugend aber auch. |
|
 |
2. Das Ein- und Ausschalten geht sehr schnell.
So einige Milliarden mal pro Sekude - d.h. mit > 1 GHZ - sollte es schon sein. Die gute alte
Elektronenröhre macht das nicht mehr - die gute neue aber schon (z.B. in der "Mikrowelle"). |
|
 |
3.
Sparsamkeit - das ganze funktioniert bei minimaler Leistung, insbesondere im "off"
Betrieb. Die Elektronenröhre hat jetzt massive Probleme, da ihre Heizung immer laufen muß. |
|
 |
4. Kleinheit - allenfalls noch 1 µm ×
1 µm × 0,3 µm ist der Transistor groß. Die Elektronenröhre ist jetzt out. |
|
 |
5.
Integrationsfähigkeit - wir können viele Millionen Transistoren in einem Silizium Chip machen und verbinden, z.B.ca 300 000
000 Transistoren (plus 256 000 000 Kodensatoren) in einem 256 Mbit Speicherchip. |
 |
Wenige Erfindungen haben die Welt so verändert wie der Transistor. Und unter
allen weltverändernden Erfindungen ist er die erste (oder, falls man die Atombombe mitzählt), die zweite, die
auschließlich auf "Theorie" beruht und nicht auf "Tüfteln", wie z.B. das Rad, die Schrift,
der Buchdruck, die Elektronenröhre, das Auto, die Herstellung von Stahl oder die sexuelle Revolution. |
|
 |
Es gibt zwei Transistorgrundtypen: Den MOS-Transistor, und den bipolaren
Transistor. Der MOS-Transistor
ist der weitaus häufigere, aber für uns noch nicht ganz einfach zu verstehen. |
|
 |
Mit dem bipolaren Transistor aber haben wir kein Problem;
ihm widmen wir dieses Unterkapitel. |
|
| |
|
Der bipolare
Transistor |
| |
|
 |
Ein bipolarer Transistor besteht aus zwei hintereinander geschalteteten
pn-Übergängen; hat also eine p-n-p oder n-p-n Struktur, wobei die mittlere Schicht sehr dünn sein muß. (Das konnte man sich damals leicht merken: Der p-n-p Transistor
hat den gleichen Aufbau wie die Mensa Schnitzel der sparsamen 60er Jahre: Paniermehl - Nichts - Paniermehl).
Jede Schicht hat einen elektrischen Anschluß. |
|
 |
Zwei hintereinandergeschaltete Dioden bilden keinen bipolar
Transistor, denn sie sind, erstens, keine p-n-p oder n-p-n Schichtung sondern z.B. eine p-n-Metall - Metall-n-p
Schichtung; und damit ist, zweitens, die mittlere Halbleiterschicht nicht dünn. |
|
 |
Ein bipolar Transistor ist schematisch wie unten gezeigt
aufgebaut. In der Realität sieht er ziemlich anders aus, das ist in einem extra
Modul dargestellt. |
| |
|
|
 |
Wir unterstellen ohmsche Kontakte
zu allen drei Bereichen. Der zu steuernde Strom fließt vom Emitter zum Kollektor, durch die steuernde Basis hindurch. |
|
 |
Die Grundbeschaltung ist eingezeichnet: Wir polen immer
die Emitter-Basis Diode in Vorwärtsrichtung, und die Basis
-Kollektor Diode in Rückwärtsrichtung. |
|
 |
Der externe Strom fließt dann von Plus nach Minus,
wie eingezeichnet. An dem Basisknoten muß die Summe der Ströme = 0 sein; graphisch heißt das, daß
die Gesamtlänge von Kollektor- und Basisstrompfeil gleich sein muß zur Länge des Emitterstrompfeils. |
 |
Um zu sehen, daß diese Anordnung tatsächlich ein Transistor im obigen
Sinne ist, müssen wir jetzt nur das Banddiagramm betrachten. Wir zeichnen es gleich für die beschaltete Anordnung
mit Stromfluß; die Fermienergien sind dann nur Markierungshilfen |
| |
|
 |
Die Emitter-Basis Diode ist in Vorwärtsrichtung
gepolt; es wird also ein großer Vorwärtsstrom jF(BE) fließen müssen. |
|
 |
Dieser Vorwärtsstrom besteht aus Löchern, die
von dem p-dotierten Emitter in die n-dotierte Basis fließen, und aus Elektronen,
die aus der Basis in den Emitter laufen; beide Ströme zusammen bilden den Emitterstrom IE.
(Wir verwenden "I " hier für externe , und "j "
für interne Ströme oder Stromdichten) |
|
 |
Damit gilt als erste Gleichung |
|
|
| IE |
= |
jF(BE) | =
| j eF(BE) + j
hF(BE) |
|
|
 |
Dabei haben wir aber eine kleine Näherung gemacht: Wir haben die Rückwärtströme vernachlässigt. Das machen wir zwar schon ziemlich routinemäßig; aber man sollte sich doch klar darüber sein. Wir wollen
das jetzt durchgehend so machen: Alle "kleinen" Ströme lassen wir weg. |
 |
Der Basis-Kollektor-Kontakt ist in Rückwärtsrichtung gepolt.
|
|
 |
Hätten wir nur diese Diode, würde ein kleiner
Rückwärtsstrom fließen, zusammengesetzt aus den Löchern, die als
Minoritätsladungsträger in der Basis vorhanden sind, an die RLZ-Kante kommen und dann die Potentialschwelle
hinauffallen sowie den Elektronen des Kollektors, die den Berg hinunterfallen. |
 |
Der springende Punkt beim Bipolartransistor ist nun aber die Bedingung, daß
die Basis dünn sein muß, oder genauer gesagt, die Basisweite dB
muß sehr viel kleiner sein als die Diffusionslänge L der Minoritäten in der Basis. |
|
 |
Dann werden die meisten der vom Emitter in die Basis emittierten
oder injizierten Löcher nach kurzer Wanderung im feldfreien Bereich der Basis an
die RLZ-Kante des Basis Kollektorkontakts kommen - und dann selbstverständlich den Berg hinauffallen! |
|
 |
In anderen Worten: Der Beitrag der Löcher aus der Basis zum Rückwärtsstrom
ist massiv erhöht. Fast alle Löcher, die als Komponente des Vorwärtsstroms
vom Emitter in die Basis fließen, werden es bis zum Kollektor schaffen. Der Kollektorstrom IC
besteht damit praktisch nur aus dieser Komponente. In anderen Worten: |
| |
|
|
 |
Der Kollektorstrom wird allerdings ein wenig kleiner sein müssen, als die Löcherkomponente
des Emitter-Basis Vorwärtsstroms, denn ein paar wenige der in die Basis injizierten
Löcher werden dort rekombinieren. Diesen Effekt können wir aber (weiter unten) leicht berücksichtigen. |
|
 |
Erst aber schauen wir uns jetzt das komplette Strombild des bipolar Transistors
an: |
| |
|
 |
Sieht kompliziert aus, aber ist ganz einfach - wieder nur eine Frage der korrekten
Strombuchhaltung. |
|
 |
Zunächst sehen wir, daß der größte Teil des Löcherstroms des Emitters
weiterfließt zum Kollektor, und dort den ganzen externen Strom IC verursacht. |
|
 |
Die einzige offene Frage ist allenfalls, wie aus einem Löcherstrom
im Halbleiter jetzt ein Elektronenstrom im Metall wird. Das ist aber einfach: Das Metall
injiziert Elektronen ins Valenzband, die dort mit den Löchern rekombinieren - es ist schließlich mit dem negativen Pol der Spannungsquelle (= Elektronenpumpe) verbunden. Im Link ist das noch ein bißchen
ausführlicher erläutert. |
|
 |
In der dünnen Basis rekombiniert nur ein kleiner Teil der Löcher und Elektronen;
dies ist schematisch gezeigt. |
 |
Im Emitter fließt aber auch noch der aus der Basis kommende Vorwärtsstrom
der Elektronen. Er wird jetzt wichtig. |
|
 |
Sobald die aus der Basis kommenden Elektronen im p-dotierten Material des Emitters
sind, werden sie als Minoritäten rekombinieren. Im Abstand von etwa L von der Basis sind sie verschwunden,
und es fließt jetzt ein reiner Löcherstrom. |
|
 |
Der Emitterkontakt rekombiniert wieder alle Löcher durch Elektroneninjektion; am Basiskontakt
werden die benötigten Elektronen durch den Kontakt direkt geliefert. |
 |
Auch im Banddiagramm sind die Ströme eingezeichnet. Es wäre jetzt auch
kein Problem mehr, die "kleinen" Ströme noch mitzunehmen - aber es wird nicht viel ändern. |
|
 |
Die Steuerfunktion ist jetzt klar. Mit einer relativ kleinen Vorwärtsspannung an der
Emitter-Basis Diode (» 1 V), kann man einen relativ großen Strom (< 10
A/cm2) über einen relativ großen Potentialunterschied schicken (Die Basis-Kollektor Spannung kann
bis zu 1000 V betragen!). Damit kann man erhebliche Leistungen mit kleinem Aufwand ein- und ausschalten, oder auch
analog steuern (wenn auch nichtlinear). |
|
 |
Aber wir müssen einen Preis dafür zahlen: Leistungslos
funktioniert die Steuerung nicht - denn wir brauchen immer auch einen Basis-Emitter Strom! |
|
 |
Damit erhebt sich die Frage nach der erreichbaren Stromverstärkung
in einem bipolaren Transistor, dem Verhältnis von Kollektorstrom zu Basisstrom. |
| |
|
|
Stromverstärkung des bipolaren Transistors |
| | |
 |
Die Stromverstärkung b
ist definiert als |
| |
| b = |
IK
IB |
= | j
hR(BK)
j eF(BE) |
= | j
hF(BE)
j eF(BE) |
|
|
 |
Das ist nun einfach auszurechnen. Wir nehmen die Formeln
für die Vorwärtsströme aus der (einfachen) Diodengleichung und setzen sie ein. Damit erhalten wir |
| |
|
|
 |
Dabei haben wir großzügigerweise die Diffusionslängen L, die
Diffusionkoeffizienten D (und damit die Beweglichkeiten µ) in der Basis und im Emitter gleichgesetzt,
was zwar nicht ganz korrekt ist, aber die Sache doch sehr vereinfacht. |
 |
Wir haben ein monumentales Ergebnis: Die Stromverstärkung in einem bipolar Transistor ist in guter Näherung nur durch das Verhältnis
der Dotierstoffkonzentration in Emitter und Basis gegeben! |
|
 |
Wir brauchen einen hochdotierten Emitter und eine schwach dotierte Basis, um eine große
Stromverstärkung zu erzielen. Das ist einfach zu machen; b > 100 ist leicht zu
erzielen. |
|
 |
Da die Leistungsverstärkung durch b
· UBK/UEB gegeben ist, kommen wir hier schnell auf Werte b
> 1000. |
 |
Wir brauchen also eine möglichst asymmetrische
Diode, mit möglichst großem Unterschied in den Vorwärtsstromkomponenten. |
|
 |
Das kommt nicht nur dem Bauprinzip der realen
Diode entgegen, sondern ist auch für andere Bauelemente wichtig. Man hat deshalb dem Verhältnis der Vorwärtsströme
einen Namen gegeben, es heißt Injektionsverhältnis, weil ja jede Komponente
für sich als Injektion von Minoritätsladungsträgern
in das jeweils andere Gebiet aufgefaßt werden kann. |
|
 |
Der Vorwärtsstrom einer Diode wird damit zu der Summe der beiden Injektionsströme. |
 |
Jetzt wollen wir aber noch schnell ausrechnen was passiert, falls die Basis nicht
dünn genug ist. |
|
 |
Dann wird der Kollektorstrom gegeben sein durch den Injektionstrom
des Emitters (man kann doch flüssiger schreiben mit diesen Begriffen) minus dem Rekombinationsstrom in der
Basis. |
|
 |
Der Anteil der Minoritäten, die durch die Basis durchwandern können, ist aber einfach
1 – dB/L - man muß nur das "Rekombinationsdreieck" im Emitter im obigen
Bild auch für die Basis betrachten und durch eine Formel beschreiben. |
|
 |
Damit bekommen wir für die Stromverstärkung |
| |
| b = |
NA(E)
ND(B) | · |
æ
è |
1 – |
dB
L |
ö
ø |
|
|
 |
Eine noch bessere Formel ist sinnlos, denn bei realen Transistoren überwiegen
sowieso die nicht berücksichtigten Einflüsse der extrem endlichen Größe in allen Dimensionen. |
|
 |
Insbesondere darf man die "kleinen" Ströme, also die jeweiligen Rückwärtsströme,
nicht ganz vernachlässigen. Zwar spielen sie für den "Ein" Zustand des Transistor-Schalters keine Rolle,
wohl aber für den "Aus" Zustand. |
|
 |
Denn auch wenn alle 100 Millionen oder so Transistoren auf dem Chip "aus"
sind, zieht der Chip noch Strom - 108 mal die Rückwärtsströme der Dioden. Und das addiert
sich dann so allmählich schon zu einem Problem. |
 |
Trotzdem, von den oben erwähnten Kriterien
hat der bipolar Transistor alle erfüllt - außer vielleicht der Forderung nach Geschwindigkeit. |
|
 |
Wie schnell kann man einen bipolar Transistor hin- und herschalten? Das ist eine nicht ganz
triviale Frage, aber eines ist sicher: Man muß nach dem Abschalten mindestens so lange bis zum Wiederanschalten warten,
wie die Minoritäten brauchen, um durch die Basis zu laufen. |
|
 |
Wie "schnell" sind die Minoritäten? Ihre "Durchschnitts"geschwindigkeit
über alles ist jedenfalls vMin = L/t, denn nach ihrer Lebensdauer t sind eine Diffusionlänge L weit gekommen. Mit entsprechenden Umrechnungen erhält man |
| |
| vMin = ( |
kB · T · m
e · t |
)½ |
|
|
 |
Obwohl die Geschwindigkeitskomponente in Richtung Kollektor sicher kleiner ist
als die oben ausgeführte ungerichtete Geschwindigkeit, gibt diese Gleichung doch Hinweise: |
|
 |
Wir wollen eine möglichst hohe Beweglichkeit m und
eine möglichst kleine Lebensdauer t - außerdem hohe Temperaturen? |
|
 |
In Prinzip ja - aber: Kleine Lebensdauern bedingen kleine Diffusionlängen und das bringt
Probleme. Hohe Temperaturen erst recht. Was bleibt ist: |
|
 |
Die maximalen Schaltfrequenzen steigen mit der Beweglichkeit. |
|
 |
Damit ist für extrem hohe Frequenzen GaAs
dem Si überlegen (und wird auch für Hochgeschwindigkeitsschaltungen verwendet). |
 |
Aber auch mit Si lassen sich mühelos die Gigahertze erreichen - denn
die Transitzeit, die Zeit um durch die Basis zu wandern, ist
halt auch immer umgekehrt proportional zur Dicke der Basis- und die ist sehr sehr klein! |
| |
|
© H. Föll (MaWi 2 Skript)