6.3.2 Schottky Kontakte und Ohmsche Kontakte

Der Halbleiter-Metall Kontakt unter Spannung

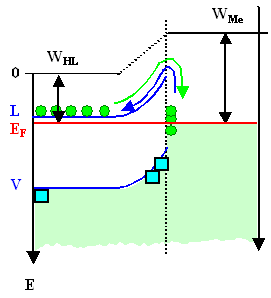
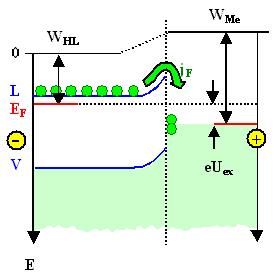
	Im Grunde ist klar was zu tun ist: Wir nehmen die Gleichgewichtsbanddiagramme und verschieben beide Seiten etwas - um – eUex; mit Uex als externe Spannung. Dazu müssen wir nur die Bildserie des vorhergehenden Unterkapitels weiterführen. Als erstes schauen wir uns die Gleichgewichtsstruktur noch einmal an:
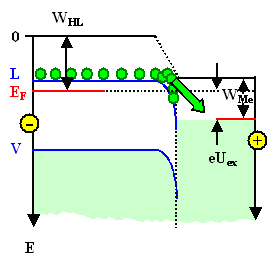
		WHL < WMe		WHL > WMe
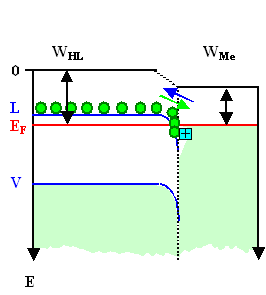
	Jetzt legen wir den positiven Spannungspol an die Halbleiterseite. Damit sinkt sie im Potential (oder die Metallseite steigt). Das sieht so aus:
		Hier ist die Energiebarriere aus Sicht der Elektronen des Halbleiters größer; der Strom der Elektronen aus dem Halbleiter in das Metall versiegt. Aus Sicht des Metalls ändert sich nichts.			Hier haben die Elektronen des Metalls keine Probleme, in den Halbleiter überzutreten; der entgegengesetzte Strom wird aber schnell auf Null fallen.
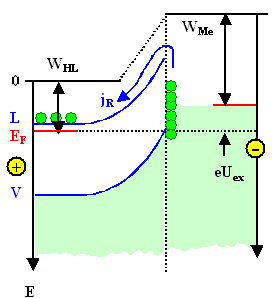
		Netto bleibt jetzt nur der Strom der Elektronen aus dem Metall in den Halbleiter. Er kann nicht sehr groß sein, denn auch er muß über eine Energiebarriere fließen, deren Höhe sich aus der Differenz der Austrittsarbeiten bestimmt. Damit hängt er zwar von der Materialkombination, aber kaum von der angelegten Spannung ab.			Stromfluß ist aus Sicht des Kontakts fast unbegrenzt möglich; letztlich werden die ohmschen Widerstände begrenzend wirken.
		In Dioden"lingo" ist das also der "Rückwärtsstrom".			Im wesentlichen "sehen" wir in diesem Ast der Kennlinie einen exponentiell mit der Spannung anwachsenden Strom, nur begrenzt durch den (kleinen) ohmschen Widerstand des Systems.
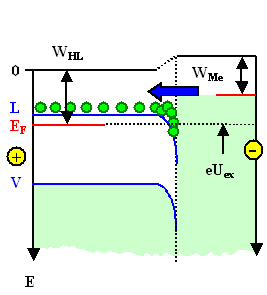
	Jetzt polen wir um und legen wir den negativen Spannungspol an die Halbleiterseite. Damit steigt die potentielle Energie der Halbleiterseite (oder die der Metallseite sinkt). Das sieht so aus:
		Die Energiebarriere sinkt und der Elektronenstrom vom Halbleiter in das Metall steigt, wie beim pn-Übergang, exponentiell mit der Spannung			Die Elektronen des Halbleiters haben keine Probleme in das Metall überzutreten; der entgegengesetzte Strom wird auf Null fallen.
		Der Rückwärtsstrom vom Metall in den Halbleiter bleibt unverändert; aus Sicht des Metalls hat sich ja nichts geändert.			Stromfluß ist aus Sicht des Kontakts fast unbegrenzt möglich; letztlich werden die ohmschen Widerstände begrenzend wirken.
		Die Situation ist ziemlich ähnlich zum Vorwärtsbetrieb eines pn-Übergangs			Im wesentlichen "sehen" wir in diesem Ast der Kennlinie einen (kleinen) ohmschen Widerstand
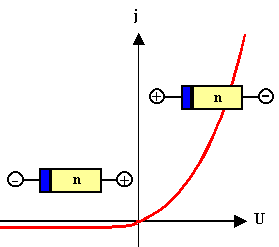
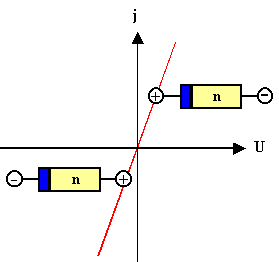
		In Summe erhalten wir eine Diodenkennlinie. Wir nennen diese Sorte eines Halbleiter-Metall Kontakts einen Schottky Kontakt oder - in der technischen Ausführung - eine Schottky Diode			In Summe erhalten wir die Kennlinie eines Ohmschen Widerstands oder einen Ohmschen Kontakt

	Wow!!! Eine kleine Zufälligkeit - die Austrittsarbeit ist ein bißchen größer oder kleiner - und schon ist das elektronische Verhalten des Metall-Halbleiter Kontakts grundverschieden.
		Und nochmal: Wow!!! Konstruiere das Banddiagramm nach relativ einfachen Regeln - und wir wissen, wie das Verhalten sein wird.
		Jedoch: Während die Vorhersage "Schottky" oder "Ohm" noch einfach zu machen ist, gilt das nicht mehr so ganz für die Formel der Kennlinie.
	Wer die Herleitung der pn-Kontakt Kennlinie verinnerlicht hat, wird keine großen Probleme haben, sich eine Formel für Schottky Kontakte herzuleiten. Für Ohmsche Kontakte ist es hoffnungslos, da hier Bahnwiderstände, und damit geometrische Faktoren dominieren.
		Wir wollen das hier aber nicht tun, sondern nur noch kurz weitere Aspekte der Halbleiter-Metall Kontakte behandeln.
	Die erste Frage ist natürlich nach den beiden anderen der vier Fälle: Wir starten mit p-dotierten Halbleitern
		Das ist zunächst eine sehr anspruchsvolle Übungsaufgabe. Anspruchsvoll, weil wir nun Löcher im Halbleiter mit Elektronen im Metall in Beziehung setzen müssen - es gibt keine Löcher im Metall. Aber man kann sich sehr gut selbst testen, wie weit man die Konstruktion von Banddiagrammen verstanden hat.
		Auch wer diese Übung nicht machen will, sollte sich unbedingt per direktem Link das Ergebnis anschauen!
		Übung 6.3-1 Schottky Kontakt mit p-Halbleiter

	Was man erhält ist in der nun erweiterten Ausgangstabelle festgehalten:
		Halbleiter (HL) Fermienergie Metall relativ zum HL im Banddiagramm Austrittsarbeit W Typ n-Typ Höher WHL < WMe Schottky Niedriger WHL > WMe Ohmsch p-Typ Höher WHL < WMe Ohmsch Niedriger WHL > WMe Schottky
	Das läßt sich am besten graphisch darstellen:
	Ein Metall, das zu n-Si einen Ohmschen Kontakt macht, wird also automatisch mit p-Si einen Schottky Kontakt produzieren und umgekehrt. Bei einem Metall, das zu einer Sorte HL einen Schottky Kontakt macht, muss man ein bißchen genauer hinschauen.
		Das ist von überragender technischer Bedeutung! Denn ohne Schottky Kontakte würde zwar ein kleiner Teil der Elektronikindustrie Schwierigkeiten haben, aber ohne Ohmsche Kontakte wäre die ganze Industrie schlicht nicht möglich
		Die Herstellung "guter" ohmscher Kontakte ist ein wichtiges, und durchaus schwieriges Thema der Halbleiterelektronik. Wir wollen deshalb ganz kurz die Praxis der Halbleiter-Metall Kontakte beleuchten
	Was bedeutet das in der Praxis?
		Einfach: Für ohmsche Kontakte zu p-Si oder generell zu p-Halbleiter nehmen wir Metalle mit großer Austrittsarbeit, d.h. Metalle die ihre Elektronen ungern hergeben. Das sind natürlich in erster Linie Edelmetalle, die uns auch sonst ganz lieb sind weil sie im Betrieb nicht "wegrosten".
		Bei n-Si oder generell n-Halbleitern haben wir ein Problem. Am besten wären Materialien, die Elektronenüberschuss haben, d.h. relativ leicht ein Elektron hergeben. Also die Alkali- oder Erdalkalimetalle (die kleinste Austrittsarbeit überhaupt hat Cs). Aus (hoffentlich) offensichtlichen Gründen sind diese Materialien aber nicht so toll für Anwendungen. Also schauen wir mal auf's Periodensystem mit eingetragenen Austrittsarbeiten:
		OK - wir haben ein Problem. In der Realität werden tatsächlich Kontakte aus z. B. Ba oder Ca verwendet - mit erheblichen techischen Problemen. Aber das wird uns in einer anderen Vorlesung beschäftigen.

	Halbleiter-Metall Kontakte in der Praxis
	Wir nehmen einen Halbleiter, verpassen ihm eine "perfekte" (= hochpolierte defektfreie) Oberfläche, reinigen sie sorgfältig und bringen dann eine Metallschicht auf.
		Dazu gibt es eine ganze Reihe von Verfahren, z.B. "Aufdampfen", die uns hier aber nicht weiter interessieren sollen.
		Dann messen wir die Kennlinie.
	Führt man diesen Versuch real aus, läuft man in eine ganze Reihe von Problemen:
	1. Wir brauchen auf der anderen Seite des Halbleiters einen richtig guten ohmschen Halbleiter-Metall Kontakt damit wir den Meßkreis schließen können. Falls das nicht sicher gestellt ist, wissen wir gar nicht, welchen der immer erforderlichen beiden Kontakte wir eigentlich messen.
		Eine typische Lösung dieses Problems besteht darin, die Rückseite extrem hoch zu dotieren. Damit wird jede Raumladunsgzone so dünn, daß die Ladungsträger im Zweifelsfall durchtunneln können. In anderen Worten: Selbst wenn der Kontakt eigentlich sperren sollte, wird er es nicht tun.
	2. Das Ergebnis der Messung wird fast nie mit der Theorie übereinstimmen - weder quantitativ, noch qualitativ. Egal wie die Austrittsarbeiten sich vergleichen, wir werden fast immer ein mehr oder weniger ausgeprägtes Diodenverhalten bekommen - auch wenn ganz klar Ohmsches Verhalten angesagt ist.
		Der Grund dafür ist, daß wir keinen Halbleiter-Metall Kontakt haben, sondern einen Halbleiter-Halbleiteroxid/Dreck-Metall Kontakt - wie beim naiven pn-Übergang.
		Man muß schon im Ultrahochvakuum (normales Hochvakuum genügt nicht) irgendwie die Oberflache in situ reinigen, um eine "nackte" Halbleiteroberfläche zu bekommen, sonst ist sie immer mit Oxid oder sonst was bedeckt.
	3. Wenn man das tut, und dann in situ das gewünschte Metall aufbringt, wird die Kennlinie immer noch nicht der Theorie folgen.
		Denn fast alle Hableitermaterialien sind chemisch sehr reaktiv - sie sind immer nur durch ihren Oxidüberzug geschützt. Bringt man ein Metall in unmittelbaren Kontakt mit z.B. Silizium wird sich sofort ein Silizid, eine Silzium-Metall Verbindung bilden. Die Reaktion wird bei Raumtemperatur zwar schnell zum Erliegen kommen (mangels Diffusion), aber wir haben zumindest eine dünne Silizidschicht - z.B. PtSi, Ni2Si oder PdSi2.
		Damit messen wir die Eigenschaften des Kontakts Silizium-Silizid-Metall. Da die Silizide ganz andere Eigenschaften haben als das beteiligte Metall (das gilt insbesondere auch für die Austrittsarbeit), kann man nicht erwarten, daß das Experiment die Vorhersagen der Theorie wiedergibt.
	Erst wenn wir die Theorie eines Silizium-Silizid Kontaktes mit der Messung eines solchen (aufwendig hergestellten) Kontakts vergleichen, finden wir eine gute Übereinstimmung.
		Man sollte sich aber davor hüten, das nur als Problem zu sehen! Im Gegenteil - es eröffnet spannende Möglichkeiten sich diodenartige Kontakte zu generieren, die es "eigentlich" gar nicht geben sollte. Solange die Resultate verläßlich und reproduzierbar sind, wird sich der Praktiker nur am Rande dafür interessieren, was genau die Theorie dazu sagt.
		Fragebogen / Questionaire Multiple Choice Fragen zu 6.1.3

© H. Föll (MaWi 2 Skript)