 |
Die Eigenschaften des Halbleiter-Metall Kontakts definieren sich, wie wir inzwischen
gelernt haben, weitgehend aus dem Banddiagramm. |
|
 |
Die Konstruktion des Banddiagramms ist jetzt relativ problemlos - wir verwenden
unser altes Rezept. Einige zusätzlich notwendige Spezialitäten diskutieren
wir sobald sie auftauchen. |
|
 |
Wir brauchen die Fermienergie des jeweiligen Metalls. Das ist aber nichts anderes als die
Austrittsarbeit
W; wir gehen davon aus, daß sie bekannt ist. |
|
 |
Wir müssen uns allerdings für eine der vier
möglichen Varianten entscheiden: |
|
|
| Halbleiter (HL) |
Fermienergie Metall
relativ zum HL im Banddiagramm |
Austrittsarbeit W | | n-Typ | Höher |
WHL < WMe | | Niedriger | WHL > WMe |
| p-Typ | Höher | WHL < WMe |
| Niedriger | WHL > WMe |
|
|
 |
Die Spalte mit den Austrittsarbeiten
erinnert auch daran, daß eine Fermienergie, die im Banddiagramm "höher" liegt, eine kleinere Austrittsarbeit
hat, da die absolute Energieskala mit Nullpunkt "im Unendlichen"
von oben nach unten läuft. |
 |
Warum diese Fallunterscheidungen sinnvoll sind, werden wir sehen, sobald wir die
Konstruktion versuchen. |
|
 |
Das Banddiagramm des Halbleiters kennen wir, das Banddiagramm eines Metalls eigentlich
nicht. Uneigentlich aber schon - es ist einfach ein bis
zur Fermikante gefülltes Kontinuum. |
|
 |
Wir behandeln mal die beiden Fälle zum n-Typ Halbleiter parallel,
exakt so wie wir es beim pn-Übergang gemacht haben. Wir müssen
aber einen Punkt "0" vorschalten: Die Ausgangssituation hat sich geändert! |
 |
Wir haben jetzt einen "Hetero"kontakt
(im Gegensatz zu dem bisher behandelten Si - Si "Homo"kontakt.
|
|
 |
Es gibt also nicht mehr auf beiden Seiten eine im Material immanent vorhandene
Referenzenergie, z.B. die Valenz- oder Leitungsbandkante, die wir als Nullpunkt oder auch nur als gemeinsamer Referenzpunkt
der Energieskala auf beiden Seiten benutzen können. |
|
 |
Wir müssen jetzt eine gemeinsame Referenzenergie, einen Energienullpunkt
zusätzlich einführen. Das ist die Vakuumenergie,
d.h. die Energie die ein aus dem Material entferntes Elektron im "Unendlichen" haben wird; sie ist per definitionem
= 0. |
 |
Damit können wir jetzt versuchen, die Banddiagramme für die beiden möglichen
Fälle paralle zu konstruieren. |
|
| |
| | |
WHL < WMe |
WHL > WMe |
| | |
| |
 |
0. Ausgangssituation |
|
|
|
 |
Die Vakuumenergie ist jetzt auch eingezeichnet,
um die Austrittsarbeiten verdeutlichen zu können. Die von Elektronen besetzten Zustände sind lindgrün markiert |
|
 |
Was beim Kontakt geschehen wird ist klar: Links werden (netto) Elektronen vom Halbleiter ins
Metall wandern und das Metall negativ aufladen, rechts ist es genau umgekehrt. |
| | |
|
|
| | |
|
 |
1.
Zeichne die Fermienenergie als horizontale Linie; markiere den Kontakt |
|
|
 |
2.
Zeichne "weit" links vom Kontakt das Banddiagramm von Material 1; weit rechts
das von Material 2; immer relativ zu der bereits festgelegten Fermienergie. |
|
 |
Unvermeidliche Konsequenz: Die Nullpunktslinie muß eine Kinke bekommen!
Etwas seltsam - aber klar!?? |
 |
Nein? Dann den Link
betätigen! |
|
 |
Hier nur soviel: Gleichgewicht für das System mit
vielen Elektronen wird in Banddiagrammen charakterisiert durch ein fiktives
Elektron mit einer überall konstanten Fermienergie. |
|
 |
Betrachtet man aber einen energetisch Null ergebenden Kreisprozeß für ein reales Elektron, läßt sich das nicht ohne eine gewisse Inkonsistenz, eben eine
"Kinke" in der Energienulllinie, in ein- und derselben Zeichnung darstellen. |
|
 |
Das hat aber keine Bedeutung; wir haben nur ein weiteres Beispiel, dass hochverdichtete abstrakte
Schemata gegentlich an Grenze stoßen. |
|
| | |
|
|
| | |
| |
 |
3.
Verbinde Leitungs- und Valenzband durch eine "gefühlsmäßig" gezeichnete
Bandverbiegung. |
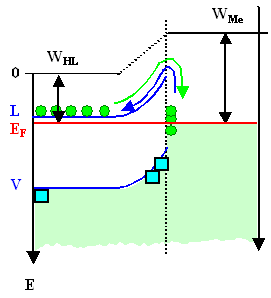 |
| Raumladungszone |
|
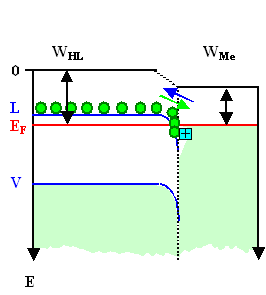 |
| Akkumulation - neu! |
|
|
 |
Ein erstes Problem taucht auf: Es gibt kein Leitungs- und Valenzband auf der anderen Seite.
Was wird verbunden? |
|
 |
In diesem Fall gilt: Verbinde korrespondierende Zustände für Elektronen (und oder
Löcher). Auf jeden Fall müssen wir eine Bandverbiegung im Halbleiter konstruieren, der für Elektronen wie
ein Potentialberg der Höhe DEF wirkt; denn es gilt das Gleichgewichtsprinzip: Ein Elektron gewinnt keine Energie mehr durch einen Übergang vom
Halbleiter ins Metall (links) bzw. vom Metall in den Halbleiter (rechts). |
|
 |
Warum keinen Potentialberg im Metall? Im Prinzip sollte (und wird) auch im Metall ein Potential"gefälle"
sein. Aber die "Dicke" (= Debye Länge)
ist immer so klein, dass diese Potentialbarriere kein Rolle spielt; die Ladungsträger tunneln
einfach durch. |
| |
| |
|
 |
Falls das Gefühl immer noch nicht reicht: Wir wissen immer,
auf welcher Seite die Elektronen zurückgedrängt oder "angezogen" werden. Das Band muß dann immer
so gebogen werden, daß der Abstand Fermienergie - Leitungsbandkante sich entsprechend vergrößert oder verkleinert.
|
|
 |
Wir haben auch "Vorwärts"- und "Rückwärts"ströme
(grüne und blaue Pfeile), die notgedrungen betragsmäßig gleichgroß sein müssen. Wir wissen bloß
nicht so recht, welche Farbe vorwärts bzw. rückwärts symbolisiert. |
|
 |
Die jeweiligen Ladungsüberschüsse sind angedeutet: Links eine Flächenladung
von Elektronen auf der Metallseite (die Gegenladungen der positiv ionisierten Donatoren sind aus Gründen der Übersichtlichkeit
nicht eingezeichnet); rechts eine positve Flächenladung auf der Metallseite und eine Anhäufung von Elektronen
auf der Halbleiterseite. |
| |
|
 |
Im linken Fall bildet sich also eine Raumladungszone wie
gehabt, im rechten Fall aber haben wir etwas neues; das wir kurz besprechen müssen |
| | |
| |
|
Akkumulation als neues Phänomen |
| | |
 |
Wir haben offensichtlich die Dichte der Majoritätsladungsträger lokal erhöht. Das ist neu - bisher wurde sie durch Kontakte immer nur erniedrigt. |
|
 |
Es gibt aber keinen Grund, warum das nicht auch passieren kann. Die Fermienergie
liegt jetzt sogar für ein kurzes Stückchen im Leitungsband - auch dagegen spricht vom Grundsatz her nichts. |
|
 |
Obwohl das ein prinzipiell völlig normales Verhalten ist, spricht man in solchen Fällen
von "entarteten Halbleitern"
(engl. "degeneration"). |
 |
Eine Entartung kann auf mannigfaltige Weise erreicht werden. Im Gleichgewicht
zum Beispiel durch |
|
 |
Sehr hohe Dotierung. |
|
 |
Kontakte, die so gebaut und/oder vorgespannt sind, daß sie die Majoritätsladungsträger
anziehen und damit am Kontakt anreichern - wie im obigen rechten Fall. Man spricht dann von Anreicherung
oder Akkumulation. |
 |
Man kann Akkumulation aber auch im Nichtgleichgewicht erreichen.
|
|
 |
Das scheint zwar ein Widerspruch in sich zu sein, denn in Nichtgleichgewicht ist die Fermienergie
eigentlich gar nicht definiert; Aussagen über ihre Lage sind dann im Prinzip sinnlos. Ladungsträgerkonzentrationen
sind aber immer definiert, und man kann sich natürlich die Frage stellen: Wo müßte die Fermienergie liegen,
wenn für die vorliegenden Ladunsgträgerkonzentrationen Gleichgewicht herrschen würde? |
|
 |
Was herauskommt nennt man "Quasifermienergie".
Das ist nicht nur eine sehr sinnvolle Größe, sondern sie kann auch im Leitungs- oder Valenzband des Halbleiters
liegen und damit Entartung signalisieren. |
|
 |
Machbar ist Entartung in diesem Fall insbesondere, indem man über z.B. über einen
pn-Kontakt Unmengen an Ladungssträger in die jeweils ander Seite injiziert. Jeder Halbleiterlaser
beruht auf diesem Prinzip; Entartung im Nichtgleichgewicht ist die absolut notwendige Bedingung für sein Funktionieren |
 |
Noch etwas unklar ist die Ausdehnung der Akkumulationszone. Aber im Grunde sind
wir schon einmal auf eine ähnliche Fragestellung gestoßen
- sie wurde in einem eigenen Modul behandelt. |
|
 |
Die Ausdehnung der Akkumulationszone ist identisch mit der Eindringtiefe eines externen elektrischen
Feld in ein Material. Und jedes Feld wird solange in ein Material eindringen, bis jede Feldlinie eine Ladung gefunden hat,
auf der sie enden kann. |
|
 |
Betrachten wir zum Beispiel ein Metall, dann gibt es entweder sehr viele Elektronen, oder,
falls ich die Elektronen nur ein ganz kleines bißchen zurückdränge, sehr viele positiv geladene Metallionen,
die jedes Feld auf kürzeste Distanz "absorbieren" oder abschirmen können. Die Dicke dieser "Abschirmschicht"
heißt Debyelänge; Details dazu finden sich in in anderen
Hyperskripten. |
 |
In dotierten Halbleitern (und nur in dotierten
Halbleitern), muß die Lage differenziert gesehen werden. Für eine Polarität
der Feldes wird die Abschirmung durch die beweglichen Majoritätsladungsträger übernommen werden können.
Es sind viele, und sie sind beweglich; sie können sich also in Grenzflächennähe
anhäufen (= akkumulieren) - die Debyelänge ist entsprechend klein. |
|
 |
Polt man das Feld um, muß es jetzt von den unbeweglichen ionisierten Dotieratomen abgefangen
werden. Sie sind nicht beweglich, ihre Dichte ist viel kleiner als die der positiv geladenen Metallionenrümpfe, und
man muß schon eine größere Zone - eben die Raumladungszone - von den beweglichen Majoritätsladungsträgern
freiräumen, um genügend Dotieratome zu "entblößen", die das Feld abschirmen können.
Die Debyelänge ist größer als im umgekehrten Fall - nur daß man sie nicht mehr Debyelänge nennt,
sonder Raumladungszonenweite. |
|
 |
Offenbar nimmt die Debyelänge mit der Konzentraion an verfügbaren Ladunsgträgern
ab - in Metallen ist sie typischerweise < 1 nm - man sagt "elektrische Felder können in Metalle nicht
eindringen". In Isolatoren geht sie gegen ¥, und in (dotierten) Halbleitern
ist sie nicht besonders groß, aber doch deutlich größer als in Metallen. Auch dazu haben wir schon mal
einen "advanced" Modul bemüht. |
 |
Langer Rede kurzer Sinn: Das bißchen Bandverbiegung, das in rechten Fall
noch eingezeichnet ist, symbolisiert jetzt die Debyelänge; sie ist auf jeden Fall viel kleiner als die Raumladungszonenweite. |
 |
So weit so gut. Die Frage ist jetzt natürlich: Was passiert, wenn wir eine
externe Spannung anlegen. Dieser Frage werden wir im nächsten Unterkapitel nachgehen |
| |
|
© H. Föll (MaWi 2 Skript)