"Dielektrika" in einem Kondensator

	Wir betrachten der Reihe nach, was geschieht wenn wir in eine Plattenkondensator mit elektrisch isolierten Platten einen Leiter, einen Isolator und einen Halbleiter einbringen. Dies wird uns fast zwanglos auf einen Schlüsselbegriff der Halbleiterei bringen.
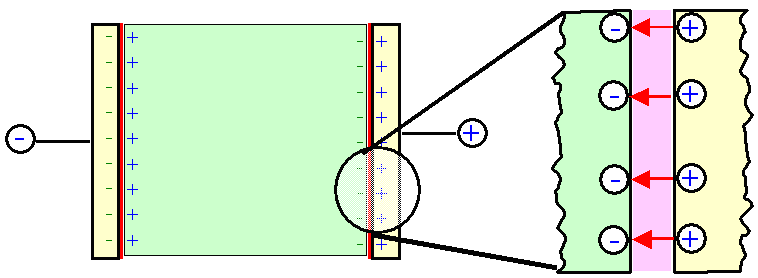
		Wir beginnen mit einem Leiter. Falls wir ein leitendes Material einfach "nur so" zwischen zwei Kondensatorplatten stecken, haben wir natürlich eine elektrischen Kurzschluß, deshalb spendieren wir noch zwei (im Grenzfall unendloch dünne) Isolatorschichten. Die Geometrie und die Ladungsanordnung sieht dann so aus:
		Von den vielen beweglichen Elektronen werden sich soviele an die rechte Leiteroberfläche begeben, bis jede positive Ladung auf der Kondensatorplatte ein Elektron unmittelbar gegenübersitzen hat. Die Ladungsdoppelschicht ist nur durch die Dicke der isolierenden Schicht getrennt.
	Es ist am einfachsten, sich das elektrische Feld mit Feldlinien zu vergegenwärtigen, und dabei den folgenden Fundamentalsatz zu beachten: Feldlinien beginnen und enden an Ladungen.
		Die Lage ist dann einfach: An jeder positiven Ladung der Kondensatorplatte beginnt eine Feldlinie; sie endet an dem gegenübersitzenden Elektron. Auf der andern Seite sind die Dinge genau umgekehrt. Die Feldlinien gehen von den positiven Ionerümpfen aus, die übrigbleiben wenn sich die Elektronen etwas wegbewegen
		Das Innere des Leiter ist feldfrei - wir haben keine Feldlinien, und damit auch kein Feld.

Metalle zwischen den Kondensatorplatten

	Betrachten wir die Situation nun mit Hilfe der Poisson-Gleichung. Ausgangspunkt ist immer die (Netto)ladungsdichte.
		Einmalige Integration führt dann zur Feldstärke, nochmalige Integration zum elektrischen Potential.
		Das ist qualitativ leicht zu machen; wir erhalten nebenstehendes Diagramm.
		Die Ladungsdichte ist schlicht als Rechteck wiedergegeben; im Extremfall "endlich guter Leiter" wären es Delta Funktionen
		Die Feldstärke folgt durch einmalige Integration (= Fläche unter Ladungskurven). Sie ist konstant und maximal zwischen den Dipolschichten; im Inneren des Metals ist sie Null - wie es sein muß.
		Das (aus zeichentechnischen Gründen negative) Potential folgt aus der Integration der Feldstärke.Es steigt über die Dipolschichten, bleibt im Inneren des Metalls konstant, und steigt dann auf den Endwert.
		Auch das ist leicht zu verstehen; man muß sich ja nur klarmachen, welche Arbeit an einer Probeladung verrichtet wird, die z.B. von links nach rechts geführt wird. Beim Durchlaufen der ersten Dipolschicht wird kräftig Energie gewonnen, die dann konstant bleibt; in der zweiten Dipolschicht wiederholt sich die Chose.
	Es reicht völlig aus, wenn sich die Gesamtheit der freien Elektronen gegenüber den Atomrümpfen um ein Kleines in Richtung des positiven Pols verschiebt. Ein Atomdurchmesser Verschiebung produziert sofort eine Flächenladungsdichte von etwa einer Elementarladung pro Gitterkonstantenquadrat - und das ist sehr viel
		Am Rande notieren wir noch: Aus dem ohne Metall wohldefinierten Kondensator mit einer endlichen Kapazität sind mit Metall zwei hintereinander geschaltete Kondensatoren geworden, deren Kapazität mit auf Nulll strebende Dicke der Isolatoroschicht gegen ¥ strebt.
		Damit können wir einem Metall formal eine Dielektrizitätskonstate von eMetall = ¥ zuschreiben

Isolatoren zwischen den Kondensatorplatten

	Was erhalten wir nun für ein Dielektrikum?
		Es gibt keine beweglichen Ladungen. Bestenfalls werden ein paar Dipole induziert, oder es drehen sich bereits vorhandene Dipole in Feldrichtung. Näheres ist im Hyperscript "Electronic Materials" nachzulesen.
		Hier halten wir nur fest, daß die letzte Schicht Dipole auf der Oberfläche des Dielektrikums eine flächenhafte Restladung übrigläßt, die je nach Dielektrizitätskonstante mehr oder weniger groß ist. Niemals jedoch so groß wie die Ladung auf der Kondensatorplatte!
		Damit ist das Innere des Dielektrikums nicht feldfrei.
		Die zweimalige Integration der Ladungsdichteverteilung ergibt schematisch das nebenstehende Bild.

Halbleiter zwischen den Kondensatorplatten

	Was ist beim Halbleiter nun anders als bei Metallen und Isolatoren?
		Es gibt zwar bewegliche Ladungen, aber viel weniger als in Metallen.
		Um die der Plattenladung entsprechende Flächenladung an das Ende des Materials zu bringen, muß die Konzentration der Ladungsträger in der Nähe von x = 0 und x = L sehr viel höher werden als im Volumen.
		Das ist bei Metallen anders: Hier reicht eine leichte Überhöhung der Gleichgewichtskonzentration immer aus.
		Damit bekommen wir vom Materialende in Richtung Materialinneres einen sehr großen Konzentrationsgradienten - und große Konzentrationsgradienten treiben große Diffusionsströme, die versuchen den Gradienten abzubauen.
		In einem dynamischen Gleichgewicht zwischen elektrischen Kräften, die die Ladungsträger ans Materialende treiben, und den Diffusionsströme, die die Ladungen zurücktreiben, stellt sich eine Ladungsträgerverteilung ein, die etwa so aussieht wie nebenstehend angedeutet.
		Die Integration der Ladungdichteverteilung ist qualitativ einfach und im Bild angedeutet.
		Das elektrische Feld dringt also etwas in das Material ein, die typische Eindringtiefe heißt Debyelänge dDebye.
	Die Debyelänge ist eine universelle Materialkonstante, die nicht nur der Halbleiterphysik, sondern z.B auch in der Ionik eine entscheidende Rolle spielt.
		Wir können dem Halbleiter jetzt auch eine Dielektrizitätskonstante zuschreiben, die nicht mehr wie bei Metallen = ¥ ist.
		Aber so ganz klar ist hier noch nicht , wie groß eHalbleiter sein wird.
	Im Grunde beschreiben wir hier den allgemeinen Fall: Leiter und Isolatoren sind schlicht Spezialfälle mit einer Debyelänge von nahe Null bzw. Unendlich. Allgemein gilt für die Debyelänge
		d  =  Debye Länge  =  æ ç è ee · 0 kT e2 · n ö ÷ ø 1/2
		Die Debyelänge ist damit nur eine Funktion der Dichte n der beweglichen Ladungsträger und der Dielektrizitätskonstante e.
		Mehr dazu im Hyperskript "Electronic Materials" und im Hyperskript "Semiconductors".

Mit Frame

6.1.3 Bandverbiegung und Raumladungszone

6.3.1 Bandstruktur des Halbleiter-Metall Kontakts

6.4.3 MOS Transistoren

Bandverbiegung im "Kondensator"

© H. Föll (MaWi 2 Skript)