|
Um die genaue Form der Bandverbiegung berechnen
zu können, tun wir gut daran, uns die Situation ausnahmsweise mal nicht im Banddiagramm, sondern im gewöhnlichen
Ortsraum anzuschauen. |
|
 |
Berechnen heißt, die Poissongleichung,
in der die Ladungsdichte mit dem elektrischen Potential verknüpft wird, für den betrachteten Fall zu lösen. |
|
 |
Dazu müssen wir erstmal wissen, wo sich die diversen Ladungen befinden. |
| |
|
 |
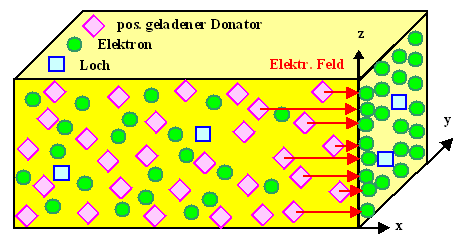
Die beweglichen Elektronen sind in Oberflächennähe zurückgedrängt
(soweit die Bandverbiegung eben reicht), die wenigen Löcher können wir vergessen - aber was immer
bleibt, sind die ortsfesten Dotieratome, in unserem Fall positiv geladene ionisierte Donatoren. |
|
 |
Offenbar sind diese ortsfesten positiven Ladungen die Partner der in die Oberfläche gewanderten
ehemaligen Volumenelektronen: Von ihnen gehen die Feldlinien aus,
die auf den negativen Ladungen der Oberfläche enden. |
|
 |
Im Bereich der Bandverbiegung haben wir also noch eine feste, zeitlich unveränderliche
Verteilung von Ladungen im Raum, wir nennen das ganz Gebilde von nun an Raumladungszone
RLZ (engl.. Space Charge Region; SRC). Die Raumladungszone ist ein fundamentaler
Begriff der Halbleitertechnologie; der in den elementaren Wortschatz gehört. |
 |
Die Ausdehnung oder Breite dRLZ der Raumladungszone (=Ausdehnung
der Bandverbiegung) ist also letztlich dadurch bestimmt, wie weit man ins Innere des Materials gehen muß, bis man
genügend positive geladenen Donatorionen gefunden hat, um die negativen Oberflächenladungen zu kompensieren. |
|
 |
Es ist also jetzt schon klar, daß in nur leicht dotierten Halbleitern
(=wenig Dotieratome) die Raumladungszone breiter sein muß, als in stark dotierten. |
 |
Die Ausdehnung oder Breite
dRLZ der Raumladungszone läßt sich auf zwei Arten
berechen |
|
 |
1. Wir lösen die zugehörige Poisson Gleichung. Das werden wir auch - aber noch nicht sofort. |
|
 |
2. Wir denken scharf nach und greifen
auf etwas zurück, das wir bereits kennen. Das werden wir als erstes versuchen. |
 |
Was wir bereits kennen, ist ein Plattenkondensator:
Zwei Platten mit der Fläche F im Abstand d enthalten die Ladung ±Q;
dazwischen ist noch ein nichtleitendes Material mit der Dielektrizitätskonstaten er
. Der Kondensator hat die Kapazität C, gegeben durch |
| |
|
|
 |
Dabei ist e0 die dielektrische Suszeptibilität des Vakuums. Zwischen den Platten ist dann ein elektrisches
Feld E=-dU/dx; U ist die anliegende Spannung |
 |
??? - was nützt das? Nun ja - das Bild oben
zeigt bei genauer Betrachtung eine Anordnung, die ziemlich viel Ähnlichkeiten mit einem Plattenkondensator aufweist. |
|
 |
- Rechts ist negative Ladung auf einer dünnen "Platte".
- Links ist positive Ladung; allerdings nicht auf einer Platte, sondern "verschmiert". Das entpricht einer "Verschmierung"
des Abstands d der Platten zwischen d=0 und d=dRLZ; eine Platte
ist sozusagen aus Wellblech.
- Zwischen den "Platten" ist ein Material, das nur sehr schlecht leitet - denn in der RLZ gibt es kaum
freie Ladungsträger.
- Im Material zwischen den "Platten" ist ein elektrisches Feld.
|
|
 |
Mit ein bißchen Nachdenken erkennt man also: Eine Raumladungszone ist einem Kondensator
nicht nur ähnlich - sie ist ein Kondensator, oder allgemeiner
gesagt, sie hat eine in Farad meßbare Kapazität. |
 |
Das einzige Problem ist der "verschmierte" Plattenabstand. Wir trauen
uns einfach mal und beschließen: In so einem Fall nehmen wir einfach einen mittleren
Plattenabstand <d>=½ · dRLZ. |
|
 |
Für die Kapazität unseres RLZ-Kondensators haben wir jetzt zwei Gleichungen: |
| |
| CRLZ |
= |
2 · eSi · e0
· F
dRLZ |
|
| CRLZ |
= | Q
UK | = |
Q
DEF/e | = |
e · (ND · F · dRLZ)
DEF/e | = |
e2 · (ND · F · dRLZ)
DEF |
|
|
 |
Die 1.
Gleichung ist klar, die 2. bis nach dem ersten Gleichheitszeichen auch. Was danach kommt, muß vielleicht
erklärt werden: |
 |
1. Wir kennen die an unserem Raumladungskondensator
anliegende Spannung U, hier genauer mit UK=Kontaktspannung bezeichnet.
|
|
 |
Denn die Spannung zwischen zwei Punkten ist die Differenz
des elektrostatischen Potentials der beiden Punkte, und damit der Unterschied in der
elektrostastischen Energie dividiert durch die Ladung (=e in unserem Fall).
|
|
 |
Der Unterschied in der elektrostastischen Energie ist aber gerade der Unterschied der Fermienergien
vor dem Kontakt (=DEF), denn genau um diesen Betrag haben wir ja die
Energieachsen verschoben. Damit gilt UK=DEF/e.
|
 |
2. Wieviele Ladungen Q haben wir auf unseren "Platten"?
|
|
 |
Von den negativen Ladung auf der Oberfläche wissen wir es nicht, aber von den positiven
Ladungen in der Raumladungszone wissen wir es schon: Es sind genau so viele Elementarladungen, wie wir ionisierte Dotieratome
in der RLZ haben. |
|
 |
Falls alle Dotieratome ionisiert sind (wovon wir jetzt
ja immer ausgehen), braucht man also nur die Dichte
ND mit dem Volumen F · dRLZ der Raumladungszone zu multiplizieren,
um die Zahl der in der RLZ enthaltenen ionisierten Dotieratome zu erhalten; damit es eine Ladung wird muß noch
mit e multipliziert werden. |
 |
Was wir jetzt im Kasten oben haben sind 2 Gleichungen für die 2
Unbekannten CRLZ und dRLZ. |
|
 |
Die Lösung ist beliebig einfach, wir erhalten |
| |
| dRLZ |
= |
æ
ç
è |
2 · er · e0
· DEF
e2·ND
| ö
÷
ø |
½ |
| CRLZ /F |
= |
æ
ç
è
|
2 · er · e0
· e2 ·ND
DEF
| ö
÷
ø |
½ |
|
|
|
 |
Das war nicht so schwer! Und wir haben eine relativ einfache Formel für die
Weite der RLZ erhalten. |
|
 |
Wie vorhergesagt, nimmt dRLZ zu,
wenn die Dotierkonzentration abnimmt - mit (1/ND)1/2, um genau zu sein. |
|
 |
Weiterhin nimmt dRLZ zu, wenn die Differenz der Fermienergien größer
wird - auch das ist klar. |
 |
Allerdings stehen zwei Fragen im Raum. Erst die einfachere der beiden: |
|
 |
Frage 1: Stimmt das überhaupt? Immerhin haben wir
aus der RLZ nur durch Tricksen einen Plattenkondensator machen können. Oder anders herum gefragt: Wie gut ist
die Gleichsetzung des "mittleren" Abstands der Kondensatorplatten mit der halben RLZ Weite? |
|
 |
Antwort: Die Formel stimmt exakt! Das weiß "man"
(und wir gleich auch), aus der Lösung der Poissongleichung für diesen Fall - wir erhalten nämlich das gleiche
Ergebnis. |
|
 |
Frage 2: Was ist denn die Dielektrizitätskonstante
er von Si? Si ist ja schließlich ein Halbleiter und kein
Dielektrikum? |
|
 |
Antwort:
Jedem Material kann man eine Dielektrizitätskonstante zuschreiben - es ist nur
nicht immer sinnvoll, es in einen Kondensator zu stecken. Wir haben das in einem extra
Modul auch schon mal angesprochen. |
 |
Wir wollen uns das Leben aber nicht unnötig schwer machen, sondern uns zwei
Möglichkeiten zur eindeutigen Messung der Dielektrizitätskonstante eines beliebigen
Halbleiters überlegen: |
|
 |
1. Wir stecken das Material bei T=0 K in den Plattenkondensator. Dann
fließt garantiert kein Strom, da alle Halbleiter jetzt Isolatoren sind. Die Dielektrizitätskonstante ist eindeutig
meßbar; selbst wenn wir ein bißchen aufwärmen sollte es noch klappen; wir müssen nur zur Auswertung
der Messung dem "reinen" Kondensator den durch die beginnende Leitfähigkeit gebildeten Widerstand parallel
schalten und entsprechend berücksichtigen. |
|
 |
2. Wir erinneren uns,
daß alle Halbleiter für Licht mit h n
< EG vollständig durchsichtig sind - und dann einen Brechungsindex
nOpt haben, der (wie wir wissen sollten) durch folgende Gleichung gegeben wird: |
| |
| nOpt | = |
æ
è |
eHalbleiter |
ö
ø | 1/2 |
|
|
|
 |
Der Brechungsindex ist also nur eine etwas andere Form der (frequenzabhängigen) Dielektrizitätskonstante.
Spätestens damit läßt sich unser gesuchtes er auch bei hohen Temperaturen bestimmen.
|
 |
Was wir finden werden ist, daß Halbleiter typischerweise relativ große
Dielektrizitätskonstanten haben - sie liegen irgendwo zwischen 10 - 20. |
|
 |
Damit haben wir eigentlich die Raumladungszone - ihr Zustandekommen
und ihre Ausdehnung - schon ziemlich gut verstanden. Was noch fehlt ist die formale Berechunung und die genaue Form der Bandverbiegung. |
|
 |
Jetzt muß eben doch die Poisson Gleichung gelöst
werden. |
| |
|
| |
 |
Hier schauen wir uns nur an, wie die Lösung prinzipiell aussehen muß:
| |
|
|
 |
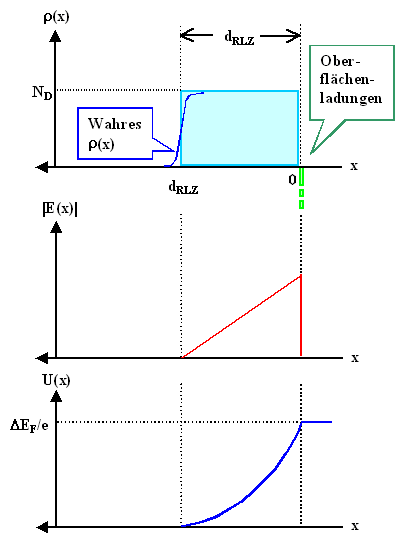
Wir haben in der RLZ eine konstante Ladungsdichte r(x, y, z)=ND; das ist durch das hellblaue Rechteck
angedeutet. Außerhalb der RLZ ist sie (im Halbleiter) =0. |
|
 |
Die negativen Ladungen auf der Oberfläche bilden eine Art Delta-Funktion (grün angedeutet);
wir brauchen sie hier aber erstmal nicht zu berücksichtigen. |
|
 |
Natürlich wird die Ladungsdichteverteilung nicht streng rechteckig sein sondern, wie
angedeutet, eine weiche Flanke haben. Aber auch das ignorieren wir erstmal, da es nur minimalen Einfluß auf die Lösungen
nimmt. |
 |
Zu lösen ist also die eindimensionale Differentialgleichung für eine
Ladungskonzentration ND zwischen x=0 und x=dRLZ |
|
|
|
|
|
|
|
| |
|
| |
|
|
 |
Dazu müssen wir nur zweimal integrieren. Die erste Integration liefert die Feldstärke; wir erhalten eine Gerade wie mit der roten Kurve qualitativ
angedeutet. Für die quantitativen Parameter müssen wir die Übungsaufgabe
machen | |
|
 |
Die zweite Integration liefert das elektrostatische
Potential oder die Kontaktspannung, falls wir das linke
Ende auf UK=0 setzen. Wir erhalten eine Parabel. Damit wäre
die Form der Bandverbiegung jetzt auch klar. |
|
|
|
 |
Zur quantitativen Berechnung braucht man zwei Randbedigungen. |
|
 |
Eine davon ist auch unmittelbar klar: Die gesamte Potentialdifferenz muß
DEF/e sein, denn das ist die Potentialverschiebung, die bei Gleichgewicht vorliegen
muß. Über die zweite denken wir selbst ein bißchen nach - auch sie ist in der Zeichnung enthalten. |
|
 |
Die Breite der Raumladungszone ergibt sich letztlich aus den Randbedingungen.
Qualitativ ist im rechten Bild zwar alles klar, aber um obige Formel zu erhalten muß man jetzt halt rechnen.
|
 |
Wie versprochen, haben wir aus unserem
etwas seltsamen Kontakt von Volumen und Oberfläche eine ganze Menge Honig gesaugt. Aber es ist noch mehr davon da! |
|
 |
Und darauf wollen wir schnell noch einen kurzen Blick werfen. |
| |
|
|
Volumen - Oberflächenkontakt
mit zusätzlicher externer Spannung |
| |
|
 |
Was passiert, wenn wir sowohl das Volumen, als auch die Oberfläche
mit einem ohmschem Kontakt versehen, und dann eine äußere
Spannung Uex anlegen? |
|
 |
Wie wir das tun, d.h. wie wir Volumen und
Oberfläche kontaktieren, müssen wir beim Gedankenversuch
nicht wissen. Um die Lage einfach zu machen, erden wir das Volumen (d.h. wir definieren
VVol=0), so daß nur an der Oberfläche die zusätzliche Spannung ±Uex
anliegt. Mit dem ± Zeichen soll angedeutet werden, dass man die gesamte Spannung vergrößern oder verkleinern
kann - je nach Vorzeichen der angelegten externen Spannung. |
|
 |
Je nach Vorzeichen der Spannung muss das Vorzeichen des Potentials gewählt
werden. Man kann die Konventionen auswendig lernen, oder sich schlicht daran halten, dass pos. Spannung die Elektronen "anzieht",
d.h. das Potential senkt. Das bedeutet, dass man in den nachfolgenden Formeln nur das – Zeichen braucht falls
man U mit Vorzeichen einsetzt; eine negative Spannung führt dann zum +. |
|
 |
Damit haben wir aber auch die zusätzliche elektrostatische Energie
– e ·Uex für die Elektronen. Und was das bedeutet wissen
wir schon: |
 |
Wir müssen das Banddiagramm der Oberfläche lokal um
den Betrag – e ·Uex verschieben; dazu müssen wir die Bänder zusätzlich
verbiegen |
|
 |
Solange kein Strom fließt ist alles wie gehabt, wir müssen nur
die externe Spannung
Uex zur Kontaktspannung
UK = – DEF/e addieren, um die
gesamte am Kontakt anliegende Spannung U zu erhalten : |
| |
|
|
 |
Je nach Vorzeichen von U wird also die insgesamt anliegende Spannung vergrößert
oder verkleinert. |
 |
Alle Formeln können beibehalten werden, wir müssen nur UK
durch U ersetzen und erhalten |
|
|
| dRLZ | =
| æ
ç
è
|
2 · eSi · e0·
(DEF – e ·Uex)
e2
· ND |
ö
÷
ø |
½ |
| CRLZ /F |
= |
æ
ç
è
|
2 · eSi · e0
· e2· ND
DEF – e · Uex |
ö
÷
ø |
½ |
|
|
|
 |
Das ist schon mal nicht schlecht! Wir könnten einen abstimmbaren
Kondensator bauen! Durch die Größe der anliegenden Gleichspannung kann man die Kapazität des
Kontakts ändern, und dann das Wechselspannungsverhalten gezielt einstellen, z.B. die Resonanzfrequenz eines Schwingkreises. |
|
 |
Aber halt! Leider nur im Gedankenversuch! Wir wollen aber nicht nur gedanklich Radio hören
und Fernsehn gucken, sondern real. Dazu müssen wir dann aber in den nächsten Unterkapiteln
reale Kontakte machen. |
 |
Es bleibt noch mindestens eine Frage, die sich jetzt wieder
mit Macht aufdrängen müßte: |
|
 |
Kann man die Kontaktspannung UK
messen - im Gedankenversuch natürlich! Wird ein Voltmeter an unseren ja bereits
vorhandenen Kontakten eine Spannung anzeigen? |
|
 |
Noch härter gefragt: Kann man mit der Kontaktspannung einen Strom durch einen externen
Widerstand treiben? Dann hätten wir ein Perpetuum mobile! |
 |
Damit ist die Antwort auf obige Fragen klar: Nein,
und nochmals nein! |
|
 |
Nur: Warum die Antwort nein sein muß, ohne den 1. Haupsatz zu bemühen,
ist nicht so recht klar. |
|
 |
Die Antwort findet sich in einem extra Modul.
Aber erst selbst nachdenken! Hinweis: Man kann Gedankenversuche auch überstrapazieren. |
 |
Wir wollen aber an dieser Stelle jetzt nicht mehr tiefer in die Materie eindringen,
sondern dies bei realen Kontakten tun, die wir tatsächlich herstellen und kontaktieren können, nicht nur im Gedankenversuch. |
| |
|
© H. Föll (MaWi 2 Skript)