 |
Es gibt viele verschiedene Arten von Kontakten; das elektrische Verhalten (Strom-Spannungskennlinie)
ist aber nicht unmittelbar klar. |
|
 |
Ein realer Kontakt ist i.d.R. viel komplizierter als ein idealer Kontakt. Ohne
besondere Vorsichtsmaßnahmen wird man deshalb nicht die Eigenschaften eines Metall - Halbleiterkontaktes messen, sondern
die Eigenschaften des Kontakts Metall - Zwischenschicht (Dreck und Reaktionsprodukte) - Halbleiter. |
|
 |
Das gilt insbesondere für den Kontakt p-Typ Halbleiter - n-Typ
Halbleiter. Die technische Realisierung des resultierenden pn-Übergangs ist recht komplex. |
 |
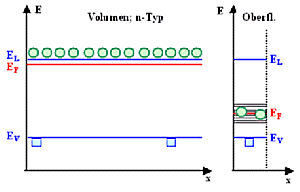
Die Oberfläche eines Kristalls kann aus guten Gründen als ein spezielles
Material betrachtet werden; der immer vorhandene "Kontakt" Halbleitervolumen - Halbleiteroberfläche ist ein
recht einfaches Modellsystem für einen allgemeinen Kontakt. |
|
 |
Die Oberfläche wird andere Zustände für Elektronen haben als das Volumen; insbesondere
sind viele Zustände in der Bandlücke zu erwarten, da nicht optimal abgesättigte Bindungen vorliegen. |
|
 |
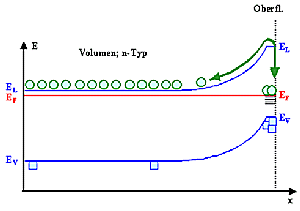
Dadurch wird die Fermienenergie in diesen Zuständen liegen, ziemlich unabhängig
von ihrer Lage im Volumen. Die Fermienergie wird durch viele Zustände in der Bandlücke "gepinnt". |
 |
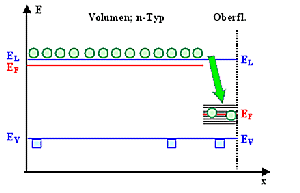
Beim gedanklichen Kontakt Volumen - Oberfläche werden Elektronen zu den energetisch
niedriger liegenden Zuständen der Oberfläche wandern; die Oberfläche wird dadurch so lange geladen, bis das
sich aufbauende elektrische Feld weiteren Energiegewinn kompensiert. Für Löcher gilt dasselbe, nur "anders
herum". |
|
 |
Im Banddiagramm sieht das dann so aus: |
| |
 |
 |
 |
| Vor Kontakt | Kontakt bei t = 0 |
Gleichgewicht |
|
 |
Als generellen Effekt bei allen Kontakten im Gleichgewicht
haben wir: |
|
 |
1. Konstante Fermienenergie überall.
2. Ladungsverschiebungen im Bereich der Grenzflächen.
3. Bandverbiegungen = Raumladungszonen = elektrische Felder im Bereich der Grenzflächen |
 |
Als generelles Rezept zur Erstellung von Banddiagrammen (im Ortsraum) haben wir |
| |
| 1. | Zeichne die Fermienenergie als horizontale Linie; markiere den Kontakt. |
| 2. |
Zeichne "weit" links vom Kontakt das Banddiagramm von Material 1; weit rechts das von Material 2; immer relativ
zu der bereits festgelegten Fermienergie. | | 3. |
Verbinde Leitungs- und Valenzband durch eine "gefühlsmäßig" gezeichnete Bandverbiegung. |
|
 |
Die Raumladungen in der Raumladungszone sind die ortsfesten geladenene Dotieratome;
auf der Oberflächenseite sind es die dort sitzenden Überschußelektronen |
|
 |
Die RLZ hat damit eine überschlagsmäßig über die Kondensatorformel
leicht zu errechnende Kapazität (pro Flächeneinheit); dadurch ist auch die Weite der Raumladungszone sehr leicht bestimmbar.
|
|
 |
Die quantitative Berechnung mit Hilfe der Poisson-Gleichung führt auf exakt dieselben
Formeln; bei Berücksichtigung einer zusätzlich angelegten externen Spannung ergibt sich |
| |
| dRLZ |
= |
æ
ç
è
|
2 · eSi · e0
· (DEF – e ·Uex)
e2 · ND |
ö
÷
ø |
½ |
| CRLZ /F |
= |
æ
ç
è
|
2 · eSi · e0
· e2 · ND
DEF – e · Uex |
ö
÷
ø |
½ |
|
|
|
 |
Danmit sind die wesentlichen Eigenschaften der RLZ zurückgeführt auf
|
|
 |
1. Die Grundeigenschaften der beiden Materialien (EF und er).
2. Technologieparameter (NDot und Uex). |
© H. Föll (MaWi 2 Skript)


