| | |
Radiocarbon (C14) Dating |
|
|
The Basics |
 |
Of course you know how radiocarbon or C14 dating works on principle. I did credit
you with a halfway decent education, remember? So in what follows I only want to refresh your memory. |
 |
The first thing to remember is that plants turn the carbon dioxide or CO2
contained in the air into solid organic stuff like barley (for making beer), leaves (for shading beer gardens), grass, cauliflower.
Or worse, leeks, celery, Brussels sprouts and all kinds of salad. Then your wife (or kids if they study medicine like mine)
force you to eat that.
Fortunately animals like chicken, cows and pigs also eat the plant stuff, turning it into something
useful like steaks or ham which some of us also eat. |
|
 |
Whatever the food chain looks like in detail, one fact applies to everything
that was once alive. As soon as something organic like you dies in some (hopefully far away) time in the future, or the
tree you felled with your car, or the grass that withered in the sun, there is now some dead body around that contains a
lot of carbon that came exclusively from the carbon dioxide in the air via the food chain.
Now something special happens.
The carbon in the dead organic matter slowly changes over the years. And with carbon I mean the individual carbon atoms, no matter in what kind of molecules they find themselves as time goes by. When you're
dead you rot and turn to compost but this involves only chemical reactions that change
the molecules but not the atoms. The basic insight is that all the oxygen, hydrogen,
phosphorous, nitrogen and so on atoms do not change at all - except for the carbon atoms.
We need to answer two basic
questions now: |
 |
1. How can an atom
change itself? There are two basic ways:
- The nucleus of an atom, the tiny assembly of protons and neutrons in the center of the atom, emits an elementary particle
like an electron (b - decay), an helium nuclei (2 protons plus 2 neutrons; a
- decay), a positron, or whatever. This is simply radioactive decay and what's left
is a different atom.
- The nucleus of an atom gets hit by some energetic particle like a proton or a neutron in such a way that the composition
of the nucleus changes. Sort of the revers of radioactive decay. A different atom is produced once more.
| |
|
| |
You might wonder about the electrons surrounding any atom - what's
their role in this? None. They just rearrange to whatever is needed. The energy involved for this is minuscule compared
to what's going on in the nucleus and thus can be neglected. |
 |
2. How can some carbon atom
be different from any other carbon atom?
- It's called "isotopes", remember? The number of protons in a nuclei decide
what element it is and thus is fixed, but the number of neutrons can be different for the same number of protons.
- The nucleus of a carbon atom, for example, has always
6 protons (add 6 electrons and you have a carbon atom) but the number of neutrons can be 6, 7 or 8. That gives
us three carbon isotopes: 12C, 13C, and 14 C.
| |
|
| |
The last thing to remember now is that some isotopes are stable forever,
some decay radioactively. As it turns out, the carbon isotopes 12C and 13C are stable. 14C,
however, decays with a halftime of 5 730 ± 40 years. In other words, if you start with 1 000 14C atoms,
you will only have 500 left after 5 730 years. 250 after 2 ×5 730 years = 11 460 years, and so on. |
| |
|
| |
How It Works |
 |
All elements where made some time ago (like 10 billion years or so), either in
the big bang or inside a sun. The ratio of the isotopes of a given element was fixed right then, and all the radioactive
ones have long since disappeared (with a few exceptions that are of no interest here). The ratio of 12C to 13C
thus is fixed at 99 : 1, and this ratio is immutable.
There is no 14C left over from the times when all
the carbon atoms were made. |
|
 |
However, the atmosphere of our planet consists of 78.08% nitrogen molecules (N2),
20.95% oxygen molecules (O2), 0.93% argon (Ar), 0.038% carbon dioxide molecules (CO2) plus traces
of other stuff of no importance here. What is of importance here is that all these molecules and atoms in the upper strata
of the atmosphere get hit by highly energetic particles of the cosmic radiation that bombard the earth relentlessly all
the time. The atmospheric layers up there stops most of this radiation. That is generally a good thing for normal people
because we would not be here or last very long if we would be hit by that radiation.
It is also a good thing for archeologists
because some of that radiation hits nitrogen atoms and turns them into the 14C isotope. The precise reaction
is |
| | |
|
|
|
| n | + |
14
7 | N |
Þ |
15
7 | N |
Þ |
| 14
6 |
C | + p |
|
|
| | |
|
|
 |
In words: A nitrogen atom with (per definition) 7 protons and 7 neutrons (adding
up to 14N) gets hit be a neutron (n) that was supplied by cosmic radiation, and turns into the unstable 15N
isotope that decays immediately into 14C by emitting a proton (p).
In yet other words: In the upper atmosphere
14C is generated at a constant rate. It trickles down, forms carbon dioxide, and gets incorporated into plants
and finally into everything alive. It decays inside you but as long as we live, we replenish it and essentially keep up
a constant level of 14C in our organic bodies. As soon as we die, no more 14C is added to the remains
and whatever was there now decreases in concentration by a factor of two every 5 730 years. |
 |
Radiocarbon dating now is easy. Measure the relative concentration of the14C
isotope in living (or freshly dead) organic material, and you have the starting point. It is about 1 part per trillion,
i.e. you have about 600 billion radioactive carbon atoms in one mol of carbon. A mol
is a defined amount of stuff. |
|
 |
If the organic matter you unearthed somewhere (typically coal from some old fire,
bones or wood remains; all containing carbon) happens to be 5 730 years old, you would find only half of that concentration
or only 300 billion radioactive carbon atoms in one mol of carbon.
With a little simple math, the "Before Present" or BP age tBP of a sample comes out to |
| |
|
| |
|
| tBP |
= – 5 730 years |
· |
log2 |
N
N0 |
|
|
| | |
|
|
 |
N is the measured 14C concentration; N
/ N0 thus the relative concentration of how much 14C is left. This follows straight
from our old beer math. |
 |
Is that cool or what? So of course you know everything about the hero of science
who came up with that monumental recipe for dating old organic things: Willard
Frank Libby and his team at the University of Chicago first came up with the method in 1946; Libby got the
Nobel price in 1960. |
|
 |
The basics are clear now. It only remains to look at the small print coming with
the general recipe for 14C dating. We need to answer two big questions:
- How do you measure those extremely small amounts?
- How reliable are the results you get, or in other words: how large are the error margins and what determines their magnitude?
|
| | |
|
| |
How It Is Done |
 |
How is it done? Well - the stuff is radioactive after all! So get a Geiger counter
or whatever else registers radioactive decay, hold it over your sample, and measure how many "clicks" you get
per time unit (= N). Repeat with a sample of modern carbon that contains exactly as much carbon as the sample
you want to date to give you the N0. Use the equation form above and you are done. |
|
 |
OK - that's how Libby did it, and there are problems, of course. From tiny samples
you don't get that much signal, so your N value has an error of roughly N
½. Your N0 value has an error - and how do you determine
the exact weight you need (or just the exact carbon weight of your sample)? Than your halftime value may be a bit off. In
fact, Libby used a value of 5568±30 years that was later corrected to 5730±40 years.
Maybe your sample as
contaminated with a bit of "fresh" carbon? The tree those Greek guys used to barbecue their rabbit was a 500 year
old oak that was felled by a flash of lightning - your are 500 years off the proper date of the fire! An so on.
The
most tricky source of error, however, is that the 14C/12C ratio for "fresh" carbon is not
really constant as was assumed as a matter of course. This may have several reasons:
- Some of the cosmic radiation comes from our sun, and she is not totally reliable but wiggles the intensity a bit every
now and then.
- The magnetic field of the earth influences cosmic rays somewhat (it deflects them to some degree). The magnetic field
of the earth changes on large time scales and so does the 14C/12C ratio.
- The earth also exchanges carbon from the soil or from the oceans with the atmosphere at fluctuating rates, influencing
the 14C/12C ratio.
- And so on. Supernova explosions nearby may increase the cosmic radiation intensity for a while or maybe not. We just don't know.
|
 |
Since we have some more methods to date things, and since more and more details
become clear, we now have a calibration curve: |
| |
| |
| |
|
| | |
|
|
 |
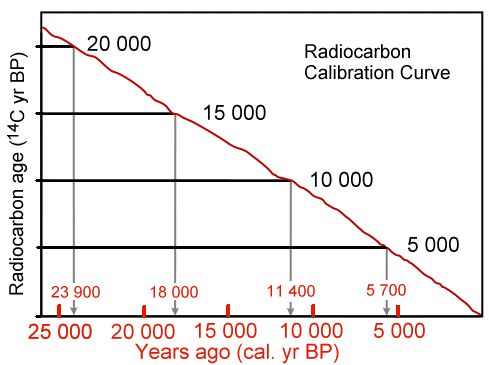
As the examples show, a radiocarbon age of 20 000 (10 000) years translates into
23 900 (11 400) BP years or 21 900 (9 400) BC. So be careful about the BP and the BC! With this curve we get rid of the
fluctuating 14C/12C ratio problem, at least to some extent. We are also rather certain that the halftime
is now as correct as it can be. The only problem that remains is to measure the amount of 14C still there. That
gets more difficult for old thing because most of it has already decayed and thus disappeared, and for very small specimen
that do not contain much to start with. The decay rates then are so low that they do not register anymore in your Geiger
counter or more sophisticated equipment. |
 |
That's when "accelerator mass
spectrometry
" (AMS)
kicks in. This is rather tricky (and very expensive) but allows a far better analysis of the 14C/12C
ratio for far smaller samples than the direct method. |
| |
 |
How does it work? You atomize your specimen, ionize the carbon (and whatever
else will get ionized), accelerate those ions by high voltage, run them through a thin film to strip off electrons in order
to destroy all charged molecules (like 13C1H) that might be in there and would be confused with 14C,
accelerate the pure ions now once more with a really high voltage (several million Volts), and separate different atoms
and their various isotopes by magnetic fields into individual ions beams. Measure how much 14C and 12C
flies along and you have the ratio.
Here is an impression of what is involved (from the Leibniz Laboratory for Radiometric
Dating and Stable Isotope Research of my University (Christian-Albrechts-University of Kiel, Germany). |
| |
|
| |
|
 |
| Hardware for accelerator mass spectrometry |
|
| | |
|
|
 |
Doesn't look cheap, isn't cheap, and is not all that easy to operate. You need
to know exactly what your are doing, in particular with respect to specimen preparation. The data you get are only as good
as your specimen. Breath at it once in the wrong way, and its contaminated with fresh carbon, yielding faulty results. |
 |
Not sparing time and money, how good can it be? Well, after about ten half-lives,
approximately 60,000 years, not much 14C is left (1/ 210) » 1/1
000). That gives sort of the lower limit for a 1 mg sample. Very young stuff is problematic too, but why should you want to date that?
|
| |
 |
Pure iron, copper, gold and so on, not containing any carbon, cannot be dated
this way at all, of course. But what about steel? It contains carbon and that we can dated. Yes - but where did that carbon
come from? If it came exclusively from the charcoal used in the smelting process, you get the age of the tree the charcoal
was made from, and that should be close enough. However, if some of the carbon came from the limestone or calcium carbonate
(CaCO3) that was added for some reason, or if you used coal (from trees that died many million years ago) your
results are useless. |
| |
| |
© H. Föll (Iron, Steel and Swords script)