Defekte in Kristallen: 1.3.3 Zoologie am Beispiel Silizium

1.3.3 Eigenschaften atomarer Fehlstellen

"Zoologie" am Beispiel des fcc Kristalls Silizium

	Dieses Unterkapitel soll verdeutlichen, daß das zunächst simple Konzept von Leerstelle und Zwischengitteratom in realen Kristallen rasch recht komplex werden kann. Dies gilt schon für den einfachsten Realkristall, dem fcc-Gitter mit einem Atom in der Bassis, und noch mehr für Si (fcc mit 2 Atomen der gleichen Sorte in der Basis). In wirklich komplizierten Kristallen, in denen es mindestens soviel Leerstellensorten wie verschiedene Atome (und erheblich mehr ZGA-Sorten gibt), wird es schnell unübersichtlich.
		In den 70er und 80er Jahren wurde ein weltweiter erbitterter Streit um die exakte Struktur des Zwischengitteratoms in fcc-Metallen geführt, dessen Champions zwei große deutsche Grundlagenforschungsinstitute waren; er ist bis heute nicht wirklich entschieden. Seit ca. 1975 läuft ein ebenfalls noch andauernder Streit über die Art der intrinsischen atomaren Fehlstellen in Si. Wir lernen daraus, daß atomare Fehlstellen alles andere als einfach sind!
	In diesem Kapitel werden wie in einer Ouvertüre viele Leitmotive (im Sinne von Phänomenen und Schlagworten) angespielt, die später ausführlicher behandelt werden. Hier soll zunächst nur vermittelt werden, daß zwar viele Technologien auf den Eigenschaften atomaren Fehlstellen beruhen, daß aber viele Fragen noch offen sind.
	Als Startpunkt für eine Reise in die Komplexität der atomaren Fehlstellen betrachten wir eine simple Leerstelle oder ein Zwischengitteratom im kubisch flächenzentrierten (fcc) Silizium im thermischen Gleichgewicht (die Betrachtungen gelten im Prinzip aber auch für viele andere Kristalle). Zu beachten sind:
	Atomare Struktur
		Dies scheint bei Leerstellen einfach; aber wie "ausgedehnt" ist der Defekt? Eine Leerstelle könnte man (gedanklich) auch erzeugen, indem man z.B. 11 Atome herausnimmt, und 10 wieder einfüllt (füllt man 12 wieder ein, hätte man ein "ausgedehntes" ZGA). Gibt es so etwas? Wie kann man solche ausgedehnten Defekte von "normalen" unterscheiden?
		Bei Zwischengitteratomen gibt es selbst in einfachen Elementkristallen viele Möglichkeiten der Anordnung: "Hanteln", d.h. zwei Atome symmetrisch auf dem Platz von einem; das ZGA in der Oktaederlücke oder in der Tetraederlücke
		Es gibt aber noch mehr Möglichkeiten; z.B. das "Crowdion", das als metastabiles ZGA in fcc Metallen bei tiefer Temperatur vorkommen soll und um das der o.e. Streit ging, oder das "extended interstitial" in Silizium, ein postuliertes ausgedehntes ZGA bei hoher Temperatur im Si, das bisher auch nie ganz von der Fachwelt akzeptiert wurde, aber in den letzten Jahren an Boden gewinnt.

	Mögliche Änderungen der atomarer Struktur von ZGA mit der Temperatur. Die größere "Unordnung" bei höheren Temperaturen erlaubt evtl. einen (reversiblen) Übergang vom einfachen Zwischengitteratom zu einer Anordnung als extended interstitial oder "ausgeschmiertes ZGA" in Si (obere Skizze). Das postulierte Crowdion (unten) kann, falls bei tiefer Temperatur durch Bestrahlung erzeugt, zunächst in der metastabilen, in <110> Richtung elongierter Form vorliegen. Beim Erwärmen geht es dann irreversibel in die normale Form über. .
	Ladung (in Halbleitern und Ionenkristallen)
		In Ionenkristallen müssen atomare Fehlstellen notwendigerweise geladen sein, da insgesamt Ladunsgneutralität vorliegen muß.
		In Halbleitern kann der Defekt ein Zustande im band-gap haben; wie die Dontoren und Akzeptoren. Wechselt die Fermi-Energie von unterhalb zu oberhalb des Defektniveaus, wird der Defekt eine negative Ladung erhalten, also z.B von neutral oder einfach negativ zu einfach negativ oder zweifach negativ umgeladen. Der vorliegende Zustand hängt damit von der Fermienergie ab. .
	Kopplung Ladung - Struktur (führt zu athermischem Diffusionsmechanismus nach Bourgoin)
		Ein beliebiges Beispiel dazu: Das neutrale ZGA sitzt in der Oktaederlücke, das positiv geladene in der Tetraederlücke. Bei jedem Wechsel des Ladungszustands erfolgt ein atomarer Sprung unabhängig von der Temperatur.

Intrinsische Defekte im thermischen Gleichgewicht

Obige Liste verdeutlichte, was alles vorliegen könnte. Dabei wurde nicht nur phantasiert, sondern auf bisherige Erkenntnisse und Fragestellungen abgehoben. Was liegt nun aber unter idealen Bedingungen (=perfekter Kristall) im thermischen Gleichgewicht wirklich vor? Während man für die gebräuchlichsten fcc-Metalle diese Frage einigermaßen beantworten kann, ist aber ausgerechnet im Silizium die Natur der intrinsischen Defekte nicht vollständig geklärt. Von der einfachen Frage nach den Konzentrationen von Leerstellen und Zwischengitteratomen als Funktion der Temperatur, bis hin zu vielen weiteren Fragen erstreckt sich der Bereich der aktuellen Forschung. Zur Bedeutung der intrinsischen atomaren Fehlstellen in Si genügt es zu erwähnen, daß sie die Diffusion der Dotierungselemente Bor, Phosphor und Arsen vermitteln, und damit die Grundlage der gesamten Halbleitertechnologie bilden

Atomare Fehlstellen im Nichtgleichgewicht

	Während im thermischen Gleichgewicht letztlich meistens nur eine Varianten der möglichen atomaren Fehlstellen vorliegen wird (weil diejenige mit der kleinsten Bildungsenthalpie dominiert), kann die Lage im Nicht-Gleichgewicht komplex werden. Das globale Gleichgewicht mit der absolut tiefsten freien Enthalpie läßt sich nicht immer erreichen, als "zweitbeste" Lösung wird der Kristall ein lokales Gleichgewicht anstreben. 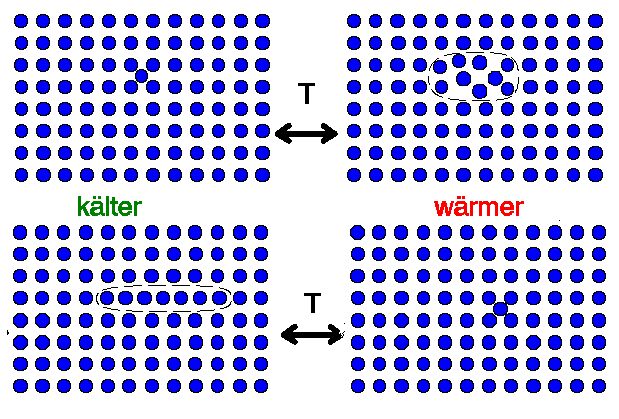Ein Nicht-Gleichgewichtszustand entsteht immer, wenn man vom Gleichgewicht ausgehend die Temperatur ändert. Zur Einstellung eines neuen Gleichgewichtes müssen kinetische Prozesse ablaufen, bei denen immer atomare Fehlstellen erzeugt oder vernichtet werden müssen. 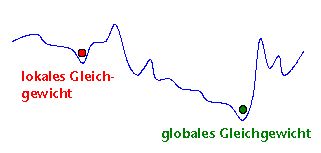Ein übliches Bild zur Verdeutlichung ist ein Potentialgebirge mit mehreren Minima, von denen nur eines ein absolutes Minimum entsprechend dem globalen Gleichgewicht sein kann. Ein Zustand in einem Seitenminimum (=lokales Gleichgewicht) kann meist nur über eine Energiebarriere in das globale Gleichgewicht übergehen. Reicht die Temperatur zur Überwindung diese Barriere nicht aus, wird globales Gleichgewicht nur langsam oder nie erreicht.

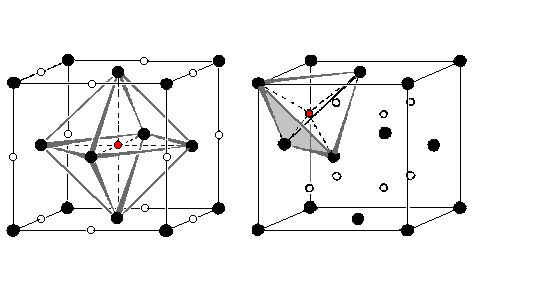
		Eine Reaktion, die globales Gleichgewicht herstellen könnte, ist z.B. die gegenseitige Vernichtung von Leerstellen und Zwischengitteratomen, falls es zuviele davon geben sollte (z.B. nach Absenken der Temperatur). Die zu überwindenden Potentialbarrieren sind zunächst die "Wanderungsenthalpien", es können aber auch neue Phänomene auftreten, z.B. "Entropiebarrieren" bei der Vernichtung von ausgedehnten Defekten .
	Wirklich kompliziert wird es, wenn schon die primäre Erzeugung von atomaren Fehlstellen im Nicht-Gleichgewicht erfolgt ("mit Gewalt"). Möglichkeiten dazu gibt es viele:
		Kristallwachstum: Der Einbau von (intrinsischen) atomaren Fehlstelle direkt beim Kristallisieren könnte im Nicht-Gleichgewicht erfolgen. Dies wurde für bestimmte Defekte in Si Kristallen heiß diskutiert.Ein allgemeinverständlicher Artikel dazu findet sich im Link (Swirls in Si: Geichgewicht oder Nichtgleichgewicht? (1,6 MByte))
		Abschrecken:, d.h. sehr schnelles Abkühlen. Damit atomare Fehlstellen nach wenigen Diffusionssprüngen verschwinden können, müßten Senken in hoher Dichte vorliegen - kaum machbar.
		Plastische Verformung, insbesondere Klettern von Versetzungen (Ist in den 2-atomigen optoelektronischen Kristallen (z.B. GaAs) der Grund für die Degradation von Laserdioden)
		Bestrahlung durch Elektronen (wir praktisch nur für wissenschaftliche Zwecke gemacht); Ionen (Ionenimplantation; insbesondere für Halbleiter-Technologie), Neutronen (z.B. für die "Neutronendotierung" von Silizium), a-Teilchen,.. (z.B. bei Kernspaltungs- aber auch Kernfusionsreaktoren), g-Strahlen,..
		Oxidation von Silizium (injiziert Zwischengitteratome)
		Nitridation von Silizium (injiziert Leerstellen)
		Reaktive Grenzflächen ganz allgemein (z.B. Silizierung) können atomare Fehlstellen erzeugen
		Ausscheidungsvorgänge (SiO₂-Ausscheidung erzeugt, SiC-Ausscheidung verbraucht Zwischengitteratome)
		Diffusion (z.B. Phosphor-Diffusion in Silizium) .
	Beispiel für die Relevanz lokaler Gleichgewichtseinstellung: Bei der Zucht von immer größer werdenden Silizium-Kristallen (eine 8 Milliarden $ Industrie) stößt man immer wieder auf massive, durch atomare Fehlstellen verursachte Probleme, da die im thermischen Gleichgewicht vorhandenen AFs beim Abkühlen nicht verschwinden können und sich zu /störenden) Agglomeraten zusammen tun. (12 kByte)
		Swirl-Defekte (1,6 MByte) in der Unterteilung nach A- und B- Defekten waren das Thema Ende der 70er Jahre (führten auf die Existenz des Zwischengitteratoms in Silizium)
		D-Defekte (der Name verrät schon, daß man nicht genau weiß was das ist) sind zur Zeit die "heißen" Defekte im Si-Kristall .
	Zum Schluß noch einige Illustration zu diesen Punkten
		"Atomare Fehlstellen" mit dem Raster-Tunnelmikroskop sichtbar gemacht
		Ätzmuster von A- und B-Defekten (145 kByte) ("Swirls") in 4 Zoll float-zone Silizium (4´´ FZ-Si). Hier sieht man die Spuren der durch Agglomeration vieler AFs entstandenen großen Defekte.
		Sauerstoffring und D-Defekte, sichtbar gemacht mit dem ELYMAT