|
What kind of properties need a material have to have, so it linearly
polarizes light? |
|
 |
For starters: if you run the light through the material,
it needs to be transparent. But who says that you can only polarize light by running it through
a material? How about bouncing it off some material or, in other words, reflecting it
at some mirror-like surface? |
|
 |
This should trigger a flash-back. As you already know, it is perfectly possible to polarize
light by utilizing reflection; just look once more at the Fresnel equations. |
 |
All things considered, there are several ways to polarizes light, each one with
its own requirements, advantages, and disadvantages. Here we'll just take a first glimpse at some major polarizing methods. |
 |
1. Special geometries. |
|
 |
As we have learned under the heading "Fresnel
equations", a non-polarized light beam impinging on any material
under some special angle ("Brewster angle")
will produce a fully polarized reflected beam. Of course, some materials are more suitable
than others (the index of refraction should have a decent value, not too close to n=1 but not too large either)
but no special properties of the materials are required. |
|
 |
Using the "Brewster angle" approach is indeed a major way to produce polarized light.
It is more or less limited to "advanced" application, however, because there are some problems. Time for a quick
exercise: |
| |
|
|
 |
For everyday applications like your "Polaroid" sun glasses or the cheap glasses
used for watching 3D movies in the cinema, you need something less special and far, far cheaper. You need: |
 |
2. Polarization filters or foils |
|
 |
We have a typically thin and bendable transparent foil (or a thin unbendable
glass-like sheet). Unpolarized light goes in from one side, linearly polarized light
comes out on the other side. There are two basic ways or principles for that:
- The material contains "nanorod" conductors arranged in a grid with dimensions in the wavelength region.
- The material is "birefringent" or in neutral terms, it is optically
anisotropic, meaning that e and therefore also n are tensors.
|
|
 |
The bad news are: The second principle is the more important
one!
The good news are: We are not going to
look at that in great detail, since there is not enough time. Tensor optics also may cause the bulk intake of large quantities
of alcohol to soothe your brain, and you are too young for this. |
 |
The first principle is easy to understand: |
|
 |
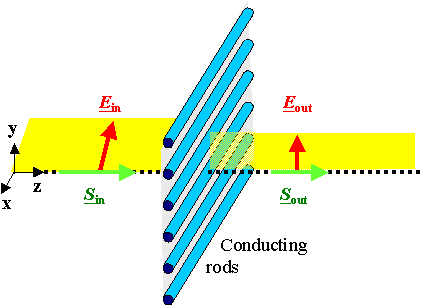
Just imagine for a moment that you need to polarize radio waves
with a wave length in the cm region and not light. All you need to do is to use a bunch of aligned conducting rods as shown below: |
| |
|
 |
Surprise! The polarization direction is not parallel to the rods as one would naively imagine but perpendicular to it. |
|
 |
It's clear what happens, though. The field components parallel
to the conducting rods will simply be short circuited, causing currents j=sE
in the rod, and thus heating. The components perpendicular to the rods cannot cause
much current and pass mostly through. The figure above, by the way, is identical to a figure we had
before except that the symbolic polarizer in this picture has now materialized into a defined device or product. |
|
 |
If you wonder about possible diffraction effects at the
grid: There aren't any if the distance between the rods is smaller than a wavelength. Just do an Ewald
sphere construction to see this. |
 |
The priciple, of course, also works for the electromagnetic waves we call light. All that remains
to do, is to produce aligned conductive rods on a 100 nm or so scale; nanorods in other
words. Any ideas? |
|
 |
Well, a guy named Edwin Herbert Land
(1909 - 1991) had an idea - in 1932. Take a polymer foil that can easily be stretched to a large extent (look at this link to get an idea), get some proper stuff inside (microscopic
herapathite crystals in Lang's case; funny things in their own right
involving dog piss), and then stretch the whole foil, aligning the little
crystals. Use the link to get the full story. |
|  |
I don't know what Lang thought when he did this. Some people (and text books) believe that
he did align conducting rods, indeed. Chances are that he did not, however. The herapathite
crystals in Lang's case are actually very complex crystals; their structure was found out only a few years ago. Herapathite
(also known as Chininbisulfatpolyiodid) forms intrinsically polarizing crystals,
and all the stretching of the foil just insured that their polarization axes were aligned. |
 |
So back to square 1: Any ideas of how to align conducting
nanorods on a 100 nm or so scale? |
|
 |
Of course you have an idea: Use the basic micro (or by
now nano) technologies of semiconductor
technology and produce something as shown in the picture below |
|
|
 |
| Si nanorods (actually rather microrods but one could make them smaller if required) |
|
|
 |
The rods shown consist of Si
and they would certainly polarizes (IR) light besides doing a few more things (due to their 3-dim.arrangement).
It's however not a practical way for cheap mass-production stuff. Moreover, while light coming out on the "other"
side would certainly be linearly polarized, one can just feel that it would not be a lot of light that makes it through
the structure. More about this structure (which was not made for optics but for something utterly different) in the link. |
|
 |
If we look a bit beyond "normal" optics into the far UV and IR, polarizing
a beam is not all that easy and structures as shown above might be the "future" in this case. Here is the link for some more information about this. |
|  |
Time for the famous last word: I could not find out in April 2011 if there are actually (cheap)
polarizing foils out there that actually work on the "conducting rod" principle. So let's go for a third
way. |
 |
3. Polarizing materials |
|
 |
A good polarizing material, e.g. some crystal and not
a "foil", transmits an incoming beam without too much absorption and emits one or even
two beams that are more or less polarized. |
|
 |
We can already make one statement about the properties such a material must have: All directions
must not be equal since the polarization direction is per definition special. Isotropic
materials like most amorphous stuff and all cubic crystals, thus cannot
be polarizing materials. |
|
 |
A stretched polymer foil is no longer isotropic since the polymer chains now are somewhat
aligned in the stretching direction. However, it will not necessarily polarize light. Try it!.
Stretch some suitable candy wrap and see if it now polarizes light. Changes are it will not. So just being structurally
anisotropic is not a good enough condition for being a polarizer. |
 |
That means we must now deal with not-so-simple Bravais lattices, crystals, or other structures.
It also means that properties like the dielectric constant er and thus the
index of refraction n, the conductivity sr, possible magnetic
properties, the modulus of elasticity (Young's modulus) and so on are no longer simple scalar
number but tensors
of second, third or even fourth rank! We are now discussing crystalline "optical tensor materials". |
|
 |
Talk about opening a can of worms! Nevertheless, understanding and exploiting the tensor properties
of materials (mostly crystals) is where the action is right now (2011), and where it will be for the foreseeable future.
At this point I will only enumerate some of the important effects of tensor materials on polarization. |
| | |
|
Optical Anisotropy and Tensor Materials |
| |
|
 |
The basic ideas are easy to state. First, if there is an optical anisotropy, it
can take two basic forms (and then mixtures of the two, of course): |
 |
1. The index of refraction depends on the crystal direction. The optical
effects resulting from this are called "birefringence" or double
refraction (Latin: bi=two, twice, refringere=to break up, to refract). |
 |
2. The absorption depends on the polarization (and the crystal direction).
In some directions far less light of some polarization will come out after travelling through a crystal of given thickness
than light polarized in the other direction. This effect is called dichroism (Greek for two-colored).
|
|
 |
It is an unfortunate word because historically it was used first for a different
effect: White light is split into into distinct beams of different wavelengths because of the crystal anisotropy and this
is completely different from regular dispersion! Since the absorption effect may strongly depend on the wavelength, too,
everything can be mixed up wonderfully. The word "pleochroism" ("more-colored")
is occasionally used as a more general term, containing all of the above. |
 |
You know, of course (?) that the two effects must be related because they must both be contained
in the complex index of refraction, which simply (haha) happens to be a tensor
now. All tensor components are functions of the wavelength because we still have dispersion
and, since we also have the Fresnel equations,
they must be functions of the polarization, too |
 |
All we need to do now is to run through the derivation of the Fresnel equations once more.
Just consider now a complex index of refraction that is also a tensor of of second rank with a symmetry that is somehow
related to the crystal symmetry instead of a scale for boundary conditions and propagation. That would be a program that
could entertain (some of) us for many weeks - so we are not going to do it here. |
|  |
It is important to realize, however, that with our modern computers this is actually an easy task. As soon
as a basic program has be written, and the functions describing the tensor components of the complex index are inputted,
the rest is child's play. That's why for you, the young Materials Science and Engineer, the complex index is so important.
For old guys like me it was not important, since we simply couldn't do the necessary math with a slide ruler as the only
math tool. We had to resort to approximations and special case studies, and that's where all these fance names and distinctions
comes from. |
 |
We are going to give the whole topic just a very superficial look, focussing on the practical
side. As a first simplification we simply ignore di- or pleochroism for the time being and only give birefringence
a slightly closer look. We also ignore absorption and thus the imaginary part of the complex index of refraction. |
|
 |
Recalling the little bit what we
know about tensors, we are certain that there is always a coordinate system or "axes", where only the diagonal
elements of the refractive index tensor are different from zero. These axes we call the principal
axes of the crystal under consideration. |
|
 |
We then can always define three
principal refractive indices
n1, n2, n3 as the tensor components in the principal
axes system. Note that those n's will depend on the polarization and the wavelength. Of course, the principle
axes will be related to the symmetry of the crystal in some way. |
|
 |
The rest is math. Not too difficult if you are used to tenor algebra but a bit mind boggling
for normal people like us. For example, the dielectric displacement D or the Poynting vector S
may no longer be parallel to the electrical field E or the wave vector k, respectively.
Now what would that mean? |
 |
Be
that as it may, the fact of importance here is that in general, an unpolarized light
beam entering an anisotropic crystals splits into two orthogonally polarized light beams
inside the birefringent material (typically a single crystal, a collection of small aligned single crystals, or an amorphous
foil "somehow" made anisotropic and birefringent). Two different light beams
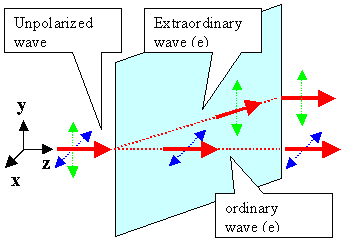
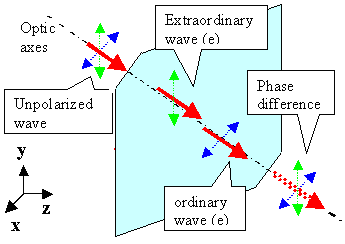
thus will run through the crystal and eventually exit on the other side as shown below. |
| |
 |
 |
Incoming beam not along optic axis
(see below), but at right angle to some surface.
Þ No change of direction under "ordinary" circumstances and for the ordinary beam. Pronounced change of direction for extraordinary
beam. |
Incoming beam along optic axis (see beleow) and at right
angle to surface.
Þ No change of direction under "ordinary" circumstances and
for both beams in birefringent material. Both beams run parallel but with different
velocities. |
|
 |
The two figures above illustrate the basic effects that will occur. It is best to discuss birefringences
for the two special cases shown |
 |
1. case: The incoming (unpolarized) beam is not
parallel to a principal axis of the crystal but its angle of incidence is 90o, i.e. it is exactly perpendicular
to the surface of the crystal. This is a special condition, but not so very special because it is easy to do in an experiment,
All you need are some flat surfaces. |
|
 |
For an isotropic material with a scalar
index of refraction n we know that there will be no refraction
or bending of the beam. A little bit will be reflected (see the Fresnel equation),
and the polarization does not matter. The transmitted beam will travel through
the material at a velocity c=co/n. |
|
 |
Exactly the same thing happens for the ordinary wave or
o-wave in our tensor material here. However, the o-wave now is fully polarized as shown
|
|
 |
But in major contrast to isotropic materials with a scalar n, an extraordinary
thing happens in our birefringent material with a tensor
n. An extraordinary wave or e-wave is also generated at the
interface. This e-wave travels under some angle with a velocity that is different
from that of the o-wave. The e-wave is also fully polarized, but with
a direction orthogonal to that of the o-wave. |
 |
2. case:
The incoming (unpolarized) beam is parallel to an optical
axis of the crystal, and its angle of incidence is still 90o, i.e. it is exactly perpendicular
to the surface of the crystal. This is a rather special condition now because it means that our crystal must have a planar
surface perpendicular to an special crystal direciion. |
|
 |
The so-called optic axis of the birefringent crystal is coupled
to our principal axes from above. We have something new now (or just an extreme
case of the general situation). |
|
 |
The o-wave and the e-wave travel in the
same direction=optic axis but with different velocities.
Both waves are still fully polarized in orthogonal directions. |
|
 |
The two waves emerging form the crystal then have different
phases. The exact phase difference depends on the distance covered inside the material, i.e. on the thickness
of the material. |
 |
That's just a description of what you will observe, of course. Calculating the relative intensities
of the two beams, the intensities of reflected beams (??? (there is only one)), the two angles
of refraction, the polarization directions, and the propagation velocities from the index of refraction tensor is possible,
of course—but well beyond our scope here. |
|
 |
One question remains: How many optic axes are there? The answer is: Two
for "fully" anisotropic material and one for somewhat more symmetric materials.
That tells you that the optic axis and the principal axis are not the same thing because we always have
three pricipal axes. It's all in the table below. |
|
|
| Dielectric tensor in principal axes |
| Anisotropic Materials |
Isotropic Materials |
| er |
= |
æ
ç
è
|
e1 0 0
0 e2 0
0 0 e3 |
ö
÷
ø |
|
| er |
= |
æ
ç
è
|
e1 0 0
0 e1 0
0 0 e3 |
ö
÷
ø |
|
| er |
= |
æ
ç
è
|
e1 0 0
0 e1 0
0 0 e1 |
ö
÷
ø |
| General case
Two optical axes |
Practical case
One optical axis |
Simple case
All directions / axes are equal |
| Mica |
e3 > e1
Positive
uniaxial |
e3 < e1
Negative uniaxial
|
Glass
Diamond
Cubic crystal
(NaCl, CaF2, Si, GaAs, ..) |
Ice
quartz
TiO2 (rutile) |
Calcite (CaCO3)
Tourmaline
LiNbO3 |
|
 |
I can't end this chapter without a quick reference to the ubiquitous direct effect of birefringent
crystals discovered long ago. There is deceptively simple effect already known
to Huygens and Co: Take an "Iceland spar" crystal
(CaCO3 or calcite; easy to get), put it on some paper with
writing on it and you see everything twice (see below). |
|  |
Here are some pictures taken in my office: |
|
|
 | | Birefringence with a calcite crystal |
|
© H. Föll (Advanced Materials B, part 1 - script)