5.1.2 Basic Geometric Optics

The Very Basics of Geometric Optics

	The essence of basic high-school geometric optics is shown in the following pictures:
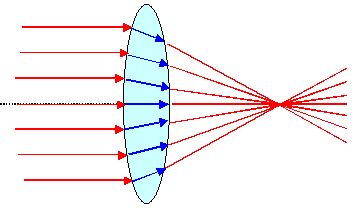
		Reflection and Refraction Focussing by an ideal convex lens
		Optically transparent materials ("glass") have an index of refraction n > 1, and light hitting a transparent material is reflected and refracted. Convex (or collecting or converging) lenses and concave (or dispersing or diverging) lenses allow to manipulate the light path, e.g. by focusing a parallel beam of light as shown.
		Let's clarify the terms at this point:
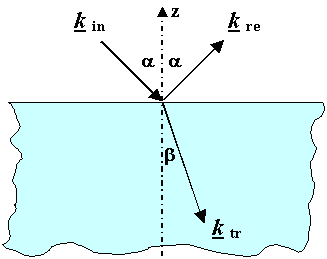
		Reflection is, well, reflection; always with "angle in" = "angle out". Refraction is the sudden "bending" or "flexing" of light beams at the interface between two different materials. The term belongs to geometric optics. A light beam going through a lens is refracted. Diffraction is the continous "bending" of light beams around corners and all the other effects bringing about directional changes and interference effects. A light beam going through an optical grid is diffracted. The term belongs to wave optics.
	The decisive material quantity in geometric optics (and beyond) is the index of refraction together with Snellius law.
		What we know about Snellius law and some other basic optics parameters like the speed of propagation c inside materials, frequency n and wavelength l in materials or in vacuum, is
		sin a sin b  =  n Snellius law       n  =  c0 c   =  er1/2   From Maxwell equations       c  =  n · l Always valid       lmat  =   1 n  · lvac    From the equations above
	Knowing only the index of refraction n makes it already possible to construct light paths or light rays running through optical devices like lenses or prisms.
		Going a bit beyond that, we would also like to know the the optical dispersion, i.e. n = n(n) so we can construct light paths for the various frequencies (= colors) of visible light. Obviously, all we need to know for this is the frequency dependence of the dielectric constant e(n), something we have treated extensively before.
	A nice thing in geometric optics is that the direction of the light paths is always reversible. Change the arrow directions in the picture above (or in all other pictures like that) and they are still correct.
		A not-so-nice thing might be that the definition of n = er1/2 becomes troublesome if e < 0, which, as we know, is perfectly possible. Could there be an imaginary or even negative index of refraction? The answer is yes - as you will see later.
	If we go one step beyond simple geometric optics with ideal lenses, we realize that some modifications need to be made:
		Real lenses have all kinds of problems called lens errors or lens aberrations. Some light is always reflected at interfaces between media with different indices of refraction. The intensity of the light is always attenuated or damped whenever it passes through a material. Focal "points" have finite dimensions in in the order of the wave length of the light. All of the above may depend to some extent on the polarization of the light.
		In going from point 1 to point 5 we move, of course, from geometric optics to wave optics.
	Let's look very briefly on the first point. The major lens aberrations are:
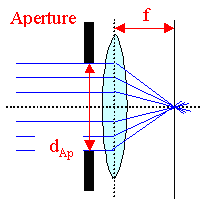
		Spherical aberration. Following Snellius' law, and tracing the light rays for spherical lenses, it becomes clear that light rays running not close to the center of the lens are focussed to a point different from those close to the lens. The effect is small if some aperture keeps the light rays close to the optic axis. The lens then has a small numerical aperture NA. The NA for a single lens is roughly the quotient of (possibly aperture defined) diameter / focal length; i.e. a crude measure of the size of the lens; see the picture below. Of course, lenses with small NA will not suffer much from spherical aberration but will also not transmit much light and thus produce "dark" pictures. The solution might be aspherical lenses but usually combinations of spherical lenses are used.
		Chromatic aberration. Different wavelengths or "colors" are not focussed on the same focal point because we always have some dispersion and the index of refraction is a function of the wave length; n = n(l). The "solution" is the achromatic lens, always a combination of two lenses made from different glasses with n = n(l) or dispersion curves that compensate the effects of chromatic aberration to a sufficient extent.
		Astigmatism occurs if the radius of curvature defining the surface of a lens is not exactly the same everywhere (probably true for the lens in your eye). Instead of a focal point you get a smeared out longish spot. A similar effect applies even to perfectly hemispherical lenses if the light rays coming in are inclined relative to the optical axis.
		And so on. It is almost a miracle that we can see so well using a rather imperfect lens, and that sophisticated optical apparatus like your binocular or camera objective is not only extremely good but also dirt cheap.
	It is of considerable interest for Materials Science that the electromagnetic lenses used in electron microscopes have pretty much the same "aberration" problems as optical lenses, causing all kinds of trouble. Unlike optical lenses, however, there are usually no "easy" fixes except using small apertures, i.e. small NA values.

	A few Examples
	Note: If what follows doesn't bore you to tears, you have a problem!
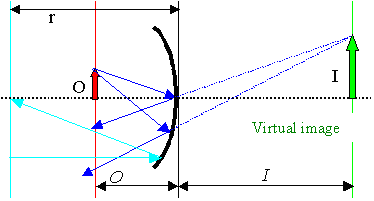
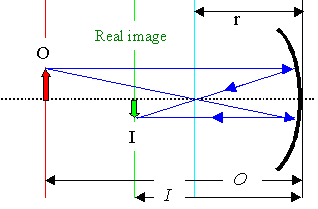
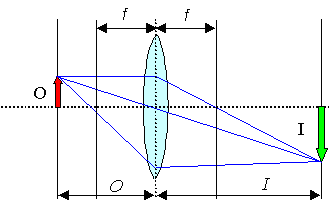
	Imaging through a convex lens. The lens has a focal length f; always a positive number. The Object O is at a distance of O cm, the image I will occur at a distance I cm.
		NA » dAp f Focal length f f = r 2 r = radius of curvature Imaging equation 1 O  +  1 P  =  1 f
		That's what the geometric construction looks like. We call the picture "real" if it is on the other side of the lens as seen from the object.
		The focal length is the decisive number for the lens, next would be its numerical aperture (roughly given by its lateral size). For convex lenses the focal length is a positive number, for concave lenses it is a negative number!
		Instead of the focal length f one often gives values of dioptre D (or diopter), which is simply D = 1/f. My reading glasses with 3 diopters thus have a focal length of 33 cm.
	From a materials point of view the dispersion properties of the (transparent) dielectric, i.e. n(w) = [e(w)]½ in the optical wavelength region is of supreme importance.
		As we know, at optical frequencies dispersion is always determined by resonance phenomena linked to atomic polarization. We also know, that e, n ® 1 for high frequencies, i.e. for ultraviolet (UV) and beyond. In fact, we don't have a lot of good optical materials with high index of refraction in the visible region. Here are a few numbers.

		Typically diamond is described as the "material" with the highest index of refraction. The semiconductors to the right of it actually beat diamond fair and square - but of course only at frequencies where hn < Eg obtains (Eg is the band gap). At higher frequencies semiconductors are perfectly opaque. Silicon thus is only a good optical material in the infrared (IR) region of the spectrum.
		So what is crown glass as opposed to flint glass? Or any of the umpteenth other varieties of glass? Look it up. As a guide: crown glass is your basic run-of-the-mill "lime" glass (i.e. SiO2 with added Na, K and so on ); flint glass (also known as lead glass) is what "crystal" (English for fancy goblets, tumblers, etc. for wine etc.) is made from; i.e. SiO2 with added lead oxide PbO.

	Now let's image with a concave mirror of spherical shape. We can produce real or virtual images as shown.
		Focal length f f = r r = radius of curvature Imaging equation 1 O  +  1 P  =  1 r
		That's what geometric constructions look like. If the image is on the other side of the mirror as seen from the object, we call it "virtual" image.
		Note that spherical mirrors have severe problems with spherical aberration. That's why you tend to use a parabolic mirror where all light rays coming in parallel to the optical axis are deflected to the same focal point. However, remember the first law of economics? There is no such thing as a free lunch! If the light comes in somewhat inclined to the optical axis of a parabolic mirror, its imaging properties are actually worse than that of a spherical mirror. That's why you always have a long tube on front of the mirror.

© H. Föll (Advanced Materials B, part 1 - script)