|
What is light? You know the answer, of
course. To refresh your memory, here is the definition: |
| |
Light is the common name for electromagnetic waves
with wavelengths just below a micrometer (400 nm - 800 nm).
Light is the common name for photons
with energies just above 1 eV (1,8 eV - 3,2 eV). |
|
|
 |
So we still have the good old dichotomy between the wave picture, championed by Huygens and
the particle picture first championed by Newton.
As you know, Newton lost the fight but was redeemed to some
extent by Einstein in 1905. More to that in the link. |
 |
It is of course quantum theory that reconciles
the otherwise incompatible viewpoints. Either you have some ideas how this works or you don't. In the latter case you need
to do some work on your own. I cannot go into this kind of "details" here. |
|  |
In case of doubt think about what you learned about "electron
waves". For example the y = y0 ·
exp(ikr) wavefunction for a free electron that turned a particle into a wave, and the |y|2 that turns a wave back into a particle. It's just as easy for photons. |
|
 |
If you don't get it - tough luck! We're not doing quantum mechanics here. Just accept and follow the simple
rule: |
| |
For the propagation of light:
use the wave model
For the generation and
disappearance (= absorption) of light:
use the photon model |
|
 |
Now we need to consider a few very basic numbers and relations. |
|  |
The key properties and parameters that should come to mind when considering light propagating in vacuum
or in some transparent material with dieelectric constant er, magnetic permeability
mr (always » 1 for optical frequencies)
and index of refraction n are: |
| |
| Relations concerning light |
| |
Propagation in vacuum |
Propagation in material with index of refraction
n | | Wavelength |
l0 |
l0/n |
| Frequency |
n |
n |
| Energy |
hn = 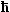 w w |
hn = 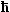 w w |
| Propagation speed |
| c0 | = |
natural
constant |
= n · l |
| | |
|
| | |
= |
(e0 · m0)–½ |
|
| c(n) = |
c0
n |
= |
1
(e0er · m0mr)½ |
| |
| |
|
| |
n | = |
(er · mr)½
» er½ |
| | Wave vector |
|
| |k| | = |
2p/l | |
| | | = |
2pn/l0 |
= | w/c |
| | Momentum |
p = 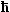 k = k = 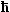 w/c0 w/c0 |
p = 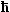 k = k = 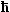 w/c w/c |
| Snellius law |
n = sina/sinb with a, b the angle of incidence or propagation, resp. |
|
 |
We can actually derive all the materials stuff and Snellius law as given in the last entry
very easily by considering energy and momentum conservation. We will do that in a litle exercise. |
| |
|
|
 |
The following table gives a few basic numbers for these quantities that
you must know . |
| | |
| Numbers concerning light |
| |
Rough order
of ten value |
Better value |
| Wavelength |
» 1 µm |
500 nm (390 to 750 nm) |
| Frequency |
» 1015 Hz |
5 · 1015 Hz |
| Energy |
» 1 eV |
2.5 eV |
| c0 (vacuum) | |
300 000 km/s = 3 · 108 m/s |
| Momentum
ratio |
p(2,5 eV electron)
p(2,5 eV photon) |
» | 103 |
|
|
|
 |
The momentum entry serves to remind
you that photons have very little momentum relative to electrons (and phonons) of the same energy. |
 |
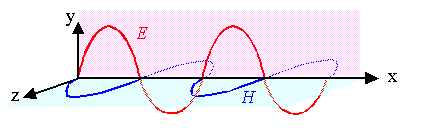
At a slightly higher level of sophistication we remember that light is an electromagnetic wave
consisting of an interwoven electric and magnetic field; E and H. |
|
 |
In complex notation (with the understanding that we only use the real part; in
contrast to quantum theory) a standard plane wave with amplitude E
or H, wavelength l = 2p/|k|
and circle frequency w that propagates in k direction writes and
looks as shown below. |
| |
| E(r,t); H(r,t)
|
= E0; H0 · exp{i(kr
–wt)} |
|
 |
|
|
 |
The electric or magnetic field are vector quantities,
always perpendicular to each other. Light thus always has a polarization vector
associated with it, defined as the direction of the electric field vector (always perpendicular to the propagation direction). |
 |
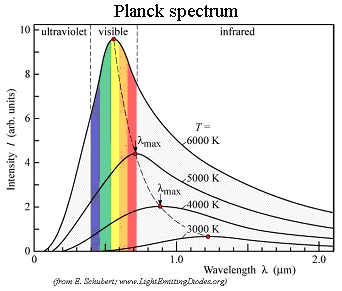
Where does light come from? The sun, of course, is a major producer of light and so is any
other hot body. Max Planck, as you know, first described the spectrum
of light emitted by a hot "black body" in his famous work that was the
beginning of quantum theory. The link gives a short
and simple derivation |
|
 |
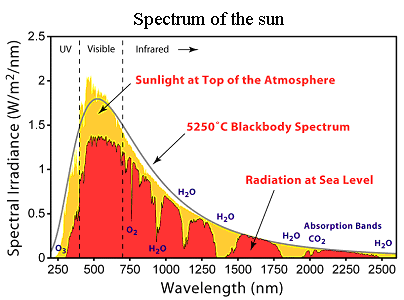
What Planck calculated and what the sun actually does is shown in the following
pictures. |
| |
|
|
 |
The sun comes pretty close to a black-body spectrum and the same is true for a light bulb
or any other light source relying on high temperatures. |
|
 |
It is clear to a Materials Scientist or Engineer that the sun is hot because nuclear fusion
going on in its interior delivers the necessary energy, and that the radiation energy flooding the earth is the one and
only energy on which life depends. |
|
 |
Right now (2011) we enter the age of massive solar energy harvesting via solar cells and wind or water power. The necessary materials science
and engineering for doing this on a large scale will provide work and jobs for many years to come - but that will not concern
us here. |
 |
Besides hot bodies we also have "cold" light sources like light emitting diodes (LEDs) and Lasers. We will come
to that later in more detail. |
 |
Most light sources and all hot bodies produce incoherent light
(travelling in all directions with random phases) and multi-chromatic light (having
all kinds of frequencies), which is a far cry from the E = E0
· exp(ikr) fully coherent and mono-chromatic plane wave that we like to use as mathematical
representation. Sun light or artificial light sources used for illumination thus generate extremely "messy" light
from a purists viewpoint. The messy light is nevertheless quite important in a general sense (imagine it missing!) but not
of much technical interest - besides generating it.
Laser light, by contrast, is
a good approximation to the plane wave model but not of much use for illuminating your kitchen. |
|  |
What we are interested in here is working with light. That means we
have to consider manipulating it by running it through or off materials. What comes
to mind in this context are optical products and components. The table below gives
an incomplete list of a few catchwords that you should know in this context |
|
|
| Products and components around light technology |
| Components |
Products | Field |
| Lenses (and apertures) |
Microscope, Glasses, Camera, Film projector | Geometric optics
| | Mirrors |
Reflector telescope; steppers, optical MEMS |
| Prisms | Binocular; Reflectors |
| Filters | Color photography etc. |
| Diffraction gratings | Spectrometer |
ß |
| Anti reflection coatings | Solar cells, glasses, lenses |
| Linear polarizers |
Cameras, sun glasses, optical measurements, | |
| Circular polarizers | 3-D cinema, advaned measurements |
"Tensor" Optics
Interference Optics |
| Interference filters; Interferometers |
Optical precision measurements |
| Phase shifters, High resolution optics |
Lithography for Microelectronics |
| "Digital" optics |
Beamers, Displays, Cameras, optical MEMS |
| Faraday, Kerr, Pockel, ... effects |
LCD display, ultrafast modulation, advanced analytics |
| Optical fibers | Optical communication, sensors |
| LED, OLED, Lasers |
High efficiency light sources, Displays, Processing, .. |
ß |
| Non-linear materials | Frequency doubling |
| Photonic crystals | "Optical" semiconductors |
Quantum Optics | | Quantum dots |
Optical computing |
|
 |
The message is loud and clear. We have to move from simple geometric
optics to "tensor" optics and interference
optics, arriving finally at quantum optics. We keep in mind, however, that there
is only one kind of optics - those catchwords do not describe different optic realities
but just different approaches to one and the same thing. |
| |
|
© H. Föll (Advanced Materials B, part 1 - script)