5.1.4 Energy Flow, Poynting Vector and Polarization

Energy Flow and Poynting Vector

Light as a wave, by definition, is polarized since an arbitrary light wave can always be decomposed into plane waves described by the electrical field vector E(r,t)=E₀exp{i(kr –wt)} and the corresponding expression for the magnetic field.

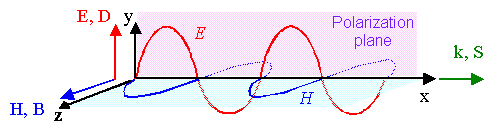
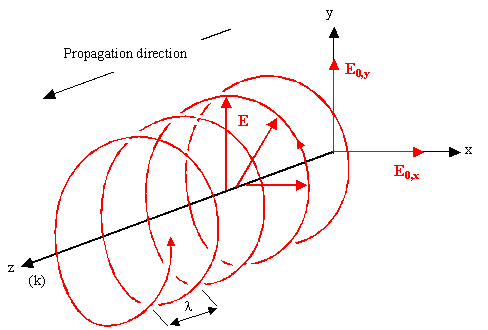
The electrical field vector (or the electrical displacement vector D in material) thus is contained in some plane (the polarization plane) that contains the direction of propagation (direction of k-vector). Looking for example at a picture we had before but now augmented with the relevant vector quantities, we see that in this case:

Polarization plane=(y,x) plane.
Propagation direction=k direction=Poynting vector S direction=x direction here.
E-field amplitude in y-direction given by E₀.
H-field amplitude in z-direction given by H₀.

E_y(t)	= E_y0 · exp{i(kx – wt)}
H_z(t)	= H_z0 · exp{i(kx – wt)}

This all looks well-known and clear. Usually we don't bother to go much deeper at this point. In a Master study course, however, you now ponder the picture and the equations above for a while. Then a few questions should come up, for example:

Can polarization be described by a vector? Could I just use a unit vector in E₀-direction?
What happens if E₀; H₀ are not parallel to D₀; B₀, something to be expected in anisotropic materials?
How do I describe polarization in the particle picture?
Is the electrical and magnetic field really in phase as shown above?
How large, in V/cm, is the electrical field E₀ in a typical light wave. How large (roughly) is it for one photon of a given energy?
Let's assume you know the electrical field E₀: how large is the magnetic field H₀ associated with it?
The energy a photon brings along is E_Ph=hn. How is this light energy transported by an electromagnetic wave?

It's not very difficult to conceive and to understand these questions. How about the answers?

The bad news is: There are no easy answers for some of those questions.

The good news is: For most of what follows you don't have to worry about the answers. I will go into details later whenever necessary. For now you can use this link to get some ideas about the answers and, even better, you could do the simple but illuminating exercise below.

Let's start with the last question. Light flow equals energy flow. All of us who once experienced a sun burn (or shot down one of those evil alien space ships with a Laser gun) know that. How does light energy "flow" exactly?

Well, we (should) know how much energy density W =energy /cm³ is contained in an electric or magnetic field in vacuum (in materials use D and B instead of E and H): We have:

W_elect	=		e₀ · E² 2

W_mag	=		m₀ · H² 2

[W_{elect; magn}]	=		[Ws m^–3]

We do not yet know, how E and H are linked. All we need to know is that this follows "straight" from the Maxwell equations and is given by

E₀	=		æ ç è	m_rm₀ e_re₀	ö ÷ ø	½	· H₀	=	Z_w· H₀

We defined a new quantity Z_w=E₀/H₀=(m₀m_r/e₀e_r)^½ that is called the wave impedance of the medium. This is an apt name since Z_w does have the dimension "Ohm" (W) as required for an impedance.

For the vacuum impedance (e_r, m_r=1) we get

Z_w(Vacuum)=376,7 W

This is a bit strange if you think about it. We just connected vacuum, the nothing, with a defined property that can be expressed in a simple number! You can buy a resistor with 377 W and wonder why it somehow reflects a property of vacuum.

Be that as it may, we now define a new vector S as follows:

S	=		E × H

	=		Poynting vector

The Poynting vector has interesting properties:

S points in the direction of the propagation of the light, i.e. in wavevector k direction as shown in the figure above.
|S|=S=E₀ · H₀ · cos²(kr - wt), the magnitude of the Poynting vector, gives directly the power flux in W/cm² of an electromagnetic wave
The average power delivered to an area is thus .

<S>	=	E₀H₀ 2	=	E₀² Z_w	= E₀² ·	æ ç è	e_re₀ m_rm₀	ö ÷ ø	½

<S>	µ	E₀² · e_r^½	µ	E₀² · n

Don't mix up the power flux in W/cm² with the specific energy measured in in Ws/cm³or J/cm³ that is contained in fields as shown above! It's time for an exercise to get some ideas about the numbers associated with light power and field strength!

Exercise 5.1.2
Energy, field strength and photons

We still have a bunch of open questions from above but before we tackle those we have to learn a bit about polarization.

Polarization of Light

It is clear that an idealized plane wave, given essentially by the exp[i(kr – wt)] term, describes a monochromatic and fully coherent light wave propagating in exactly one direction that is also linearly polarized by definition.

Some Laser beams may come close to emitting a plane wave matching that description but laser light is a far cry from "normal" light.

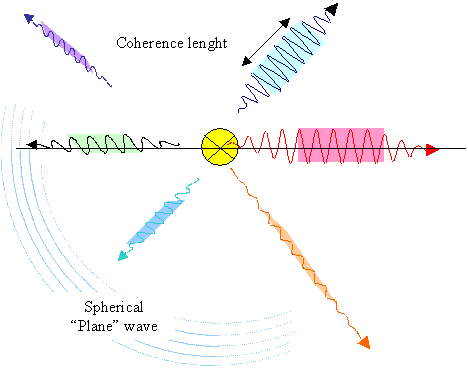
Most real or normal light beams, e.g. the light "beams" emanating from light bulbs, are not polarized as we know. "Real" light from light bulb looks - very schematically - as shown below. We are forced to assume that the electromagnetic wave has a beginning in space and time (at the light bulb, like now) and an end. The length of the whole thing we call "coherence length". The color (=wavelength), and the polarization plane for one of those waves with a beginning and an end, has some fixed value but that is different from the next wave coming along. The distribution of wavelengths we call the spectrum of the light source, and the distribution of polarization planes will be random. Each ones of theses "wavelets" is caused by an electron changing its state from higher to lower energy.

The picture might be interpreted as photons coming out of the light bulb. If one of those wavelets would be seen as a completely abstract symbol for a photon, this would be true. However. photons are not just short pieces of an electromagnetic wave, so one must not interpret this figure as a picture of photons.

We have a number of new questions to consider (never mind that we did not answer all the old ones yet):

How do we detect if and in which direction a light beam is polarized?
How can we polarize an unpolarized light beam if the need arises?
Does is matter if and how a light beam is polarized for the applications we have in mind?
If it matters: how do we optimize the needed polarization?
How does the polarization of a wave relate to photon properties?
Are there other polarization modes besides linear polarization?

We are now at the point where serious optics starts.
It ain't exactly easy but we will only scratch the surface here.

Let's look at these questions one by one. We will encounter rather difficult topics that we only treat in a perfunctory way here. Some topics will come up later again.

1. How do we detect if and how a light beam is polarized?

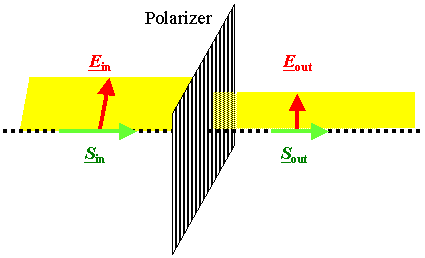
By using a polarizer, i.e. some material that transmits only that E-field component of an incoming light beam that is parallel to some material specific polarization direction as shown below.

From Rogilbert; French Wikipedia

Turn your polarizer and the light intensity coming out stays either constant if the incoming beam is not polarized at all (but is always lower in intensity) or varies between zero and maximum (=incoming) intensity in a cos² fashion if the incoming beam is 100 % linearly polarized, as shown above. If the beam is partially polarized you have a mix of the two extremes.

The second question (2. How can we polarize an unpolarized light beam if the need arises?) is answered too: Use a polarizer! Of course we have a new question now, the really tough one.

7. What, exactly, gives a material polarizing properties?
And how can I manipulate or engineer those properties? That's indeed a tough question as we shall see in one of the next sub chapters. Before we try to answer this one, we look at a few simple things first.

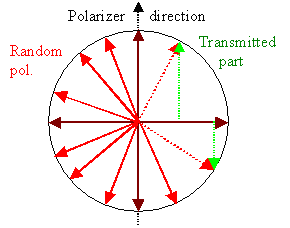
What we perceive now is that a standard non-polarized light beam simply consists of many intrinsically polarized beams but with randomly distributed polarization directions. The total polarization effect then is zero.

This is easy to perceive with the help of the figure on the left.

Randomly distributed polarization vectors sum up to zero=no polarization.

Note that we now indirectly answered one of the earlier questions from above: Yes, you can use a polarization vector like we do in this case and most others. But beware! Polarization in general is more tricky than you might think and a simple vector is not always enough to describe it mathematically. (Remember the problems encountered in using a polar vector for describing rotations?). You will need a matrix if you go about it systematically.

The picture also makes clear why the polarized beam emerging from a polarizer has a lower intensity than the incoming beam, and also how much lower it will be.

If we want to make life easier we can replace a large number of beams with random polarization directions (red vectors) by just two beams at right angles (brown vectors).

It is time for a quick exercise:

Exercise 5.1.3
Polarization

3. Does is matter if and how a light beam is polarized for the applications we have in mind?

The answer is simple: No, it does not matter for many simple or standard applications. Your glasses, binoculars, microscopes, and so on, work perfectly well with "normal" light. With a polarization filter your camera will make somewhat better pictures in certain circumstances but that is usually not decisive.

However, for anything a bit more sophisticated, like all the optical things that a Material Scientist and Engineer needs for her or his work or develops for others, it will matter very much as we will see. Here is a table that should give you some idea:

Application	Polarization matters a lot	Polarization doesn't matter much
Simple optical instruments (Cameras, binoculars, ...)		Forget it
Better optical instruments (Cameras, ..	you use a "Pol filter"
Optical communications	not yet but soon	most cases now
Optical measurements	most depend on polarization
3-dim movies	including circular polarization
Laser	in many cases	some cases
LCD displays	impossible without polarization

4. If it matters: how do we optimize the needed polarization?

The answer is simple again: by constantly coming up with new or improved materials. Note the extremely simple and important truth:

If a light beam does not interact with some material,
its properties will not change.

5. How does the polarization of a wave relate to photon properties?

Well - the photon has a spin of 1/2! Naively put, there is a kind of (polar) vector associated with it. So there might be a relation between polarization and spin?

Yes - up to a point. But it's not that simple! Whatever the case may be, my advice is: forget it! Whenever polarization comes up, only think in the wave picture. Otherwise you simply run into all kinds of unnecessary problems. However, it is perfectly possible to describe all the effects of polarization in the particle picture, too. There is no contradiction.

We have the last questions to consider and that will open a large can of worms, as the saying goes. Let's start with No. 6: Are there other polarization modes besides linear polarization?

Yes there are. They are called circular and elliptical polarization. Here we go:

Other Modes of Polarization

Some idealized plane wave travelling in z direction with the electrical field vector pointing in x-direction writes as E_x(z,t)=E_{0,
x}exp{i(kz –wt) for the the electric field part. This idealized light wave is a solution of the Maxwell equations for some (idealized) conditions.

E_y(z,t)=E_{0, y}exp{i(kz –wt + p/2); i.e. the same wave but with the electrical field pointing in y-direction and a phase difference of p/2 (or any other you care to insert) is also a solution, of course.

If those waves travel inside a material, all we have to do is to replace the electrical field E by D, the dielectric displacement (and H by B, of course), and to take care of the change in wavelength or the magnitude of k, respectively.

If the material is isotropic and linear, we have D=e₀e_rE. That means that not only the two waves from above are still a solution of the Maxwell equations for the case considered, so is any superposition of those (and possibly other) solutions. So whatever we are about to discuss works just as well in "simple" materials. Most optical materials are amorphous (called "glass"), and meet the requirement isotropic and linear in a fair approximation so we don't have to worry yet.

However, many crystalline materials are neither isotropic nor linear - and then we will be in trouble. Those materials are of course very interesting to a Materials Scientist but the theory of what happens is difficult and we will deal with that later.

Now let's add up the two E (or D) solutions from above and see what we get.

E_x(z,t) + E_y(z,t)	=		E_{0, x}exp{i(kz –wt)	+	E_{0, y}exp{i(kz –wt+ p/2)

The real part of this complex equation gives the electrical field vector, we have

E	=		E_{0, x} · cos(kz –wt) + E_{0, y} · sin(kz –wt)

The full electrical field E thus is obtained by adding two vectors at right angles with magnitudes that change sinusoidally between (±E₀). The total effect is a vector with length E₀ that rotates with a circle frequency w around the z-axis.

What you get is called circular polarization for obvious reasons; it looks like shown below. Note that all of this appears to be far more complicated than it actually is, this is made clear by the animation below which shows the basic simplicity of what is going on.

(From wikipedia)

You realize, if you think about it, that we just opened the promised rather large can of worms. We started with simple, intuitively clear linear polarization and now progressed to circular polarization by superimposing two special linearly polarized waves. Of course, we can produce two basic kinds of circular polarization: left-handed and right-handed circular polarized light this way. Equally of course, we can now superimpose all kinds of waves with all kinds of phases. Where will it end?

Actually, it's not as bad as it might be. Superimposing whatever you like just gives you elliptically polarized light (plus, perhaps, a background of unpolarized light).

The extremes of an ellipse are straight lines (linearly polarized light, just superimpose the two waves without a phase difference) and the circle (phase difference p/2; equal amplitudes).

We will stop at this point. Far more important than going into intricate details of all this polarization stuff is to consider:

Question 2 from above, not yet addressed: How do we make all these kinds of polarization? (Answer: with special materials, of course).
What is it good for? Who needs circular or elliptically polarized light? (Answer: you - if you watch, e.g., 3D-movies)

We will look very briefly at some answers in the next chapter, where we deal with light and materials.

Questionaire
Multiple Choice questions to 5.1.4