|
Know your numbers and relations for visible light! |
|
For the propagation of light:
use the wave model
For the generation and
disappearance (= absorption) of light:
use the photon model
|
Snellius law:
n = sina/sinb with a,
b the angle of incidence
or propagation, resp. |
|
|
 |
Wavelengths: l
» 400 nm - 800 nm. | |
| |
lmat = l0/n. |
|
|
 |
Frequency: n» 10 15
Hz. | |
|
 |
Index of refraction: n = er½
» 1,5 - 2,5 | |
|
 |
Energy E » 1,8 eV - 3,2 eV. |
|
|
 |
Dispersion relation: c0 = n l0 = 3 ·
108 m/s
cMat = n l0/n(l) |
|
| |
| |
| |
 |
Know yout basic equations and terminology |
|
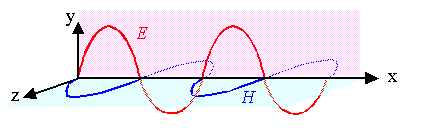 |
Coherent monochromatic plane wave
E and H perpendicular and in phase |
|
| | |
| |
| | |
E(r,t)
H(r,t) | = |
E0
H0 |
· exp{i(kr –wt)}
|
|
| |
| |
| |
|
|
 |
Reflection always with "angle in" =
"angle out".
| |
|
 |
Refraction is the sudden "bending" or "flexing"
of light beams at the interface | |
|
 |
Diffraction is the continous "bending" of light beams around corners;
interference effects. | |
| | |
| |
|
 |
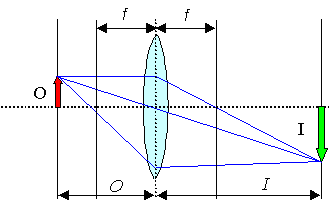
Geometric optics
Key paramters |
|
|
|
 |
Focal length f and
numerical aperture NA of lenses,
mirrors. | |
|
 |
Image formation by simple geometric constration |
|
|
 |
Various aberrations (spherical. chromatic, astigmatism, coma, ...) limit performance. |
|
|
| |
| |
 |
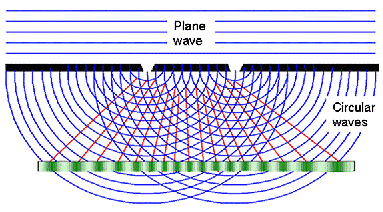
Wave optics
Huygens principle: and interference |
|
|
|
 |
Ultimate limit to resolution | |
| | |
| |
| | |
| |
| |
| |
|
 |
Know your basic types of waves: |
|
|
 |
(Running, coherent, monochromatic) plane wave.
| |
|
 |
Standing waves = superposition of plane waves. |
|
|
 |
Incoherent, multichromatic real waves |
|
| |
| |
 |
Relation s between electrical field E, magnetic field H
and Poynting vector (energy flow vector) S = E × H |
|
|
|
|
| [Welect; magn] |
= |
[Ws m–3] |
|
| E0 |
= |
æ
ç
è
|
mrm0
ere0 |
ö
÷
ø |
½ |
· H0 |
= |
Zw · H0 |
|
|
| |
| |
| |
| |
| |
| |
|
|
|
This equation links energy flow (easy in photon picture)
to field strength in wave picture. |
|
|
 |
Zw = wave impedance of the medium.
Zw(vacuum) = 376,7 W |
|
| |
| |
| |
 |
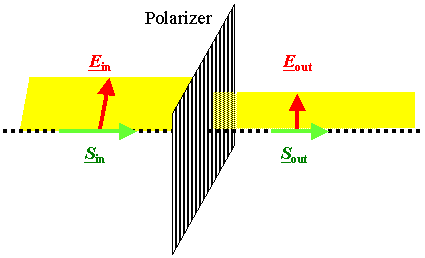
Polarization = key to "advanced" optics.
Simple case: linear
polarization. | |
|
|
 |
Plane of polarization contains E-vector and S (k)
vector. | |
|
 |
Any (coherent) wave is polarized but net polarization
of many waves with random polarization is zero! | |
|
 |
Light intensity (µ
E2) between polarizers at angle a scales with (cosa)2. | |
 |
General case: elliptical polarization; important
are the two extremes: linear and circular polarization. |
|
|
 |
For circular polarizaiton the E-vector rotates on a circle while moving
"forward". This results from a superposition of two plane waves with E-vectors ar right angles
and a phase difference of p/2. |
|
|
 |
Technically important (3-dim Cinema; Lab optics) |
|
|
|
|
© H. Föll (Advanced Materials B, part 1 - script)