5.2 Optics and Materials

5.2.1 Interaction between Light and Matter

The Task

We have a (monochromatic, coherent, polarized) light beam (a plane wave in other words) and a piece of material. We direct our idealized "perfect" beam on the material and ask ourselves: what is going to happen?
First we have to discuss the properties of the material a bit more. It might be:
  • Optically fully transparent for all visible wavelength (like diamond or glass ) or optically opaque (like metals).
  • Optically partially transparent only for parts of the visible wavelength (like GaP or all semiconductors with bandgaps in the visible energy range) or colored glass.
  • Opaque and black (= fully absorbing) like soot or highly reflective (like a mirror).
  • Perfectly flat (like a polished Si wafer) or rough (like paper).
  • Uniform / homogeneous (like glass or water) or non-uniform (like milk: fat droplets in water).
  • Isotropic (like glass) or anisotropic (like all non-cubic crystals).
  • Large (like anyything you can see) or small (like the Au nanoparticles in old church window that produce the red color).
I'm not sure I have exhausted the list. Be glad now that for the time being we look at a simple and "perfect" light beam and not at real light.falling on a real material.
So we have a tall task before us. We first make it a bit easier by considering only flat, uniform, isotropic and transparent materials like glass or (transparent) cubic single crystals like diamond.
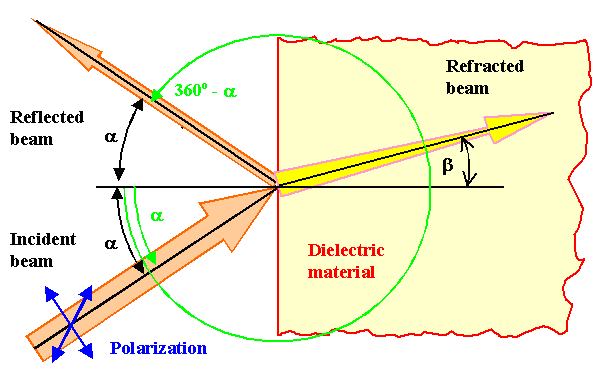
All that can happen for these rather ideal conditions is shown in the following picture:
Basic interaction of light and matter
In essence we have an incoming beam, a reflected beam and a diffracted beam that "goes" into the material.
The incident "perfect" beam must have some kind of polarization. Even if it is unpolarized we should from now on think of it as consisting of two linearly polarized parallel beams with equal intensity and polarization directions differing by 90o. Same thing for the two other beams. Consider them to be two beams with a 90o difference in polarization direction. This is important!
We must expect that the reflected and diffracted or transmitted beams might be polarized, too, but we must not assume that their polarization is the same as that of the incoming beams. We deal with that in the next sub chapter.
The situation in the picture above is very slightly simplified because we don't consider so-called "evanescent waves" at the interface, and we only discuss a linear system - the frequency of the light doesn't change. There are no beams with doubled frequency, for example (can happen in some crystals).
What do we know about the three (times two) light beams shown?
I'll drop the plural from now on. But remember: think of all beams as consisting of two linearly polarized parallel beams with equal intensity and polarization directions differing by 90o.
Incoming beam. We know all about the incident beam because we "make" it. In the simplest case it's a plane wave with an electrical field given by E = E0expi(kin · r  – wt) or, if you prefer, E = E0cos(kin · r  – wt). The basic parameters of the incident beam are:
  • Intensity: We can describe the intensity Iin by looking at E02, the square of the electrical field strength amplitude. In the particle picture it would be the number of photons per second. In regular or technical optics, we have special units, "invented" for dealing with light but we will not cover that here.
  • Frequency: We assume monochromatic light with the circle frequency w.
  • Polarization: We assume some arbitrary constant polarization (= direction of the E vector). By definition, the polarization direction is perpendicular to the direction of the wave vector k. We have only one beam now (the intensity of the second one is zero).
  • Phase: We can pick any initial phase since it's numerical value depends on the (arbitrary) zero point of the coordinate system chosen.
    Note that by just picking a direction (like this — ), you have not yet decided where the tip of the vector is (—> or <—), so we must pick that too. Switching to the other direction then implies a phase change of 1800 or p or reversing the sign of E.
  • Coherence: We always assume full coherence, i.e. there is only one phase. An incoherent beam, for comparison, would be a mixture of beams like "our" beam but with different (= random) phases.
Since we assume a linear system, we can always discuss "colored" light by discussing each frequency separately. We also can deal with arbitrary polarizations by decomposing it into the two basic polarizations considered below which we need to discuss separately. An arbitrary polarization then is just a superposition of the two basic cases; we are back to our "two beam" picture from above.
Reflected beam:. The reflected beam will essentially be identical to the incoming beam except for
  • Intensity: The intensity Iref will be different from that of the incoming beam; we have 0 < Ire < Iin.
  • Direction: We know that we have a mirror situation i.e. aout = ain. Note that its actually aout = 360o –ain if you measure the angles in one coordinate system. Why we know that we have a mirror situation is actually a tricky question!
  • Phase: We might have to consider that the phase of the reflected beam changes at the surface of the material.
Refracted beam: The refracted or transmitted beam runs through the material. We know that there is always some attenuation, damping, extinction or what ever you like to call it. I will call it attenuation. What do we have to consider?
  • Intensity: We know from energy conservation that Itr(z = 0) = Iin – Ire.
  • Attenuation: We expect exponential attenuation according to Itr(z) = Itr(z = 0) · exp–z/aab if we put the z-direction in the direction of the transmitted beam for simplicity. The quantity aab obviously is an absorption length, giving directly the distance after which the intensity decreased to 1/e or to about 1/3.
  • Direction: Snellius law applies, i.e. sina/sinb = n. We also know that the index of refraction n is given by er, the "dielectric constant"; we have n = (er)½.
  • Phase: We might have to consider that the phase of the transmitted beam changes at the interface of the material.
While we seem to know a lot already, some tough questions remain, essentially relating to intensities, phases and attenuation as a function of the polarization, the angle of incidence, and the properties of the material.
As it will turn out, dealing with attenuation is easy. All we have to do is to remember that we replaced the simple "dielectric constant" er some time ago by a complex dielectric function e(w) = e'(w) + e''(w). Since the index of refraction is simply given by the square root of the dielectric constant, we might expect that the dielectric function not only contains the index of refraction but additional information concerning attenuation. We will look at that in sub-chapter 5.2.3 in more detail.
The questions relating to intensities and phases will not go away that easily, however. We will see how to find answers in the next sub-chapter.
   
Finding the Answers
   
How to we have to proceed in order to find answers to the questions raised above? In other words, how can we derive the so-called Fresnel equations that contain the answers?
First we need to look a bit more closely at the polarization. Remembering our old convention is helpful:
Polarization (if not otherwise stated) is always
taken in the E-field direction.
As long as we only deal with linear polarization, meaning that the polarization direction is always the same (i.e. not a function of time), we can describe any wave with some or none polarization by a superposition of the two waves discussed above with two orthogonal polarization directions.
We now need to define one of the two polarizations directions. The other one then follows automatically. We use the following convention like everybody else:
TE polarization:
("Transversal electric") 		 TM polarization:
("Transversal magnetic") 
E lies perpendicular to the (blue) plane of incidence defined by the normal vector n of the material surface considered and the wave vector kin of the incoming wave.
E thus lies in the surface of the material. Also described as _|_ (perpendicular) case because the E-vector is perpendicular to the "plane of incidence".
The magnetic field vector H then lies in the "plane of incidence".		 E lies in the (yellow) plane of incidence defined by the normal vector n of the material surface considered and the wave vector kin of the incoming wave.
E then has no components in the material surface. Also described as || (parallel) case because the E-vector is in the "plane of incidence".
The magnetic field vector H then lies in in the surface of the material.
Once more: Arbitrary (linear) polarizations can always be described by a suitable superposition of these two basic case.
Energy conservation gives us a simple and obvious relation for the energies or intensities flowing along with the waves:
Itr(z = 0)  =   Iin – Ire
Note in this context that the energy of a electromagnetic wave with electrical field amplitude E0 traveling in a medium with dielectric constant e is proportional to e½(E0)2 as we have figured out before. Note also that the transmitted beam might be attenuated so its energy is eventually transferred to the medium it's traveling in.
Going beyond that, however, needs some work. We must, in essence, start with the Maxwell equations, look at the "electromagnetic wave" case and solve them for the proper boundary conditions at the boundary of the two media.
Or do we? Actually, we don't have to - as long as we remember (or accept) that there are simple boundary conditions for all the fields coming up in electromagnetism as illustrated below:
Boundary conditions for E and D
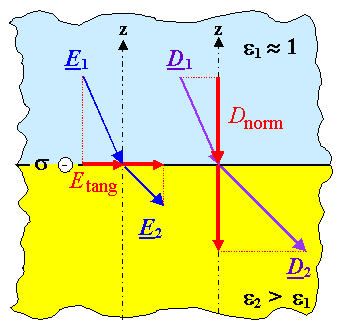Electrical field E     Etang = const
     
Dielectric displacement
D = e0erE		    Dnorm = const.
 
Magnetic field H    Htang = const
     
Magnetic induction
B = m0mrE		   Bnorm = const
The picture shows some interface between two (dielectric) materials. In the picture the first one is something like air or vacuum (er » 1) but the relations holds for all possible combinations. How do we derive the boundary conditions?
It's easy. For an electrical field you need a gradient in some charges. For a change of an electrical field vector you need an additional charge gradient right at the place where the field vector is supposed to change. In the above case, for a change on the tangential component you would need a lateral gradient in the charge distribution on the surface.
If you understood chapter 3, you know that some surface charge with an area charge density s is generated by polarization. Looking long enough at Gauss' law will show that a lateral charge gradient cannot exits. The tangential components Etang of E therefore must not change going across the boundary. The normal component, in contrast, must change because we do have an addition charge gradient perpendicular to the surface.
Using related arguments makes clear that for the dielectric displacement D the normal component must remain constant. For the magnetic field H and the magnetic flux density or induction B corresponding relations apply. You might reason that this provides the definition of D and B. It's just extremely useful to have vectors meeting those boundary conditions.
Fortified with these boundary conditions, valid for any fields including the rapidly oscillating electric and magnetic fields of light, the derivation of the Fresnel equations - that's what we are after - is not too difficult as we will see in the next sub-chapter.
   
Questionnaire
Multiple Choice questions to 5.2.1
With frame Back Forward as PDF

© H. Föll (Advanced Materials B, part 1 - script)