|
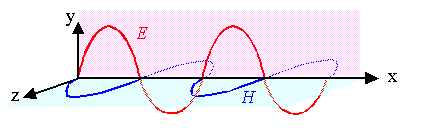
1. Is the electrical and magnetic field really in phase as shown in the drawing above? |
 |
Yes it is - all serious sources agree even so the reasons given are mostly not obvious. The
real question, of course, is: why should this be a question at all? |
|
 |
Solving the Maxwell equations quite generally for the "wave" case, simply
gives solutions with no phase differences of the form: |
| |
| E(r,t); H(r,t)
|
= E0; H0 · exp{i(kr
–wt)} |
|
|
 |
True enough. But this simple solution describes an infinitely
extended electromagnetic plane wave—something that does not exist. So let's look
what happens for finite waves that have a beginning at some point in space. |
|
 |
Not so easy for light. The generation of a photon is always a quantum mechanical effect not
covered by the Maxwell equations. However, the equation above is valid for all electromagnetic
waves. It is also valid, e.g. for the radio waves produced by a simple dipole antenna
and this is covered by the Maxwell equations. We thus can look at the generation of a radio wave instead of a light wave;
something easier to conceive than the generation of a light wave by the transition of an electron from one energy level
to another one. |
|
 |
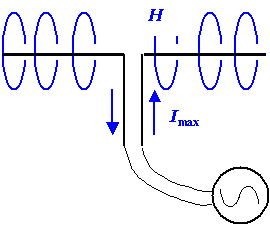
The figure below shows the principle. An AC current is fed to a dipole, it drives charges
to the two ends. Maximum current flows when there are no charges at the dipole ends, we then have maximum magnetic fields
and no electric field |
|
 |
The charges transported to the end of the dipole cause an electrical field that opposes current
flow. Eventually, at maximum charge and thus electrical field, current flow is zero and there is no magnetic field. |
| |
|
|
 |
The unavoidable conclusion is that at the place where we make
the wave - and it doesn't matter what kind of wavelength you envision - the electrical field and the magnetic field are
90o out of phase! |
 |
Now we have a problem: far away from the "light source" the two fields are in phase but where we make them they are out of phase! |
|
 |
The problem is solved when one looks at the full set of equations (not easy). Far away from
the dipole, in the far field, we "see" a point source that emits a spherical wave
and there is no phase difference, indeed. Close to the dipole (measured in units of the wavelength), in the near field, we do not see a point source but a complex geometry as
sketched above. The fields in the near field do not have spherical symmetry and phases right at the dipole are different
by 90o, indeed. |
|
 |
In mathematical terms, we superimpose a complicated near field term with a general 1/rn
dependence (n > 1 on a simple spherical wave. The near-field term dominates close to the antenna. Since it decreases
faster than the spherical wave term, for large distances we can neglect the near-field term and are left with a spherical
wave that appears to be a plane wave if you only look in parts of space. |
 |
You don't need to know this but you should be aware that as soon as you leave the ideal realm
of the simple plane wave without a beginning and an end, things tend to get much more
complicated. But things also tend to be much more like what we actually know. |
|
© H. Föll (Advanced Materials B, part 1 - script)