|
Als wir uns im Zusammenhang mit "Random
Walk" mit Besoffenen beschäftigt haben, kam der Begriff der Lebensdauer
zum erstem Mal hoch. |
|
 |
Das war die Zeit, die zwischen Beginn des "random walk" lag (Start = Generation des statistisch herumirrenden Teilchens; z. B. Verlassen der
Kneipe) und dem Ende (z. B. durch Aufgelesen werden von der Polizei). Das setzen wir jetzt um auf unsere Elektronen und
Löcher. |
|
 |
Dazu haben wir zunächst den Elementarprozeß der Erzeugung oder der Generation eines Elektron-Loch-Paares, der darauf folgenden Wanderung durch das Kirstallgitter
und der dann nach einer (mittleren) Zeit t, die wir Lebensdauer
genannt haben, erfolgenden Wiedervereinigung von Loch und Elektron; einen Prozeß, den wir Rekombination nennen. |
|
 |
Generation und Rekombination
sind neben der Dotierung der Schlüssel zur Halbleiterphysik und -technik; wir müssen
uns damit befassen. |
 |
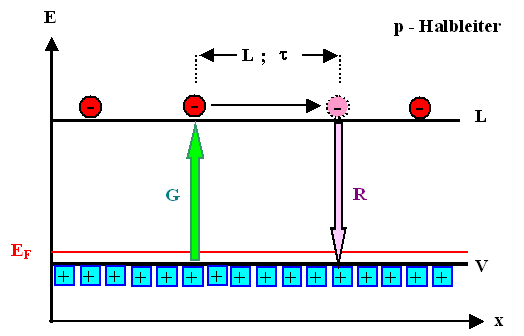
Wir betrachten das mal im Banddiagramm. Wir führen dazu eine Bildbetrachtung
durch und interpretieren den unten gezeigten Lebenslauf einer Minorität in einem p-Typ-Halbleiter. |
| |
|
 |
Aus einer eingehenden Kontemplation dieses Bildes lassen sich folgende Schlußfolgerungen
ziehen: |
|
 |
1. Es enthält redundante Information. Sowohl
die Lage der Fermienergie als auch die symbolisch eingezeichneten Majoritätsladungsträger "Löcher"
als auch die Beschriftung sagen alle dasselbe: Wir haben einen p-Typ-Halbleiter vor
uns. |
|
 |
2. Das Verhältnis Majoritäten : Minoritäten ist ungefähr 4 :
1. Damit hätten wir nur eine sehr schwache Dotierung. Es liegt damit nahe, daß der Künstler die Zahl
der Löcher und Elektronen symbolisch meint. Denn ein realistisches Verhältnis
von z. B. 1.000.000 : 1 ist in dieser Kunstform offenbar nicht darstellbar. |
|
 |
3. Im linken Bereich ist ein Generationsereignis
zu sehen. Während der neu erzeugte Minoritätsladungsträger – das Elektron
– eindeutig zu identifizieren ist, bleibt der zugehörige Majoritätsladungsträger "Loch" anonym,
er ist in der Masse der anderen Löcher nicht zu identifizieren. Der Künstler will wohl einen Hinweis darauf geben,
daß sich bei der Generation eines Ladungsträgerpaars bei den Majoritäten
so gut wie nichts ändert, während bei den Minoritäten
die Änderungen deutlich spürbar sind. |
|
 |
4. Im Zentrum des Bildes folgen wir dem Schicksal des frisch generierten Minoritätsladungsträger. Nachdem er sich eine Länge L von seinem
Geburtsort entfernt hat, geht er durch Rekombination wieder ins Nirwana ein –
das Elektron ist (im Leitungsband) spurlos weg. Wiederum fehlt jeder Hinweis auf den Rekombinationspartner aus der Masse
der Löcher. Darüber hinaus ist der dreidimensionale "random walk" in minimalistischen Manier auf einen
Pfeil reduziert. |
|
 |
5. Es läßt sich noch ein letzter Hinweis auf die Vorgänge in und zwischen
den Bändern finden: Alle Minoritäten (und auch die Majoritäten) sind
sich völlig gleich – wir sehen rote Kreise, die für sich genommen völlig ununterscheidbar sind. |
 |
Soviel Information steckt in einem simplen Banddiagramm – man muß
sie nur zu interpretieren wissen! Nüchtern betrachtet, nehmen wir jetzt folgende Punkte zur Kenntnis: |
|
 |
1. Ganz offensichtlich ist das, was sich bei den Minoritäten
abspielt, viel wichtiger als die Vorgänge bei den Majoritäten. Denn jede Änderung bei Ladungsträgerkonzentrationen
bewirkt bei den Minoritäten immer sehr viel größere Abweichungen vom Gleichgewicht als bei den Majoritäten.
Und es sind immer die Abweichung vom Gleichgewicht, die Reaktionen aller Art antreiben! |
|
 |
2. Obwohl wir bisher immer nur einen
Generationsvorgang mit anschließender Rekombination betrachtet haben, sollte uns doch klar sein, daß, wenn
ein wie auch immer generiertes Elektron nach einer Zeit t
rekombiniert, solches dann notwendigerweise analog für alle Elektronen gilt! Denn
alle Elektronen sind gleich und keine sind gleicher! |
 |
Damit würden praktisch alle
Minoritätsladungsträger nach ein paar Lebensdauern t verschwunden sein
(denn die "Abbaurate" folgt natürlich dem allgemeinen Gesetz zum Zerfall
angeregter Zustände ). Die Rekombinationsrate
R,
d.h. die Zahl der pro Sekunde (und cm –3) rekombinierenden Minoritätsladungsträger, ist
damit einfach |
| |
|
|
 |
Zeit für eine kleine Übung. |
 |
Da aber im
Gleichgewicht die Konzentration aller Ladungsträger konstant ist, können wir eine erste, sehr wichtige
Schlußfolgerung ziehen: |
|
 |
Im Gleichgewicht ist die Generationsrate
G, d.h.
die Zahl der pro Sekunde (und cm –3) generierten Minoritätsladungsträger, genau gleich
groß wie die Rekombinationsrate, d.h. |
| |
|
|
 |
Das läßt sich leicht verstehen: Wenn von einem Bankkonto ein bestimmter Betrag
pro Zeiteinheit abgehoben wird – z.B 1 € pro Tagoder 1 000 000 € pro Tag –, dann wird
der Kontostand (im Mittel) nur dann konstant bleiben (im Mittel), wenn genausoviel Geld pro Zeiteinheit überwiesen
wird. |
|
 |
Das Beispiel paßt genau! Und es sagt uns darüberhinaus ganz plastisch, daß
aus der Größe der Ab- und Zuflüsse kein wie auch immer gearteter Schluß auf den Kontostand
gezogen werden kann, wie auch umgekehrt ein wie auch immer gearteter unveränderter Kontostand nichts über die
Höhe der Zu- und Abflüsse aussagt. |
 |
Damit haben wir im (nur so rumliegenden) Halbleiter nicht nur
ein Gleichgewicht, wir haben immer ein dynamisches
Gleichgewicht. |
|
 |
Jeder Minoritätsladungsträger wird irgendwann (und irgendwo) generiert,
läuft (im Mittel) eine Diffusionslänge durch den Kristall und verschwindet dann wieder durch Rekombination. |
|
 |
Das gilt natürlich im Prinzip auch für die Majoritätsladungsträger. Von
denen ist aber die weitaus überwiegende Anzahl im (dynamischen) Gleichgewicht mit den Dotieratomen,
und die paar, die sich mit Minoritäten abgeben, spielen für die Gesamtanzahl keine Rolle. |
| | |
|
Lebensdauer, Diffusionslänge und Beweglichkeit |
| | |
 |
Schauen wir uns das Ganze noch etwas genauer an. Wir wiederholen obige Aussage
mal etwas ausführlicher: |
|
 |
Jeder Minoritätsladungsträger wird generiert und läuft dann (im
Mittel) eine Diffusionslänge
L durch den Kristall. Dazu braucht er (im Mittel) die Zeit t, die wir ab
jetzt Minoritätsladungsträgerlebensdauer
oder kurz Lebensdauer nennen,
und verschwindet dann wieder durch Rekombination. |
|
 |
Der Zusammenhang zwischen Lebensdauer und Diffusionslänge ist dabei wie bei jedem "Random walk" durch die folgende Beziehung gegeben: |
| |
| L = (D · t)½ = (µkBT/e
· t)½ |
|
|
|
 |
D ist dabei der Diffusionskoeffizient
der Elektronen oder Löcher, den wir über die Einstein-Smoluchowski-Beziehung
auch durch die Beweglichkeit µ ausdrücken können. |
 |
Den Diffusionskoeffizienten
der Elektronen oder Löcher haben wir schon mal kurz
kennengelernt, er ist einfach mit den Stößen und damit mit dem "Random Walk" gekoppelt.
|
|
 |
Da wir µ jetzt kennen, kennen wir jetzt
auch D. Damit können wir bei Kenntnis von L oder
t die jeweils andere Größe berechnen. |
|
 |
Es bleibt noch, eine etwas quantitativere Vorstellung davon zu bekommen, wie groß L
oder t in einem gegebenen Material sein wird. |
 |
Hier kommt jetzt etwas vollständig Neues: Es gibt bezüglich dieser Frage
zwei Sorten von Halbleitern: |
| |
Direkte Halbleiter:
L und t sind klein (ungefähr ns
/ µm)
Bei der Rekombination eines Elektron-Loch-Paares entsteht Licht
mit hn = Eg.
Indirekte Halbleiter:
L und t sind groß und stark defektabhängig
(ungefähr µs...ms
/ 500 µm)
Bei der Rekombination eines Elektron-Loch-Paares entsteht (fast) nur Wärme. |
|
 |
Die gebräuchlichen Halbleiter ordnen sich in diese Schema
(direkt/indirekt) so ein (zur Erbauung mit noch ein paar mehr Daten): |
| Material |
Si | Ge |
GaAs |
InP |
InSb |
GaP |
GaN |
SiC |
Diamant |
| Kristall |
| Kristallstruktur |
Dia-
mant | Dia-
mant |
Dia-
mant | Dia-
mant |
Dia-
mant |
Dia-
mant | Wurtzit
(hex.) |
viele Varianten,
kub./hex./rhomb. |
Dia-
mant |
Gitterkonstante
[nm] |
0,5431 | 0,565 |
0,565 | 0,587 |
0,648 |
0,545 | a=0,319
c=0,518 |
a=0,30
c viele Werte | 0,357 |
| Einige Zahlen zu Ladungsträgern
| | Energielücke [eV] |
1,12 | 0,66 |
1,42 | 1,35 |
0,17 |
2,26 | 3,4 |
2,39–3,26 | 5,47 |
| Typ | indirekt |
indirekt | direkt |
direkt | direkt |
indirekt | direkt |
indirekt |
indirekt |
| Neff in L [1018 cm–3 ] |
28
(32) |
10,4 | 0,47 |
0,54 | 0,042 |
|
| |
| |
Neff in V [1018 cm–3] | 10
(18) | 6 |
7 | 2,9 | |
|
| |
|
| ni [106 cm–3] |
6 600
13.000 |
20.000.000 | 2,2 |
5,7 | |
|
| |
|
Beweglichkeit
(undotiert) [cm2/(Vs)]
µn
µh |
1 500
450 |
1.900
3.900 |
8.500
450 |
5.000
200 |
80.000
1.250 |
300
150 |
|
500–1.000
20–50 |
200–2.200
1.800–2.100 |
Lebensdauer
[µs] |
2500 | |
0,01 | 0,005 |
|
|
|
| |
| Dielektrische Eigenschaften
| | Dielektrizitätskonst. |
11,9 | 16 | 13,1 |
12,4 | 17,7 |
11,1 |
| 9,7–10 |
5,5 |
Durchbruchs-
feldstärke [kV/cm] |
300 | |
350 | 400 |
|
|
|
| |
|
|
 |
Traurig, traurig: Unser Hauptmaterial Si ist für die Optoelektronik
nicht geeignet – es kann kein Licht rauskommen, wenn man Strom durchschickt! |
 |
Die Frage, die sich jetzt aufdrängt, ist klar: Warum, o Herr, hast du zwei Sorten gemacht? |
|
 |
Die Antwort ist einfach, nur die Begründung liegt weit jenseits unserer Möglichkeiten.
Schauen wir uns das obige Bild noch mal für den Spezialfall der Generation per Licht in indirekten
Halbleitern an. Dabei beachten wir, daß, was immer auch passiert, der Energie- und
der Impulserhaltungssatz immer befriedigt werden. Ersteren haben wir schon mehrfach
bemüht, letzteren noch nicht. |
|
|
|
|
 |
Bei der Generation im obigen Beispiel ist der Energierhaltungssatz befriedigt, wenn das Photon
mindestens die Energie der Bandlücke Eg mitbringt. Der Impulserhaltungssatz ist auch ohne
Probleme machbar (müssen wir einfach glauben). Das gilt bei der Generation sowohl für direkte
als auch für indirekte Halbleiter. |
|
 |
Bei der Rekombination kommt der große Unterschied. In direkten
Halbleitern kann sie problemlos erfolgen, sobald ein Elektron am selben Ort auf ein Loch trifft. Die Energie geht in die
Erzeugung eines Photons, und der Impulshaltungssatz macht keine Probleme – im Gegensatz zu den indirekten Halbleitern! |
|
 |
Wenn in einem indirekten Halbleiter ein Junge auf ein
Mädchen trifft... sorry: ein Elektron auf ein Loch – passiert gar nichts! Bei einer Rekombination würde
der Impulserhaltungssatz verletzt werden, und das geht nicht, also passiert nichts. |
|
 |
Die beiden brauchen einen Vermittler, einen dritten Partner, der auch Impuls aufnehmen kann.
Das sind Defekte mit Zuständen im Bandgap. Die Rekombination findet dann schematisch so wie eingezeichnet statt. |
|
 |
Damit ist die Rekombination schwierig. Die Teilchen müssen lange wandern, bis sie am
selben Ort ein Gegenteilchen und den dritten Partner
finden. Lebensdauer und Diffusionslänge sind groß; Licht kommt keines raus. |
 |
Wie groß oder klein genau sind denn
L
und t? Das ist eine der "guten" Fragen, die nicht so leicht zu beantworten
sind. Wer sich traut, schaut via Link in eine Vorlesung
für Fortgeschrittene, der Rest (und die Mutigen) merkt sich nur einen einzigen
Zusammenhang: |
|
 |
Die Lebensdauer in indirekten Halbleitern, inbesondere
also in Silizium, ist extrem sensitiv auf Kristallgitterdefekte, insbesondere auf atomare Fehlstellen. Wir schauen uns das an einem Beispiel an (die rote Kurve bezieht sich natürlich
auf p-Si): |
| |
|
 |
Die Lebensdauer verringert sich linear mit der Goldkonzentration. Selbst bei der
kleinen Konzentration von 1014 cm –3 (» 2
ppb)
beträgt sie nur 1 µs. Bis zu einer Lebendauer von 1 ms wie oben angegeben fehlen noch drei Größenordnungen
– die Goldkonzentration müßte also bei 2 ppt liegen, um die Millisekunde zu erreichen. |
|
 |
So ist es auch! "Life time killer " wie Gold
(und viele andere metallische Fremdatome, am schlimmsten Fe, Ni, Cu, Ti) sind allesamt "tiefe Störstellen" mit Energieniveaus für Elektronen, die tief in der
Bandlücke liegen (d. h. in etwa in der Mitte; "tief" wird hier im Unterschied zu "flach" verwendet,
was sich auf die typischen Dotierniveaus bezieht). Der Halbleitertechnologe fürchtet sie wie der Teufel das Weihwasser!
|
|
 |
An dieser Stelle liegt eine der Wurzeln der extremen Reinheits- und Perfektionsanforderungen
der Si-Technologie. Kristalle
verschmutzen gern (bei höherer Temperatur). Der Kampf für Reinheit ist deshalb immer ein Kampf gegen die Entropie – und das kostet Energie (und vor allem viel Geld).
|
|
 |
Hier steckt auch das Grundproblem der Si-Solarik: Gute Solarzellen kann man nur aus
Si mit möglichst großer Diffusionslänge und damit Lebensdauer machen. Und diese Sorte Si
kann einfach nicht beliebig billig sein! |
| |
|
© H. Föll (MaWi für ET&IT - Script)